Необходимое время: 4 часа
Теоретическая часть.
Архитектура карты Кохонена (SOM)
Архитектура карты Кохонена (Self-Organization Map) основана на создании системы нейронов связанных с общими входами. Цель этой формы нейронных сетей – организовать качественную кластеризацию образов при обучении без учителя. Структура сети приведена на Рис. 1
 |
Рис. 1. Архитектура карты Кохонена.
В данном случае нейроны первого слоя связаны между собой связями, влияющими на процедуру обучения (на рис. 1 пунктирная линия) и реализуют радиально-базисную функцию активации.
Обучение без учителя.
Обучение по соревнованию.
Слой 0 – рецептивный.
Число входов 
, число выходов совпадает с числом нейронов слоя 1.
Сеть прямого распространения.
Нейрон – Кохонена (RBF)
Обучение SOM.
1. Процедура обучения начинается с инициализации нейронов карты Кохонена. Возможны разные варианты инициализации: нулевого состояния нейронов в скрытом слое.
2. Алгоритм обучения основан на том, что из всего слоя выбирается нейрон, значения синапсов которого максимально походят на входной образ, и подстройка весов по формуле (1) проводится для него и его ближайших соседей.
Подстройку синапсов проводят на основании их значений от предыдущей итерации.
,
,
-степень соседства с победителем соревнования (см. Рис.1),
- скорость обучения 
.(1)
Из (1) видно, что обучение сводится к минимизации разницы между входными сигналами нейрона, поступающими с выходов нейронов предыдущего слоя 
(нейроны рецептивного слоя), и весовыми коэффициентами его синапсов.
Выбор нейрона победителя может осуществляться, например, расчетом скалярного произведения вектора весовых коэффициентов с вектором входных значений. Максимальное произведение дает выигравший нейрон.
Другой вариант – расчет расстояния между этими векторами в 
-мерном пространстве, где – размер векторов.
. (2)
где 
– индекс нейрона в слое , 
– индекс суммирования по нейронам слоя (
), 
– вес синапса, соединяющего нейроны; выходы нейронов рецептивного слоя.
В данном случае, "побеждает" нейрон с наименьшим расстоянием. Иногда слишком часто получающие активность нейроны принудительно исключаются из рассмотрения, чтобы "уравнять права" всех нейронов слоя. Простейший вариант такого алгоритма заключается в торможении только что выигравшего нейрона.
3. Обучение заканчивается, когда на обучающей выборке обеспечена стабилизация положения нейронов или пройдено заданное количество эпох.
Практическая часть.
Функции для организации и обучения SOM.
Для построения сети саморганизующаяся карта Кохонена (SОМ) воспользуемся возможностями, предоставляемыми пакетом прикладных программ Neural Network Toolbox, входящим в состав математического пакета Matlab. Создание и обучение сети SОМ осуществляется функцией
net = newsom(PR,[d1,d2,...],tfcn,dfcn)
newsom([<диапазон 1-го входа>; <…>;<диапазон n-го входа>;],[<число нейронов по Х> <число рядов по Y>], <сетка связей по умолчанию hextop>, <функция дистанции между нейронами>)
Пример:
net = newsom([0 2; 0 1],[3 5]); % карта кохонена из 15 нейронов
Построим топологию двумерной карты Кохонена
plotsom(net.layers{1}.positions) % отображение сети соседей карты Кохонена.
Процедура обучения реализуется следующим образом.
net.trainparam.epochs = <число эпох обучения>;
% обучение сети
net = train(<имя сети>,<имя массива примеров>);
Построим карту дистанции между нейронами двумерной карты Кохонена
plotsom(net.iw{1,1},net.layers{1}.distances)
Промоделируем обученную карту Кохонена на массиве векторов входа
a = sim(net,P);
Нейроны сети Кохоннена можно объединять в разные сети латеральных связей. В Matlab для решения этого вопроса используют функции gridtop (четырехугольная), hextop(шестисвязная), randtop(случайная).
· GRIDTOP
Рассчитать положения нейронов на 4-мерной сетке с прямоугольной топологией размера 5x4x3x2 и выполнить попытку построить график
pos = gridtop(5,4,3,2);
figure(1), clf, plotsom(pos), plotsom(pos)
· HEXTOP
Рассчитать положения нейронов на 3-мерной сетке с гексагональной топологией размера 5x4x3 с 60 нейронами и построить график их расположения
pos = hextop(5,4,3);
figure(1), clf, plotsom(pos), plotsom(pos)
· RANDTOP
Рассчитать положения нейронов на 3-мерной сетке с гексагональной топологией размера 5x4x3 с 60 нейронами и построить график их расположения
pos = randtop(5,4,3);
figure(1), clf, plotsom(pos), plotsom(pos)
Пример формирования SOM.
Создать сеть
net = newsom([0 2; 0 2; 0 1], [4 5]);
N=100;
Создаем выборку их 2*N точек для 2-х центров (0.5 0.5 0.5) и (0.9 1.5 1.5)
x1=normrnd(.5,0.25,1,N);
y1=normrnd(.5,0.25,1,N);
z1=normrnd(.5,0.25,1,N);
x2=normrnd(.9,0.25,1,N);
y2=normrnd(1.5,0.25,1,N);
z2=normrnd(1.5,0.25,1,N);
P = [x1 x2; y1 y2; z1 z2];
Выводим точки обучающей выборки:
plot3(P(1,1:N),P(2,1:N),P(3,1:N),'.g');
hold on
plot3(P(1,N+1:2*N),P(2,N+1:2*N),P(3,N+1:2*N),'ok');
Проводим тренировку сети:
net.trainParam.goal=0.001;
net=train(net,P);
Выводим координаты нейронов
plotsom(net.iw{1,1},net.layers{1}.distances)
Y=sim(net,P);
– содержит реакции всех нейронов на все примеры. Размер 
составляет 
-строк (строка соответствует реакциям нейрона на n образов) и 
-столбцов (каждому столбцу соответствуют реакции на него нейронов).
Ошибка разделения при обучении можно определить как число нейронов опознающих оба класса примеров к общему числу нейронов. Для этого необходимо зафиксировать, на какой класс объектов реагирует каждый нейрон. Этот этап можно назвать раскраской карты.
Задание 1.
Использовать пример из somm12.m
close all;
X = [0 1; 0 1]; % Cluster centers to be in these bounds.
clusters = 3; % This many clusters.
points = 50; % Number of points in each cluster.
std_dev = 0.05; % Standard deviation of each cluster.
P = nngenc(X,clusters,points,std_dev);
% Plot P.
figure(1);
plot(P(1,:),P(2,:),'+r');
hold on;
%число рядов и нейронов в ряду для сетки связей
n1=3;m1=3;
net = newsom([0 1;0 1],[n1 m1]);
w = net.IW{1};
plot(P(1,:),P(2,:),'og');
net.trainParam.epochs = 100;
net = train(net,P);
w = net.IW{1};
hold on;
plot(w(:,1),w(:,2),'ob');
hold on;
plotsom(net.iw{1,1},net.layers{1}.distances);
figure(2);
plotsom(net.layers{1}.positions);
%net test
Y=sim(net,P);
Y1=full(Y);
Neur=[]
for i=1:clusters
Neur_j=[zeros(1,n1*m1)];%все нейроны кластера i пока не активны
for j=1:points
b=Y1(:,(i-1)*points+j);
%активные нейроны
k=find(b==1);
Neur_j(k)=1;
end
Neur=[Neur; Neur_j];
end
%столбец g Neur соответствует реакциям нейрона g на объекты кластеров от
%1-го до clasters. Если в столбце больше одной 1, то нейрон реагирует более
%чем на один кластер (т.е. смешаный нейрон - плохой). Если нейрон не имеет
%ни одной реакции на объекты, то он "мертвый", т.е. плохой нейрон. Чем меньше плохих
%нейронов, тем лучше обучение.
Neur
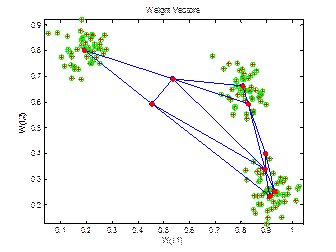
Рис. 1 результат работы скрипта.
Neur =
1 1 0 0 1 1 1 0 1
1 1 1 0 1 1 1 0 1
1 1 0 0 1 1 1 0 1
Все нейроны плохие кроме 3-го.
Оценить число нейронов реагирующих на объекты одного класса для сетей разного размера
| Число рядов n1 | Число нейронов в ряду m1 | Число плохих нейронов по отношению к n1*m1 (общему числу нейронов) |
Практическая часть