Структура системных рисков

Впервые исследование структуры рисков провел американский ученый Г. Марковиц[18], который известен как разработчик портфельной теории, благодаря которой стало возможным широкое применение диверсификации как инструмента управления рисками. Исследование рисков он осуществил опосредованно через исследование доходности финансовых активов компаний. Он выделяет систематический риск (sistematic risk) и определяет его как риск, «который не элиминируется диверсификацией активов рыночного портфеля полностью», в своей базовой работе «Portfolio selection», которая была опубликована в 1952 году.

Дж. К. Ван Хорн[19] также выделяет систематический риск – риск по акции, связанный с колебаниями ситуации на рынке ценных бумаг. Этот риск не может быть устранен посредством диверсификации. Он измеряется значением коэффициента β для данной ценной бумаги. Далее он использует выражение «неизбежный риск». Он отмечает, что величина этого риска зависит от таких факторов, как изменения в экономике и политике, налоговые реформы, оказывающие воздействие на стоимость всех акций. Состав общего риска рыночного портфеля активов представлен на рис. 1.6.

Брейли и Майерс отмечают, что рыночные риски, систематические риски или недиверсифицируемые риски – это одно и то же[20]. Они отмечают, что рыночные (систематические риски) связаны с рисками общеэкономического характера, которым подвержен любой бизнес. «Именно поэтому существует тенденция одновременного изменения цен на акции. И по этой же причине инвесторы страдают от «рыночной неопределенности».

Данные исследователи определили факторы, влияющие на величину систематических (системных) рисков, как факторы общеэкономического характера.

Данные исследователи определили факторы, влияющие на величину систематических (системных) рисков, как факторы общеэкономического характера.

 

 

Рис. 1.6. Общий, несистематический и систематический риск[21]

 

Величину систематических рисков в экономике определяют посредством выявления вознаграждения за риски, которое считают достаточным для себя большинство инвесторов, обладающих хорошо диверсифицированными портфелями (рыночная норма доходности). Чем выше уровень изменчивости дохода на акции в экономике, тем выше уровень систематических рисков. Значит, на уровень рисков влияет и спо-собность государственной системы страховать риски. Например, развитая система финансовых институтов (банков, страховых компаний и инвестиционных фондов) способствует снижению систематических рисков. В современной регулируемой экономике эта способность системы приобретает особенно большое значение для предприятий, и исследуемые нами риски целесообразно назвать системными, т.е. порожденными макросистемой организации бизнеса. Это тем более актуально, что понятие «систематический риск» в сознании прочно связано с рынком ценных бумаг, так же, как понятие «рыночный риск».

Таким образом, уровень системных рисков предприятий – так же варьируемая величина, и зависит он как от структуры системных рисков, так и от степени влияния составляющих системных рисков на дивер-сифицированные компании.

Начало современным трактовкам состава системных рисков было положено Г. Марковицем[22], лауреатом Нобелевской премии 1990 года (хотя сами работы были опубликованы, как упоминалось выше, еще в 50-е гг. ХХ в.).

В основе выводов Г. Марковица лежат исследования поведения участников экономических отношений при выборе оптимальных инвестиционных решений на фондовом рынке. Принимая решение о вложениях в ценные бумаги, участники фондового рынка должны иметь в виду то обстоятельство, что доходность ценных бумаг и, таким образом, доходность формируемого портфеля в предстоящий период владения неизвестны. Значит, уровень доходности является случайной переменной, которая имеет свои характеристики, одна из которых – ожидаемое, или среднее значение доходности, а другая – стандартное отклонение как мера риска. Таким образом, участники экономических отношений на фондовом рынке стремятся максимизировать ожидаемую доходность и миними-зировать неопределенность, т.е. риск.

Используя теоретический подход Г. Марковица к анализу взаимосвязи между доходностью и риском, а также информацию о поведении и содержании интересов участников экономических отношений на фондовом рынке, возможно адекватно учесть обе эти цели, противоречащие друг другу.

Теоретический метод Г. Марковица базируется на кривых безразличия. Эти кривые используются для характеристики поведения участников экономических отношений на фондовом рынке в плоскости «доходность – риск». При этом важным свойством кривых безразличия является то, что все портфели, лежащие на одной заданной кривой безразличия, являются равноценными для участников экономических отношений на фондовом рынке.

Имеется бесконечное число кривых безразличия, и считается, что любой портфель, лежащий на кривой безразличия выше и левее, более привлекателен, чем портфели, лежащие ниже и правее.

При данных предпосылках ожидаемая доходность портфеля, состоящая из N ценных бумаг, будет определяться как

 

(1.1)

 

где r_p – ожидаемая доходность портфеля; X_i – доля начальной стоимости портфеля, инвестированная в ценную бумагу i; r_i, – ожидаемая доходность ценной бумаги i; N – количество ценных бумаг в портфеле.

 

Вклад каждой ценной бумаги в ожидаемую доходность портфеля зависит от ее ожидаемой доходности, а также от доли начальной стоимости портфеля, вложенной в данную ценную бумагу. Другие факторы значения не имеют.

На рис. 1.7 проиллюстровано положение достижимого множества, представляющего собой все портфели, которые могут быть сформированы из группы N ценных бумаг и удовлетворяющие интересам участников экономических отношений на фондовом рынке, т.е. множество портфелей, обеспечивающих минимальный риск при изменяющемся уровне ожидаемой доходности. На рис. 1.7, а это часть левой границы достижимого множества, расположенная между точками S u G.

Теория об эффективном множестве утверждает, что участники экономических отношений на фондовом рынке выберут свой оптимальный портфель ценных бумаг из множества портфелей, каждый из которых, во-первых,обеспечивает максимальную ожидаемую доходность для некоторого уровня риска и, во-вторых,минимизирует риск для некоторого значения ожидаемой доходности. С учетом этих условий участников экономических отношений на фондовом рынке будут удовлетворять только те портфели, которые располагаются на верхней и левой границе достижимого множества между точками Е и S. Эти портфели составляют множество эффективных портфелей, и из них будет выбираться оптимальный.

Для выбора оптимального портфеля участники фондового рынка должны совместить свои кривые безразличия с эффективным множеством (см. рис. 1.7, б). Оптимальный портфель будет соответствовать точке, в которой кривая безразличия касается эффективного множества. Таким портфелем является портфель О* на кривой безразличия I ₂.

 

а

 

б

 

Рис. 1.7. Проведение участников экономических отношений

на фондовом рынке в плоскости «доходность – риск»

Таким образом, с методологической точки зрения, теорию Г. Марковица можно определить как практически-нормативную, позволяющую определить некоторые объективные нормы для выявления величины и структуры рисков. Основные теоретические положения Марковица можно сформулировать следующим образом:

1. Совокупность рисков на фондовом рынке можно разложить на две составные части. Во-первых, это недиверсифицируемый риск, которому подвержены все вложения в ценные бумаги и который нельзя исключить. Во-вторых, специфический риск, характеризующий риск вложений в каждую конкретную ценную бумагу, можно минимизировать путем диверсификации вложений.

2. При помощи разработанного метода критических линий можно выделить неперспективные вложения в ценные бумаги, т.е. не удов-летворяющие введенным ограничениям. В результате мы можем получить только эффективные портфели ценных бумаг, содержащие минимальный риск при заданном доходе. Риски, присущие именно этим портфелям, и будут являться системными.

Таким образом, структура системных рисков зависит от практической ситуации в экономической системе и, в частности, от степени диверсификации фондов предприятий. Это позволяет на практике использовать обычные индексы фондовых рынков, например, «Доу Джонсона», «Стэндарт энд пурс 500», в России – РТС, при операциях с обыкновенными акциями.

В конце 50-х годов другой Нобелевский лауреат – Дж. Тобин – развил портфельный подход Г. Марковица, аналитически обосновав концепцию безрискового предоставления и получения займов[23].

В своей модели Марковиц исходил из того, что активы, обращающиеся на фондовом рынке, в отдельности являются рискованными, т.е. каждый из N рискованных активов дает неопределенный доход за период его владения. Всвою очередь, Дж. Тобин, на наш взгляд, дал более широкую трактовку модели Марковица. Во-первых, участники экономических отношений на фондовом рынке могут инвестировать не только в рискованные, но и в безрисковые активы. По существу, это означает, что теперь имеется N активов, доступных для инвестиций, включая (N –1) рискованный актив и один безрисковый. Во-вторых, участники экономических отношений могут одалживать деньги при обязательных выплатах по определенной процентной ставке по взятым займам. Кроме того, рассматривается эффект от добавления безрискового актива к набору рискованных активов.

Поскольку все корпоративные ценные бумаги имеют некоторую вероятность неуплаты, то безрисковый актив не может быть выпущен корпорацией. Таким образом, безрисковым активом могут быть исклю-чительно государственные ценные бумаги.

Теперь эффективное множество состоит из прямого отрезка r_f T и искривленного отрезка ТВ, где r_f – безрисковая ставка.

При кривой безразличия I ₁ (рис. 1.8) оптимальный портфель O_i состоит из инвестиций в безрисковый актив и в портфель Т. Если же участники экономических отношений на фондовом рынке менее склонны избегать риска, то кривая безразличия будет I ₁ а оптимальный портфель будет состоять из получения займа по безрисковой ставке и из инвестиции этих и собственных фондов в портфель Т.

 

 

Рис. 1.8. Формирование оптимального портфеля финансовых активов

 

В первой половине 60-х годов профессором Стендфордского университа У. Шарпом,была предложена рыночная (индексная) модель[24], которая использовалась для оценки соотношения доходности обыкновенных акций предприятий и акций, учитываемых в любом ведущем индексе биржевых котировок, например «S&P-500» («Стандарт энд пурс 500»).

Суть рыночной (индексной) модели можно представить как

 

, (1.2)

 

где r_t – доходность ценной бумаги i за данный период; r_t – доходность на рыночный индекс J зa этот же период; α _it – коэффициент смещения; β _it – коэффициент наклона; ε _it – случайная погрешность.

Случайная погрешность показывает, что рыночная модель не очень точно объясняет доходность ценных бумаг. Без учета случайной погрешности формула (1.2) представляет собой уравнение прямой линии, называемой графиком рыночной модели для отдельной ценной бумаги. Коэффициент β – это коэффициент наклона рыночной модели, вычисляемый следующим образом:

 

, (1.3)

 

где – обозначает ковариацию между доходностью акции i и доходностью на рыночный индекс, а –обозначает дисперсию доходности на индекс.

Общий риск ценной бумаги i, измеряемый ее дисперсией и обозначаемый как , исходя из рыночной модели, слагается из двух компонентов: рыночного риска и собственного риска. Таким образом, равняется следующему выражению:

 

, (1.4)

 

где – дисперсия доходности на рыночный индекс; – рыночный риск ценной бумаги i, a 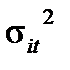– собственный риск ценной бумаги i, мерой которого является дисперсия случайной погрешности из формулы 1.2.

Если долю средств, вложенных в ценную бумагу i данного портфеля р, обозначить через X _i, то доходность портфеля может быть вычислена по следующей формуле:

 

. (1.5)

Подставляя r_i из формулы (1.2) в формулу (1.5), получим следующую рыночную модель портфеля:

 

(1.6)

, (1.7)

, (1.8)

. (1.9)

 

Ранее, исходя из факторной (индексной) рыночной модели ценной бумаги (1.2), было получено выражение для риска ценной бумаги (1.3). По аналогии из уравнения рыночной модели портфеля (1.6) следует, что общий риск портфеля, измеряемый дисперсией его доходности и обозначенный , выражается следующей формулой:

 

, (1.10)

 

где определяется по формуле (1.3).

Формула (1.10) показывает, что общий риск портфеля состоит из двух компонентов, аналогично двум компонентам общего риска отдельных ценных бумаг. Эти компоненты носят также название рыночного риска и собственного риска .

 

 

Предполагая, что случайные отклонения доходности ценных бумаг являются некоррелированными, получаем

 

. (1.11)

 

Если во все ценные бумаги вложено одинаковое количество средств, то доля X составит 1/ N, а уровень собственного риска, как это показано в формуле (1.11), будет следующим:

 

. (1.12)

 

Значение, находящееся внутри квадратных скобок, является средним собственным риском ценных бумаг, образующих портфель. Но собственный риск портфеля в N раз меньше данного значения, так как находится вне квадратных скобок. Если количество бумаг в портфеле становится больше, то величина 1/ N уменьшается, что приводит к уменьшению собственного риска портфеля.

Таким образом, участники экономических отношений на фондовом рынке при формировании оптимального портфеля должны учитывать важнейшее значение диверсификации, под которым имеется в виду включение в него нескольких финансовых инструментов с различными характеристиками.

Поэтому с полным основанием можно сделать следующее заключение: диверсификация существенно уменьшает собственный риск. На рис. 1.9 показано, как диверсификация приводит к снижению собственное риска и усреднению рыночного риска.

 

 

Рис. 1.9. Влияние диверсификации на структуру и уровень рисков

При включении в портфель большого числа ценных бумаг собственный риск, называемый также диверсифицируемым риском, может быть практически сведен к нулю, в противном случае реальный риск портфеля будет представлен неустранимым риском. Диверсифицируемый риск может быть в принципе устранен, даже если эти активы выбраны случайно. Важным обстоятельством является то, что хотя риск сокращается посредством диверсификации, этот процесс не воздействует на доходность ценной бумаги. Иными словами, доход, приносимый данной ценной бумагой, не зависит от того, находится ли она в портфеле или отдельно, т.е. риск может сокращаться с помощью диверсификации портфеля без всякого ущерба для доходности данного актива.

Практически одновременно с У. Шарп другой ученый Дж. Линтнер разработал модель оценки финансовых активов[25](САРМ – «capital asset pricing model»). В рамках этой модели было проанализировано коллективное поведение на фондовом рынке и выявлен характер конечной равновесной зависимости между риском и доходностью каждой ценной бумаги.

 

 

В общих чертах модель Шарпа–Линтнера исходит из того, что:

1. Участники экономических отношений производят оценку инвестиционных портфелей, основываясь на ожидаемых доходностях и их стандартных отклонениях за период владения. Участники экономических отношений при выборе между двумя портфелями предпочтут тот, который при прочих равных условиях дает наибольшую ожидаемую доходность. Участники экономических отношений не желают рисковать. Они предпочтут портфель с наименьшим стандартным отклоненинием. Частные активы бесконечно делимы. При желании можно купить часть акций.

2. Существует безрисковая процентная ставка, гарантированная государством. Для всех участников экономических отношений период вложения одинаков. Безрисковая процентная ставка так же одинакова для всех. Информация свободно и незамедлительно доступна для всех участников экономических отношений на фондовом рынке.

3. Участники экономических отношений имеют однородные ожидания, т.е. они одинаково оценивают ожидаемые доходности, среднеквадратические отклонения и ковариации доходностей ценных бумаг.

При этих допущениях в равновесном случае все участники экономических отношений выбирают один и тот же «касательный» портфель, обозначенный на рис. 1.10 через Т.

 

Рис. 1.10. Формирование рыночного портфеля ценных бумаг

В результате мы получим рыночный портфель, состоящий из всех ценных бумаг, в котором доля каждой соответствует ее относительной рыночной стоимости, равной ее совокупной рыночной стоимости, деленной на сумму совокупных рыночных стоимостей всех ценных бумаг. В таком случае становится правомерным определить «касательный» портфель как рыночный и обозначить его через М (market) вместо Т.

Приведенные исследования экономистов структуры совокупности недиверсифицируемых рисков экономики дают нам ключ к анализу и управлению системных рисков предприятия. Автор считает целесообразным использовать стоимостной подход в управлении системными рисками.

Стоимость капитала предприятия, определяемая на основе дисконтирования денежного потока, включает информацию о рисках предприятия в сам процесс и позволяет проводить диагностику деятельности предприятия в системе «риск–доход».

Анализ информации о рыночной оценке предприятия показывает, что уровень совокупного риска предприятия, выраженный ставкой дисконтирования, имеет выраженную тенденцию роста.

Тенденция роста уровня рисков отечественных предприятий наиболее ярко проявилась в 2003–2006 годах. Это связано со снижением ставки рефинансирования в этот период как попытки государства снизить общеэкономический риск. В работе проведен анализ динамики нормы дисконта, применяемой при рыночной оценке капитала предприятий в 2003–2006 годах.