Каспийский общественный университет
Кафедра «Автоматизации и Вычеслительной техники»

Задание по СРСП №5
Тема: «Мгновенный центр ускорений (МЦУ) »
«Сложное движение точки »
«Определение скоростей и ускорений точек в сложном движении »
Выполнил: Студент НГД12(б)-2р Калиев А.О
Проверила: Проф. Кафедры АиВТ Шегенова Ж.Б
Алматы 2013 г
Мгновенный центр ускорений (МЦУ)
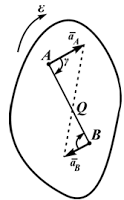
В учебной литературе доказывается, что при движении фигуры в плоскости в каждый момент времени существует такая точка плоской фигуры, ускорение которой в этот момент равно нулю. Эту точку называют мгновенным центром ускорений (МЦУ). В наших рассуждениях будем обозначать её буквой Q.
Взяв эту точку за полюс, получим формулу для определения ускорения произвольной точки:

или

Угол, который составляет вектор ускорения точки M с линией MQ, определится из соотношения:

То есть у всех точек плоской фигуры этот угол одинаков. Из рисунка 2.23 видно, что мгновенный центр ускорений лежит в точке пересечения линий, составляющих угол γ с соответствующими ускорениями точек.

Рисунок 2.23
На рисунках 2.24-2.26 приведены частные случаи определения положения мгновенного центра ускорений.


а б
V0-const, ω=V0/R, ε=0, ε=0, ω≠0,
tqγ=0, γ=0, tqγ= ε/ω2/0,
aA=aB=aD=aCv=ω2R=V20/R, γ=0o,
т. O - МЦУ aA=ω2⋅AQ,
aB=ω2⋅BQ
Рисунок 2.24

а б


Рисунок 2.25


а б
ε≠0, ω=0, tqγ=ε/ω2=∞, ε≠0, ω=0, tqγ=ε/ω2=∞
γ=90o, γ=90o,
aA=ε⋅AQ, aB=ε⋅AQ aA=ε⋅AQ, aB=ε⋅AQ
Сложное движение точки
Законы Ньютона сформулированы для движения точки по отношению к инерциальным системам отсчета. Для определения кинематических параметров точки при движении относительно произвольно движущейся системы отсчета вводится теория сложного движения.
Сложным называют движение точки по отношению к двум или нескольким системам отсчета.

Рисунок 3.1
На рисунке 3.1 показаны:
- условно принимаемая за неподвижную система отсчета O1x1y1z1;
- движущаяся относительно неподвижной система отсчета Oxyz;
- точка M, перемещающаяся по отношению к подвижной системе отсчета.
Движение точки M в данном случае является сложным. Её движение по отношению к подвижной системе отсчета называют относительным движением.
Движение той точки подвижной системы отсчета, в которой в данный момент находится движущаяся точка, по отношению к неподвижной системе отсчета называют переносным движением. Движение точки M по отношению к неподвижной системе отсчета называют абсолютным движением.
По аналогии с этими определениями будут называться относительные, переносные и абсолютные скорости и ускорения точки. Для их обозначения в относительном движении часто всего используется индекс r (relative – относительный) - Vr, ar; в переносном движении индекс e (entrained - увлекать за собой) - Ve, ae.
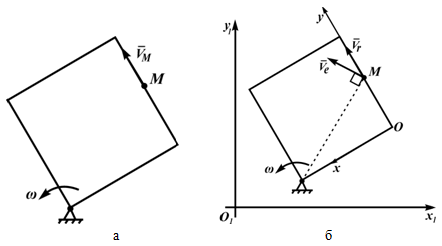
Рисунок 3.2
Ниже приведен пример сложного движения точки - M.
На рисунке 3.2,а показан квадрат, вращающийся в плоскости чертежа вокруг неподвижной точки. По стороне квадрата движется точка M. Она участвует в двух движениях, поэтому можно ввести две системы отсчета: неподвижную, например, O1x1y1z1 - по отношению к которой вращается квадрат и подвижную Oxyz, скрепленную с квадратом, по оси Oy которой движется точка M (рисунок 3.2,б).
Движение точки M по стороне квадрата (по оси Oy скрепленной с квадратом подвижной системы) является относительным - скорость в этом движении Vr. Вращение точки M вместе с квадратом - переносное движение, скорость в этом движении - Ve. Абсолютное движение является результатом сложения переносного и относительного движений.
Определение скоростей и ускорений точек в сложном движении
Теоремы о скоростях и ускорениях точек в сложном движении изложены во всех учебниках по теоретической механике.
Абсолютная скорость точки определяется как геометрическая сумма переносной и относительной скоростей:

Каждое слагаемое в этой формуле определяется независимо друг от друга, исходя из соответствующего закона движения. В примере на рисунке 3.2 относительная скорость Vr определяется с учетом закона движения точки по оси Oy.
Переносная скорость определится как скорость точки M при вращении вместе с квадратом вокруг оси его вращения. Величина абсолютной скорости может быть определена с помощью теоремы косинусов:

Для определения вектора абсолютной скорости можно равенство (3.1) спроецировать на выбранные оси координат, найти проекции абсолютной скорости, её величину и направляющие косинусы, то есть определить углы, которые вектор скорости составляет с выбранными осями.
Ускорение точки определяется как сума трех ускорений: переносного, относительного и кориолисова (поворотного):

Первые два слагаемые этой формулы определяются из соответствующих законов переносного и относительного движений. В случае неравномерных криволинейных движений эта формула имеет вид

Кориолисово ускорение определяется по формуле:

Величина этого ускорения aK=2ωeVrsinα, (3.5)
где α - угол между векторами переносной угловой и линейной относительной скоростями.
Направление кориолисова ускорения определяется двумя правилами: