Комплект примерных билетов по геометрии для выпускников 9 классов

Билет №1

1. Углы, образованные при пересечении двух параллельных прямых третьей прямой. Свойство внутренних односторонних углов.

2. Треугольник: определение и виды. Теорема косинусов (доказательство). Следствия из теоремы косинусов.

3. Найдите диагонали равнобедренной трапеции, основания которой равны 4 см и 6 см, а боковая сторона равно 5 см.

4. В окружности радиуса 6 см проведена хорда АВ. Через середину М этой хорды проходит прямая, пересекающая окружность в точках С и Е. Известно, что СМ = 9 см, = .

Найдите длину отрезка СЕ.

Билет №2

1. Вертикальные углы: определение и свойство.

2. Треугольник: определение и виды. Теорема синусов (доказательство). Следствия из теоремы синусов.

3. Углы ADC и ABC вписаны в окружность. Какой может быть величина угла ADC, если известно, что ?

4. Дана прямоугольная трапеция ABCD (AD – большее основание, AB AD). Площадь трапеции равна см , . Найдите диагональ AC.

Билет №3

1. Смежные углы: определение и свойства.

2. Прямоугольный треугольник. Теорема Пифагора (доказательство).

3. Найдите площадь круга, если длина окружности равна см.

4. Площадь параллелограмма равна см , ,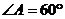AB:AD = 10: 3. Биссектриса угла А пересекает сторону параллелограмма в точке М. Найдите длину отрезка АМ.

Билет №4

1. Треугольник: определение и виды. Равные треугольники (определение). Признаки равенства треугольников.

2. Теорема Фалеса (доказательство).

3. Величины углов ABC и KBC относятся как 7:3, а их разность равна . Могут ли эти углы быть смежными?

4. Найдите радиус окружности, вписанной в параллелограмм, если его диагонали равны 12 см и .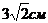

Билет №5

1. Параллелограмм: определение и признаки.

2. Окружность, описанная около треугольника. Теорема о центре окружности, описанной около треугольника (доказательство).

3. В равностороннем треугольнике ABC проведена высота BD. Найдите углы треугольника ABD.

4. Найдите диагональ правильного восьмиугольника , если площадь треугольника равна м.

Билет №6

1. Параллелограмм: определение и свойства.

2. Окружность, вписанная в треугольник. Теорема о центре окружности, вписанной в треугольник (доказательство).

3. В остроугольном равнобедренном треугольнике угол между основанием и высотой, проведенной к боковой стороне, равен . Найдите углы этого треугольника.

4. Диагонали трапеции ABMK пересекаются в точке О. Основания трапеции BM и AK относятся соответственно как 2: 3. Найдите площадь трапеции, если известно, что площадь треугольника AOB равна 12 см .

Билет №7

1. Прямоугольник: определение и свойства.

1. Средняя линия треугольника. Теорема о средней линии треугольника (доказательство).
2. Найдите сторону ромба, если известно, что его диагонали равны 24 см и 32 см.
3. Найдите площадь правильного многоугольника, если его внешний угол равен , а диаметр описанной около него окружности равен 8 см.

Билет №8

1. Прямоугольник: определение и признаки.

2. Равнобедренный треугольник. Свойство медианы равнобедренного треугольника, проведенной к основанию (доказательство).

3. Найдите катеты прямоугольного треугольника, если известно, что его гипотенуза равна см, а один из острых углов в два раза больше другого.

4. К окружности проведены касательные МА и МВ (А и В – точки касания). Найдите длину хорды АВ, если радиус окружности 20 см, а расстояние от точки М до хорды АВ равно 9 см.

Билет №9

1. Ромб: определение и признаки.
2. Треугольник: определение и виды. Теорема о сумме углов треугольника (доказательство).
3. Найдите длину окружности, если известно, что площадь круга равна см .
4. Найдите радиус окружности, вписанной в треугольник BCD, если она касается стороны BC в точке P и известно, что BD = BC = 15 см, CP = 12 см.

Билет №10

1. Внешний угол треугольника: определение и свойство.
2. Трапеция: определение и виды. Вывод формулы площади трапеции.
3. Найдите число сторон выпуклого многоугольника, сумма внутренних углов которого равна
4. В остроугольном треугольнике ABC угол A равен , ВС = 10см, отрезки BM и CK – высоты. Найдите длину отрезка KM.

Билет №11

1. Подобные треугольники (определение). Признаки подобия треугольников.
2. Теорема о сумме углов выпуклого n-углольника (доказательство).
3. Найдите медиану, проведенную к гипотенузе прямоугольного треугольника, если известно, что его катеты равны 8 см и 6 см.
4. Найдите радиус окружности описанной около трапеции, если известно, что средняя линия трапеции равна 14 см, боковая сторона равна см, а одно из оснований трапеции является диаметром описанной окружности.

Билет №12

1. Медиана, биссектриса и высота треугольника: определения и свойства.
2. Правильный многоугольник. Вывод формулы для нахождения радиуса окружности, описанной около правильного n – угольника.
3. В прямоугольный треугольник вписана окружность радиуса 4 см. Найдите периметр этого треугольника, если известно, что его гипотенуза равна 26 см.
4. Две стороны параллелограмма равны 13 см и 14 см, а одна из диагоналей равна 15 см. Найдите площадь треугольника, отсекаемого от параллелограмма биссектрисой его угла.

Билет №13

1. Синус острого угла прямоугольного треугольника: определение, значения некоторых углов ( ).
2. Параллелограмм. Формулы площади параллелограмма. Вывод формулы площади параллелограмма (одной по выбору учащегося).
3. Найдите угол между векторами и , заданными своими координатами .
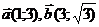4. Основание остроугольного равнобедренного треугольника равно 48 см. Найдите радиус вписанной в него окружности, если радиус описанной около него окружности равен 25 см.

Билет №14

1. Косинус острого угла прямоугольного треугольника: определение, значения некоторых углов ( ).
2. Правильный многоугольник. Вывод формулы для нахождения радиуса окружности, вписанной в правильный n-угольник.
3. Найдите стороны треугольника, периметр которого равен 5,5 см, если известно, что стороны подобного ему треугольника равны 0,4 см и 0,8 см и 1 см.
4. Найдите площадь параллелограмма KMNO, если его большая сторона равна см, диагональ MO равна 5 см, а угол MKO равен .

Билет №15

1. Тангенс острого угла прямоугольного треугольника: определение, значения некоторых углов ( ).
2. Ромб. Вывод формулы площади ромба.
3. Какие целые значения может принимать длина стороны АС треугольника ABC, если известно, что АВ = 2,9 см, ВС = 1,7 см? Ответ объясните.
4. В равнобедренную трапецию, один из углов которой равен , а площадь равна см , вписана окружность. Найдите радиус этой окружности.

Билет №16

1. Окружность (определение). Центр, радиус, диаметр окружности. Взаимное расположение окружности и прямой.
2. Формулы площади треугольника. Вывод формулы площади треугольника через две стороны и угол между ними.
3. В равностороннем треугольнике проведены две медианы. Найдите величину острого угла, образовавшегося при пересечении.
4. Средняя линия трапеции равна 15 м, сумма углов при одном из оснований равна 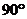. Найдите площадь трапеции, если одна боковая сторона равна м, а разность оснований равна 10 м.

Билет №17

1. Окружность (определение). Хорда окружности. Касательная к окружности: определение и свойства.
2. Трапеция. Средняя линия трапеции. Свойство средней линии трапеции (доказательство).
3. Стороны Прямоугольника равны 72 см и 8 см. Найдите сторону равновеликого ему квадрата.
4. На стороне ВС треугольника АВС отмечена точка К. Известно, что сумма углов В и С равна углу АКВ, АК = 5 м, ВК = 16 м и КС = 2 м. Найдите сторону АВ.

Билет №18

1. Понятие о геометрическом месте точек. Серединный перпендикуляр к отрезку: определение и свойство.
2. Ромб. Свойства диагоналей ромба (доказательство одного из них по выбору учащегося).
3. Средняя линия трапеции равна 8 см и делится диагональю на два отрезка, разность между которыми равна 2 см. Найдите основания трапеции.
4. В треугольнике ABC проведена медиана АМ. Найдите площадь треугольника АВС, если АС= , ВС = 10 м, 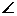МАС = .

Билет №19

1. Взаимное расположение прямых. Перпендикулярные прямые: определение и свойства.
2. Треугольник: определение и виды. Нахождение элементов треугольника по известным двум сторонам и углу.
3. Найдите углы ромба, если известно, что его периметр равен 8 см, а высота ромба равна 1 см.
4. В равнобедренную трапецию с боковой стороной, равной 10 м, вписана окружность радиуса 3 м. Найдите площадь трапеции.

Билет №20

1. Взаимное расположение прямых. Параллельные прямые: определение и свойства.
2. Треугольник: определение и виды. Нахождение элементов треугольника по известным стороне и двум углам.
3. Найдите площадь круга, описанного около правильного шестиугольника со стороной 3 см.
4. Большее основание равнобедренной трапеции равно 8 см, боковая сторона равна 9 м, а диагональ равна 11 м. Найдите меньшее основание трапеции.

Билет №21

1. Углы, образованные при пересечении двух параллельных прямых третьей прямой. Свойство внутренних накрест лежащих углов.
2. Равнобедренный треугольник. Признак равнобедренного треугольника (доказательство).
3. В окружность вписан прямоугольник, стороны которого равны 6 см и 8 см. Найдите длину этой окружности.
4. Найдите площадь параллелограмма ОМРК, если его сторона КР равна 10 м, а сторона МР, равная 6 м, составляет с диагональю МК угол, равный .

Билет №22

1. Перпендикуляр и наклонная. Расстояние от заданной точки до данной прямой.
2. Треугольник: определение и виды. Нахождение элементов треугольника по известным трем сторонам.
3. В прямоугольнике точка пересечения диагоналей удалена от меньшей стороны на 4 см дальше, чем от большей стороны. Найдите стороны прямоугольника, если известно, что его периметр равен 56 см.
4. Найдите радиус окружности, вписанной в равнобедренную трапецию, если средняя линия трапеции равна 12 м, а косинус угла при основании трапеции равен .

Билет №23

1. Вектор. Длина (модуль) вектора. Координаты вектора. Равенство векторов.
2. Круг. Площадь круга. Вывод формулы площади сектора.
3. Найдите периметр ромба, если известно, что один из углов ромба равен , а меньшая диагональ равна 5 см.
4. Площадь равнобедренного треугольника АВС с основанием ВС равна 160 м , боковая сторона равна 20 м. Высоты ВК и АН пересекаются в точке О. Найдите площадь треугольника АВО.

Билет №24

1. Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан.
2. Центральный и вписанный углы. Свойство вписанного угла окружности.
3. Найдите высоту равнобедренной трапеции, если известно, что ее основания равны 10 см и 24 см, а боковая сторона равна 25 см.
4. В треугольнике СЕН , точка Т делит сторону СЕ на отрезки СТ = 2 м и ЕТ = 14 м, . Найдите площадь треугольника СНТ.

Билет №25

1. Угол между векторами. Скалярное произведение векторов: определение и свойства.
2. Равнобедренный треугольник. Свойство углов при основании равнобедренного треугольника (доказательство).
3. Найдите площадь круга, описанного около квадрата со стороной 6 см.
4. В остроугольном треугольнике АВС на стороне АС отмечена точка М, такая, что . Найдите сторону АВ, если известно, что сторона АС = 9 м, а отрезок АМ=4м.