Вариант 1801
21. Решите неравенство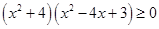 
.
Так как 
для любого х, то 
.
Ответ: 
.
Критерии оценки выполнения задания 21.
| Баллы | Критерии оценки выполнения задания |
| Неравенство решено правильно, получен верный ответ | |
| Неравенство решено правильно, но не обоснован переход к его решению
| |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
22. Из прямоугольного листа картона, размеры которого 49 см и 38 см, надо сделать коробку без крышки. Для этого по углам листа вырезают одинаковые квадраты и загибают края вверх. Чему должна быть равна сторона вырезаемого квадрата, чтобы дно коробки имело площадь 726 см2?
Пусть х см – сторона вырезаемого квадрата.
Одно из математических моделей задачи: 
.
Ответ: 8 см.
Критерии оценки выполнения задания 22.
| Баллы | Критерии оценки выполнения задания |
| Правильно составлено уравнение, получен верный ответ | |
| Правильно составлено уравнение, но при его решении допущена вычислительная ошибка, с её учётом решение доведено до ответа | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
23. Постройте график функции 
. При каких значениях k прямая 
не имеет с графиком данной функции общие точки?
, 
, 
.
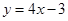Ответ: 
; 
; 
.
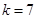Критерии оценки выполнения задания 23.
| Баллы | Критерии оценки выполнения задания |
| График построен правильно, верно указаны все значения k, при которых прямая не имеет с графиком общих точек
| |
| График построен правильно, указаны не все верные значения k | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
24. В треугольнике 
угол С равен 90°, CH ‒ высота, 
, 
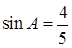. Найдите АН.
Так как 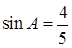, то 
, 
, 
.
, следовательно, 
, 
.
Треугольник АСН – прямоугольный. Так как 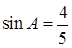, то 
, 
, 
.
, следовательно, 
, 
.
Ответ: .
Критерии оценки выполнения задания 24.
| Баллы | Критерии оценки выполнения задания |
| Получен верный обоснованный ответ | |
| При верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
25. Точки А, В, С и D принадлежат одной окружности, причем АВ пересекается с CD в точке М, лежащей внутри окружности. Докажите, что треугольники AMD и CMB подобны.
Критерии оценки выполнения задания 25.
| Баллы | Критерии оценки выполнения задания |
| Доказательство верное, все шаги обоснованы | |
| Доказательство в целом верное, но содержит неточности | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
26. Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Проведём MT параллельно AP. Тогда MT – средняя линия треугольника APC и CT = TP, а KP – средняя линия треугольника BMT и TP = BP. Обозначим площадь треугольника BKP через S. Тогда площадь треугольника KPC, имеющего ту же высоту и вдвое большее основание, равна 2 S. Значит, площадь треугольника CBK равна 3 S и равна площади треугольника CMK, которая в свою очередь равна площади треугольника AMK. Площадь треугольника ABK равна площади треугольника AMK. Итак, SBKP = S, SKPC = 2 S, SCMK = 3 S = SAMK = SABK, SKPCM = 5 S.
Значит, SABK: SKPCM =3: 5.