Метод Крамера решения систем линейных алгебраических уравнений.
Дадим ряд необходимых определений.
Система линейных уравнений называется неоднородной, если хотя бы один ее свободный член отличен от нуля, и однородной, если все ее свободные члены равны нулю.
Решением системы уравнений называется упорядоченный набор чисел, который, будучи подставленным вместо переменных в систему, обращает каждое ее уравнение в тождество.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.
Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Рассмотрим неоднородную систему линейных алгебраических уравнений, имеющую при n=m следующий общий вид:
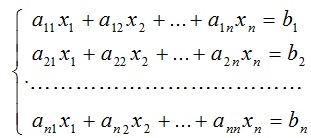 . (1.5)
Главной матрицей A системы линейных алгебраических уравнений называется матрица, составленная из коэффициентов, стоящих при неизвестных: . (1.5)
Главной матрицей A системы линейных алгебраических уравнений называется матрица, составленная из коэффициентов, стоящих при неизвестных:
 .
Определитель главной матрицы системы называется главным определителем и обозначается ∆.
Вспомогательный определитель ∆i получается из главного определителя путем замены i-го столбца на столбец свободных членов .
Определитель главной матрицы системы называется главным определителем и обозначается ∆.
Вспомогательный определитель ∆i получается из главного определителя путем замены i-го столбца на столбец свободных членов 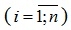 .
Теорема 1.1 (теорема Крамера). Если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, вычисляемое по формулам: .
Теорема 1.1 (теорема Крамера). Если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, вычисляемое по формулам:
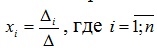 . (1.6)
Если главный определитель ∆=0, то система либо имеет бесконечное множество решений (при всех нулевых вспомогательных определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного из вспомогательных определителей).
В свете приведенных выше определений, теорема Крамера может быть сформулирована иначе: если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система является совместной определенной и при этом . (1.6)
Если главный определитель ∆=0, то система либо имеет бесконечное множество решений (при всех нулевых вспомогательных определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного из вспомогательных определителей).
В свете приведенных выше определений, теорема Крамера может быть сформулирована иначе: если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система является совместной определенной и при этом 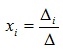 ; если главный определитель нулевой, то система является либо совместной неопределенной (при всех ∆i=0), либо несовместной (при отличии хотя бы одного из ∆i от нуля).
После этого следует провести проверку полученного решения.
Пример 1.4. Решить систему методом Крамера ; если главный определитель нулевой, то система является либо совместной неопределенной (при всех ∆i=0), либо несовместной (при отличии хотя бы одного из ∆i от нуля).
После этого следует провести проверку полученного решения.
Пример 1.4. Решить систему методом Крамера
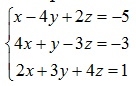 Решение. Так как главный определитель системы
Решение. Так как главный определитель системы
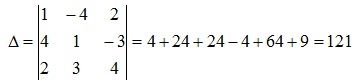 отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители
отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители
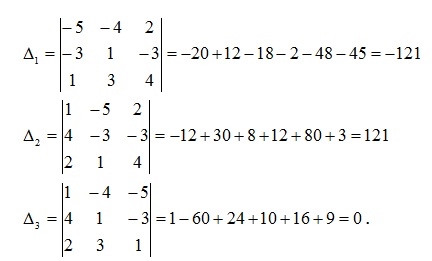 Воспользуемся формулами Крамера (1.6):
Воспользуемся формулами Крамера (1.6): 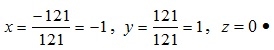 Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.
Таблица 1.4
Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.
Таблица 1.4
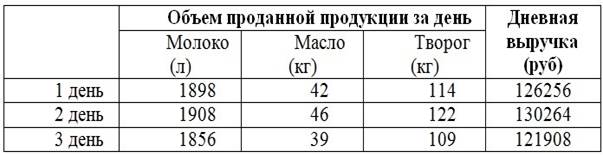 Определить стоимость 1 единицы продукции молокоцеха каждого вида.
Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z – 1 кг творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из трех дней реализации можно отобразить следующей системой:
Определить стоимость 1 единицы продукции молокоцеха каждого вида.
Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z – 1 кг творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из трех дней реализации можно отобразить следующей системой:
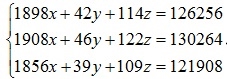 .
Решим систему методом Крамера. Найдем главный определитель системы по формуле (1.2): .
Решим систему методом Крамера. Найдем главный определитель системы по формуле (1.2):
 Так как он отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители с помощью формулы (1.2):
Так как он отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители с помощью формулы (1.2):
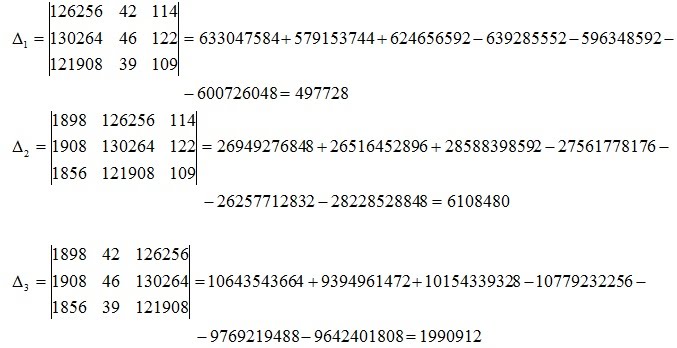 По формулам Крамера (1.6) имеем:
По формулам Крамера (1.6) имеем:
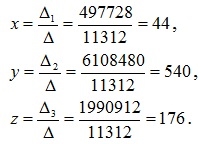 Вернувшись к обозначениям, видим, что стоимость 1 литра молока равна 44 рубля, 1 кг масла – 540 рублей, 1 кг творога – 176 рублей
Примечание. Как видно, процесс вычисления определителей вручную с помощью калькулятора трудоемок, поэтому на практике используют персональный компьютер. Так, для решения систем линейных алгебраических уравнений методом Крамера в MS Excel высчитывают ее главный и вспомогательные определители с использованием функции МОПРЕД(), где аргументом является диапазон ячеек и элементы матрицы, определитель которой находится.
Вернувшись к обозначениям, видим, что стоимость 1 литра молока равна 44 рубля, 1 кг масла – 540 рублей, 1 кг творога – 176 рублей
Примечание. Как видно, процесс вычисления определителей вручную с помощью калькулятора трудоемок, поэтому на практике используют персональный компьютер. Так, для решения систем линейных алгебраических уравнений методом Крамера в MS Excel высчитывают ее главный и вспомогательные определители с использованием функции МОПРЕД(), где аргументом является диапазон ячеек и элементы матрицы, определитель которой находится.
| 
|
Поиск по сайту:
|
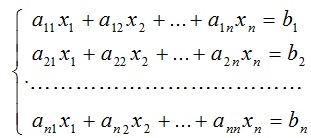 . (1.5)
Главной матрицей A системы линейных алгебраических уравнений называется матрица, составленная из коэффициентов, стоящих при неизвестных:
. (1.5)
Главной матрицей A системы линейных алгебраических уравнений называется матрица, составленная из коэффициентов, стоящих при неизвестных:
 .
Определитель главной матрицы системы называется главным определителем и обозначается ∆.
Вспомогательный определитель ∆i получается из главного определителя путем замены i-го столбца на столбец свободных членов
.
Определитель главной матрицы системы называется главным определителем и обозначается ∆.
Вспомогательный определитель ∆i получается из главного определителя путем замены i-го столбца на столбец свободных членов 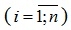 .
Теорема 1.1 (теорема Крамера). Если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, вычисляемое по формулам:
.
Теорема 1.1 (теорема Крамера). Если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, вычисляемое по формулам:
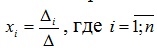 . (1.6)
Если главный определитель ∆=0, то система либо имеет бесконечное множество решений (при всех нулевых вспомогательных определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного из вспомогательных определителей).
В свете приведенных выше определений, теорема Крамера может быть сформулирована иначе: если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система является совместной определенной и при этом
. (1.6)
Если главный определитель ∆=0, то система либо имеет бесконечное множество решений (при всех нулевых вспомогательных определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного из вспомогательных определителей).
В свете приведенных выше определений, теорема Крамера может быть сформулирована иначе: если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система является совместной определенной и при этом 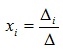 ; если главный определитель нулевой, то система является либо совместной неопределенной (при всех ∆i=0), либо несовместной (при отличии хотя бы одного из ∆i от нуля).
После этого следует провести проверку полученного решения.
Пример 1.4. Решить систему методом Крамера
; если главный определитель нулевой, то система является либо совместной неопределенной (при всех ∆i=0), либо несовместной (при отличии хотя бы одного из ∆i от нуля).
После этого следует провести проверку полученного решения.
Пример 1.4. Решить систему методом Крамера
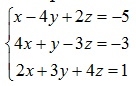 Решение. Так как главный определитель системы
Решение. Так как главный определитель системы
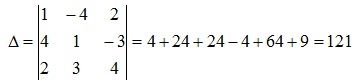 отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители
отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители
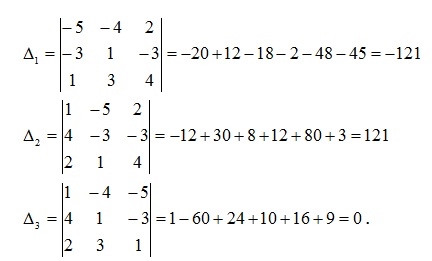 Воспользуемся формулами Крамера (1.6):
Воспользуемся формулами Крамера (1.6): 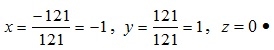 Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.
Таблица 1.4
Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.
Таблица 1.4
 Определить стоимость 1 единицы продукции молокоцеха каждого вида.
Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z – 1 кг творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из трех дней реализации можно отобразить следующей системой:
Определить стоимость 1 единицы продукции молокоцеха каждого вида.
Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z – 1 кг творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из трех дней реализации можно отобразить следующей системой:
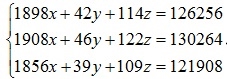 .
Решим систему методом Крамера. Найдем главный определитель системы по формуле (1.2):
.
Решим систему методом Крамера. Найдем главный определитель системы по формуле (1.2):
 Так как он отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители с помощью формулы (1.2):
Так как он отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители с помощью формулы (1.2):
 По формулам Крамера (1.6) имеем:
По формулам Крамера (1.6) имеем:
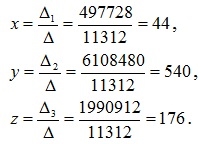 Вернувшись к обозначениям, видим, что стоимость 1 литра молока равна 44 рубля, 1 кг масла – 540 рублей, 1 кг творога – 176 рублей
Примечание. Как видно, процесс вычисления определителей вручную с помощью калькулятора трудоемок, поэтому на практике используют персональный компьютер. Так, для решения систем линейных алгебраических уравнений методом Крамера в MS Excel высчитывают ее главный и вспомогательные определители с использованием функции МОПРЕД(), где аргументом является диапазон ячеек и элементы матрицы, определитель которой находится.
Вернувшись к обозначениям, видим, что стоимость 1 литра молока равна 44 рубля, 1 кг масла – 540 рублей, 1 кг творога – 176 рублей
Примечание. Как видно, процесс вычисления определителей вручную с помощью калькулятора трудоемок, поэтому на практике используют персональный компьютер. Так, для решения систем линейных алгебраических уравнений методом Крамера в MS Excel высчитывают ее главный и вспомогательные определители с использованием функции МОПРЕД(), где аргументом является диапазон ячеек и элементы матрицы, определитель которой находится.
