Р а б о т а 8
Задание. Используя метод Лобачебского, решить уравнение с точностью до 0,001.
№1. x4+6x³+11x²-2x-28=0. № 2.x4+5x3+9x2+5x-1=0
№3. x4+3x+3x-2=0.№ 4.x4+x3-7x2+8x-6=0
№ 5. x4-10x3+16x+5=0 № 6.x4-3x3-4x2-x-3=0
№ 7. x4+4x3+4x2+4x-1=0 № 8.x4+6x3+13x2+10x+1=0
№ 9. x4+x3-4x2+16x-8=0 № 10.x4-x3-4x2-11x-3=0
№ 11. x4-6x2-12x-8=0 № 12.x4+4x3+4x2-4=0
№ 13. x4+x3+2x+1=0 № 14.x4+2x3+x2+2x+1=0
№ 15. x4+3x2-4x-1=0 № 16.x4+3x3+8x2-5=0
№ 17. x4-6x3+11x2+2x-28=0 № 18.x4-5x3+9x2-5x-1=0
№ 19. x4-3x3+3x2-2=0 № 20.x4-x3-7x2-8x-6=0
№ 21. x4-10x2-16x+5=0 № 22.x4+3x3+4x2+x-3=0
№ 23. x4-4x3-4x2-4x-1=0 № 24.x4+2x3+3x2+2x-2=0
№ 25. x4-6x3+13x2-10x+1=0 № 26.x4-3x2+4x-3=0
№ 27. x4-6x2+12x-8=0 № 28.x4-4x3+4x2-4=0
№ 29. x4-x3-2x+1=0 № 30.x4-2x3+x2-2x+1=0
| Образец выполнение задания x4-2x3+x-1,5=0 |
Вычисления помещаем в таблице:
| m | 2m | a0 | a1 | a2 | a3 | a4 |
| -2 | -1,5 | |||||
| 2,25 | ||||||
| -2,5 | -3,5 | 5,0625 | ||||
1,96·102
0,05·10
 2,01·102 2,01·102
| 6,25 10,125 114,375 | 12,25 25,3125 37,5625 | 25,629 | |||
| 2,01·10² | 1,1438·10² | 3,7562·10 | 2,5629·10 | |||
| 4,0401·104 -0,0229·104 4,0172·104 | 1,30828·104 -1,50999·104 +0,00513·104 -0,19658·104 | 1,4109·10³ -5,86629·10³ -4,4520·10³ | 6,5685·10² | |||
| 4,0172·104 | -1,19658·103 | -4,4520·10³ | 6,5685·10² | |||
| 1,6138·109 | 3,8644·106 35,7691·107 0·107 | 1,98203·107 0,25825·10 | 4,3145·105 | |||
| 1,6138·109 | 3,6155·108 | 2,2403·107 | 4,3145·105 | |||
| 2,6044·1018 | 13,0718·1016 -7,2308·1016 0·1016 | 5,0189·1014 -3,1198·1014 | 1,8615·1011 | |||
| 2,6044·1018 | 5,8410·1016 | 1,8991·1014 | 1,8615·1011 | |||
| 6,7829·1036 | 3,4117·1033 -0,9892·1033 | 3,6066·1028 -2,1746·1028 | 3,4652·1022 | |||
| 6,7829·1036 | 2,4225·1033 | 1,4320·1028 | 3,4652·1022 | |||
| 4,6008·1073 | 5,8685·1066 -0,1943·1066 | 2,05062·1056 -1,67899·1056 | 1,2008·1045 | |||
| 4,6008·1073 | 5,6742·1066 | 3,7173·1055 | 1,2008·1045 | |||
| m | 2m | a0 | a1 | a2 | a3 | a4 |
| 2,1167·10147 | 3,2197·10133 -0,0003·10133 | 1,3818·10111 -13,6272·10111 | 1,4419·1090 | |||
| 2,1167·10147 | 3,2194·10133 | -1,2245·10112 | 1,4419·1090 | |||
| 4,4804·10294 | 1,0365·10267 | 1,4994·10224 -0,9284·10224 | 2,0791·10180 | |||
| 4,4804·10294 | 1,0365·10267 | -0,5710 ·10224 | 2,0791·10180 |
1. lg|1x|=  ∙lg2.1167∙10147=
∙lg2.1167∙10147=  ∙ 147.3257=0.2877.
∙ 147.3257=0.2877.
|1x|=1.939; x1=1.939.
2. lg|2x|=  ∙ lg
∙ lg  =
=  ∙(-14+0,5077-0.3257)=
∙(-14+0,5077-0.3257)=
 (-13.8180)= - 0.02699=1.97301.
(-13.8180)= - 0.02699=1.97301.
|2x|=0,9397; x2= -0,9397
3. 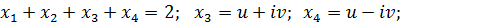
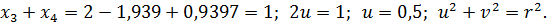



Ответ: 
Р а б о т а 9
Задание. Используя метод выделения квадратного множителя (метод Хичкока), решить уравнение с точностью до 0,001.
№ 1. 2x4+0,2x³+1,4x²+2,3x-1,5=0.№ 2. x4+0,77x³-1,002x²+60164x-1,6=0.
№ 3. x4+x³+2x+1=0. № 4. x4+1,4x³-2,26x²+0,5x-3,5=0.
№ 5. x4+2x³+x²+2x+1=0. № 6. x4+2,5x³-0,4x²+2,6x+7,2=0.
№ 7. x4+4x³+4x²+4x-1=0. № 8. x4+2x³-0,4x²+1,6x+0,64=0.
№ 9. x4+4x³+2,2x²+6,4x+2,56=0. № 10. x4-8x³-5x²-12x+2,25=0.
№ 11. x4+10x³+1,8x²-31x+9,61=0. № 12. x4-6x³-1,2x²-14,4x+5,76=0.
№ 13. x4+8x³-16x²+24,492x-1=0. № 14. x4-6x³-7x²-18x-1=0.
№ 15. x4-8x³-5x²-10x-1=0.№ 16. x4+6x³-5x²+24x+2=0.
№ 17. x4-8x³-10x²-40x+7=0.№ 18. x4+10x³-3x²+36x+2=0.
№ 19. x4+6x³-16x²+24x-2=0. № 20. x4-8x³-5x²-42x+6=0.
№ 21. x4-2x³+4,2x²-8x-1=0. № 22. x4+4x³+7,2x²+4x-1=0.
№ 23. x4-4x³+5,2x²-4=0. № 24. x4+2x³+6,2x²+10x+4=0.
№ 25. x4-2x³+4,2x²-8x-1=0.№ 26. x4-4x³+x²-10x-0,8=0.
№ 27. x4-4x³-19x²-26x+1=0. № 28. x4-4x³+4,2x²-10x-4=0.
№ 29. x4+4x³-19x²-10x+1=0. № 30. x4+4x³-2x²+14x+3,1=0.
| О б р а з е ц в ы п о л н е н и я з а д а н и я x4+4x³+4,8x²+16x-1=0. |
Определим какие-нибудь два корня уравнения; для этого определим знаки функции ƒ(х)=x4+4x³+4,8x²+16x-1=0 при некоторых значениях х;
| х | -4 | -3 | -2 | -1 | ||
| sign ƒ | + | - | - | - | - | + |
Итак, один корень принадлежит промежутку [0, 1], а другой - промежутку [-4, -3].
Примем х1≈ 0,5; х2 ≈ -3,5; тогда за начальное приближение квадратного трехчлена - делителя данного многочлена - можно взять
q0(x)=x²+(-0,5+3,5)x-3,5·0,5= x²+3x-1,75,
где р0=3, q0= -1,75.
Уточнение коэффициентов делителя производим по формулам
pk+1= pk+ hk; 
где


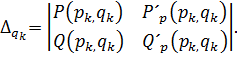
Значения производных находятся по формулам
P’p(pk, qk)= pkRk - Sk; P’q(pk, qk)= - Rk;
Q’k(pk, qk)= qkRk; Q’k(pk, qk)= - Sk;
Величины P(pk, qk) и Q(pk, qk) определяются из тоджества
ƒ(х)=qk(х)·Lk(x)+ Pk(pk, qk)·x+ Q’k(pk, qk),
а величины Rk и Sk из - тоджества
Lk(x)=qk(х)· L1k(x)+ Rk·x+Sk
Все расчеты можно оформить в виде двух вычислительных таблиц, одна из которых (табл. I) служит для двукратного деления на qk(х) по схеме Горнера, а другая (табл. II) - для вычисления поправокhkи tk.
Таблица I.
| k | 4,8 | -1 | ||||
| -p=-3 -q=1,75 -p=-3 -q=1,75 | -3 - -3 - -2= R0 | -3 1,75 3,55 - 1,75 5,30= S0 | -10,65 1,75 7,1= P0 | - 6,2125 5,2125= Q0 | ||
| -3,9 0,15 -3,9 0,15 | -3,9 - 0,1 -3,9 - -3,8= R1 | -0,39 0,15 4,56 - 0,15 4,71= S1 | -17,784 0,015 -1,769= P1 | - 0,684 -0,316= Q1 | ||
| -3,79 0,23 -3,79 0,23 | -3,79 - 0,21 -3,79 - -3,58= R2 | -0,7959 0,23 4,2341 - 0,23 4,4641= S2 | -16,0472 0,0483 0,0011= P2 | - 0,9738 -0,0262= Q2 | ||
| -3,7889 0,2361 -3,7889 0,2361 | -3,7889 - 0,2111-3,7889 - -3,5778 | -0,79984 0,2361 4,23626 - 0,2361 4,47236 | -16,05077 0,04984 -0,00093 | - 1,00018 0,00018 | ||
| -3,78885 0,2361 | -3,78885 - 0,21115 | -0,800016 0,23607 4,236054 | -16,04977 0,049846 -0,000076 | - 1,000005 0,000005 |
Таблица II.
| k | pk | Rk | Pk | P’p(pk, qk) | P’q(pk, qk) | ∆k | ∆pk | hk |
| qk | Sk | Qk | Q’k(pk, qk) | Q’k(pk, qk) | ∆qk | tk | ||
| -2 | 7,1 | -11,3 | 52,89 | 48,055 | 0,9 | |||
| -1,75 | 5,3 | 5,2125 | 3,5 | -5,3 | 83,751 | 1,6 | ||
| 3,9 | 3,8 | -1,769 | -19,53 | 3,8 | 89,82 | -9,533 | -0,11 | |
| -0,15 | 4,71 | -0, | 0,57 | -4,71 | -7,180 | -0,08 | ||
| 3,79 | -3,58 | 0,0011 | -18,0323 | 3,58 | 77,55 | -0,0889 | -0,0011 | |
| -0,23 | 4,4641 | -0,0262 | 0,8234 | -4,4641 | -0,4715 | -0,0061 | ||
| 3,7889 | -3,5778 | -0,0093 | -18,0283 | 3,5778 | 77,607 | -0,00352 | -0,00005 | |
| -0,2361 | 4,47236 | 0,00018 | 0,8447 | -4,47236 | 0,00246 | 0,00003 | ||
| 3,78885 | ||||||||
| -0,23607 |
Итак,
ƒ(х)≈(x²+3,78885х-0,23607)(x²+0,21115х+4,23605)=0.
Для определения корней остается решить два квадратных уравнения:
x²+3,78885х-0,23607=0; х1,2=-1,894425±  +0,23607= = -1,894425±1,955739; х1≈-3,850; х2≈0,0613;
+0,23607= = -1,894425±1,955739; х1≈-3,850; х2≈0,0613;
x²+0,21115х+4,23605=0; х3,4=-0,105575±  -4,23605=
-4,23605=
= -0,105575+2,055i; х3,4≈ -0,106+2,055i.
Ответ: х1≈-3,850; х2≈0,0613; х3,4≈ -0,106+2,055i.
Глава VI
НАХОЖДЕНИЕ СОБСТВЕННЫХ ЧИСЕЛ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦ
Задание. Найти собственные числа и собственные векторы матрицы методом непосредственного развертывания с точностью до 0,001.
№ 1.  № 2.
№ 2. 
№ 3.  № 4.
№ 4. 
№ 5.  № 6.
№ 6. 
№ 7.  . № 8.
. № 8. 
№ 9.  № 10.
№ 10. 
№ 11.  № 12.
№ 12. 
№ 13.  № 14.
№ 14. 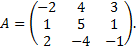
№ 15.  № 16.
№ 16. 
№ 17. 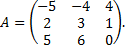 № 18.
№ 18. 
№ 19.  № 20.
№ 20. 
№ 21.  № 22.
№ 22. 
№ 23.  № 24.
№ 24. 
№ 25.  № 26.
№ 26. 
№ 27.  № 28.
№ 28. 
№ 29.  № 30.
№ 30. 
| О б р а з е ц в ы п о л н е н и я з а д а н и я |
1. Составим характеристические уравнение матрицы, корнями которого являются собственные числа матрицы.

Непосредственного развернув определить третьего порядка, получим
(2-λ)(4-λ)(-1-λ)-15-12-9(4-λ)-10(2-λ)-2(-1-λ)=0,
Откуда после раскрытия скобок, приведения подобных членов и умножения обеих частей уравнения на - 1 имеем
λ³-5λ²-19λ+89=0.
Полученное уравнение решим с помощью метода Ньютона для уточнения корней, предварительно отделив корни. Находим
ƒ(λ)=λ³-5λ²-19λ+89; ƒ(λ)=3λ²-10λ-19;
 λ1= -1,2; λ2=4,7.
λ1= -1,2; λ2=4,7.
Составим таблицу знаков фуекции ƒ(λ):
| λ | -∞ | -1,2 | 4,7 | +∞ |
| sign ƒ(λ) | - | + | - | + |
Из таблицы знаков видим, что уравнение имееи три действительных корня λ1ϵ ]-∞; -1,2]; λ2ϵ [ -1,2; 4,7]; λ3ϵ [ 4,7; +∞ [. Выберем для уточнения один из них, например λ2.
Уменьшим промежуток [-1,2; 4,7], в которм находится этот корень. Для этого вычислим значения функции ƒ(λ) в некоторых точках промежутка: ƒ(2)=39>0; ƒ(3)=14>0; ƒ(4)=-3<0. Итак, корень λ2содержится внутри промежутка [3, 4].
Уточнения корня производим по формуле

Для выбора начального приближения λ0 определим знак второй производной ƒ″(λ)в промежутке [3, 4]; имеем ƒ″(λ)=6λ-10; ƒ″(λ)>0 при 3≤ λ ≤4; значит, λ0=3.
Для вычисления значений функций и ее производной будем использовать схему Горнера. Корень определим с четырьмя верными десятичьными знаками.
Все вычисления распологаем в трех таблицах. В табл. 1 вычисляем значения функции ƒ(λ), в табл. II - значения производной ƒꞌ(λ), а в табл. III производим уточнение λ.
Таблица I.
| n | λ n | -5 | -10 | ||
| -6 | -75 | ||||
| -2 | -25 | ||||
| 3,63 | 3,63 | 4,9731 | -87,0224 | ||
| -1,37 | -239731 | -1,9776 | |||
| 3,75 | 3,75 | -4,6875 | -88,8281 | ||
| -1,25 | -23,6875 | 0,1719 | |||
| 3,762 | 3,762 | -4,6574 | -88,9991 | ||
| -1,238 | -23,6574 | 0,0009 | |||
| 3,7621 | 3,7621 | -4,65710 | -89,0004 | ||
| -1,2379 | -2365710 | -0,0004 |
Таблица II.
| n | λ n | -10 | -19 | |
| -3 | ||||
| -1 | -22 | |||
| 3,63 | 10,89 | 3,2307 | ||
| 0,89 | -15,7693 | |||
| 3,75 | 11,25 | 4,6875 | ||
| 1,25 | -14,3125 | |||
| 3,762 | 11,286 | 4,8379 | ||
| 1,286 | -14,1621 |
Таблица III.
| n | λ n | ƒ(λn) | ƒꞌ(λn) | ƒꞌ(λn)/ ƒꞌ(λn) |
| -22 | -0,63 | |||
| 3,63 | 1,9776 | -15,7693 | -0,12 | |
| 3,75 | 0,1719 | -14,3125 | -0,012 | |
| 3,762 | 0,0009 | -14,1621 | -0,00006 | |
| 3,7621 |
Итак, λ2 ≈3,7621.
Для определения двух других собственных чисел решим квадратное уравнение, полученное при делении многочлена ƒ(λ) на λ - 3,7621:


2. Для определения собственных векторов, соответствующих найденным числам, воспользуемся системами линейных уравнений, полученными из равенства (А - λЕ)Х=0.
При λ1= -4,2841 получим систему

Эта система линейних однородных уравнений является неопределенной, так как ее главный определитель равен нулю.
Решение можно найти, используя любые два уравнения системы, например второе и третье:

Или
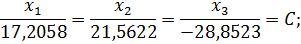
Для того чтобы норма ‖ Х1‖вектора была равна единице, разделим все его координаты на наибольшую из них по абсолютной величине; тогда получим Х1=С(-0,597; -0,746; 1).
При λ2 = 3,7621 имеем



При 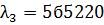 имеем:
имеем:



Ответ:

| 
| 
| 
|
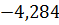 3,762
5,522
3,762
5,522
| 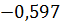


| 


| 


|
Работа2
Задание. Используя метод Крылова, найти собственные числа и собственные векторы матрицы. Собственные числа определить с четырьмя верными цифрами, а собственные векторы – с тремя десятичными знаками.
№ 1. 