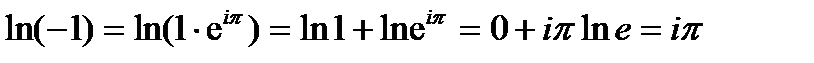Комплексным числом называется число вида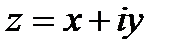 
, где 
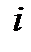- мнимая единица, по определению 
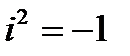, а 
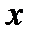и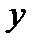 
обычные действительные числа. Число 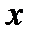называется действительной частью комплексного числа, пишется 
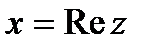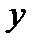, а - мнимая часть, пишется 
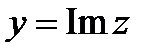. Каждое комплексное число можно рассматривать как упорядоченную пару чисел 
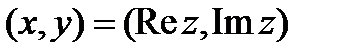, вектор или точку на комплексной плоскости. Комплексная плоскость вводится следующим образом. Строятся две ортогональные оси, по горизонтальной оси откладывается 
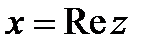, а по вертикальной 
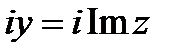(рис. 8.1).
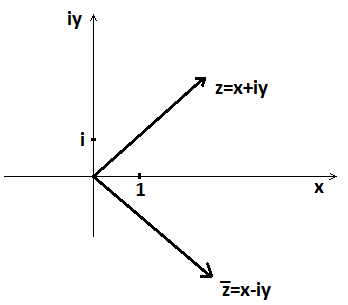
Рис. 8.1 Комплексное число как вектор на комплексной плоскости.
Комплексное число вида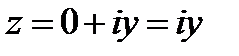 
называется мнимым числом. Комплексное число 
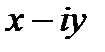называется комплексно сопряженным к 
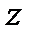и обозначается 
.
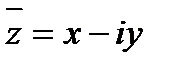Введение комплексных чисел позволяет сформулировать Великую теорему алгебры. Всякий полином (многочлен) степени n имеет ровно n корней. Например, уравнение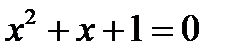 
с отрицательным дискриминантом 
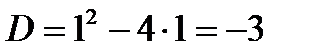имеет два корня
, 
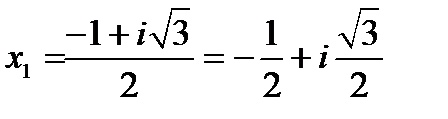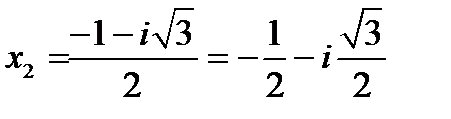
Комплексные корни квадратного уравнения всегда являются комплексно сопряженными числами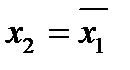 
.
Для комплексных чисел вводятся арифметические операции по следующим правилам.
1. При сложении комплексных чисел отдельно складываются их действительные и мнимые части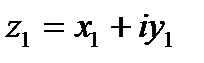 
, 
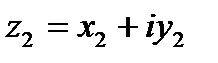. Тогда
.
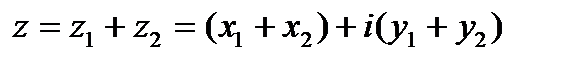Для комплексно сопряженных чисел
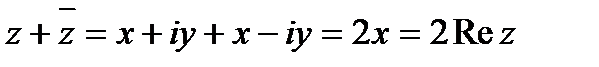
Отсюда
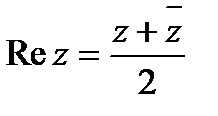
2. При вычитании двух комплексных чисел отдельно вычитаются их действительные и мнимые части
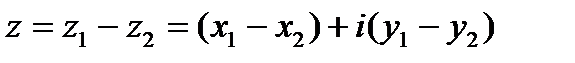
Для комплексно сопряженных чисел
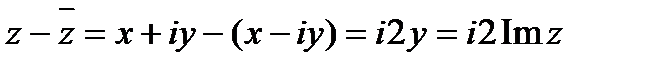
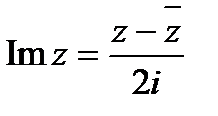
3. Произведением комплексных чисел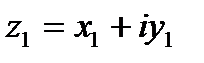 
и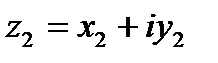 
называется комплексное число:
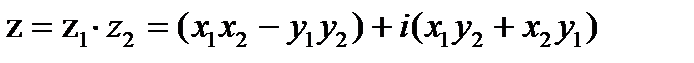
Это выражение легко получить, раскрыв скобки в произведении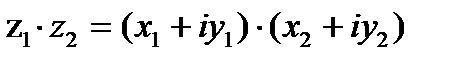 
и учтя, что i 2 = – 1.
Произведение двух сопряжённых комплексных чисел равно действительному положительному числу.
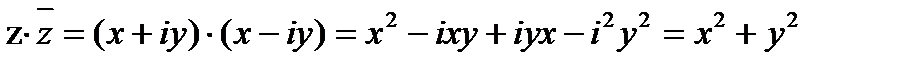
(Сравним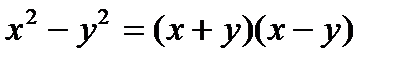 
).
4. Разделить комплексное число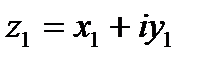 
на другое 
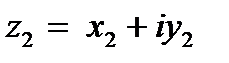- значит найти третье число 
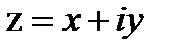, которое будучи умноженным на делитель 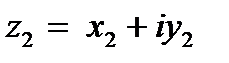даёт в результате делимое 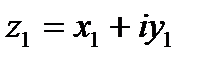, т.е. 
.
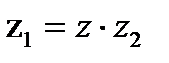Для того чтобы получить результат, надо и числитель, и знаменатель умножить на число, сопряженное к знаменателю и довести преобразования до вида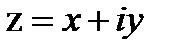 
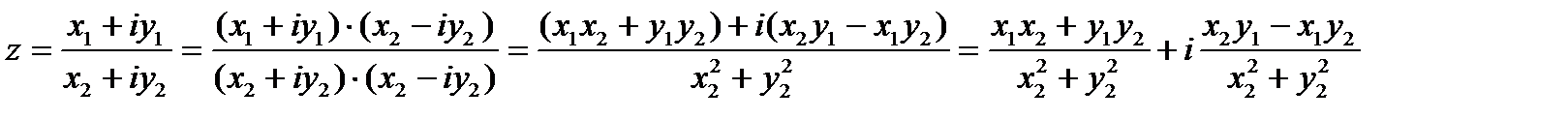
Например. Проведем все введенные арифметические операции для пары комплексных чисел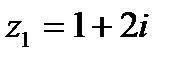 
, 
.
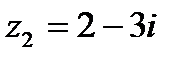1. Комплексное сопряжение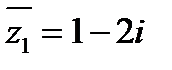 
, 
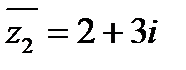
2. Сложение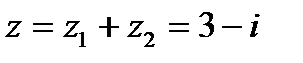 
3. Вычитание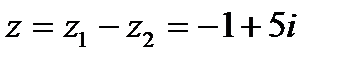 
4. Умножение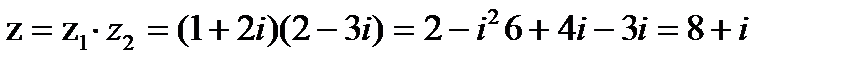 
5. Деление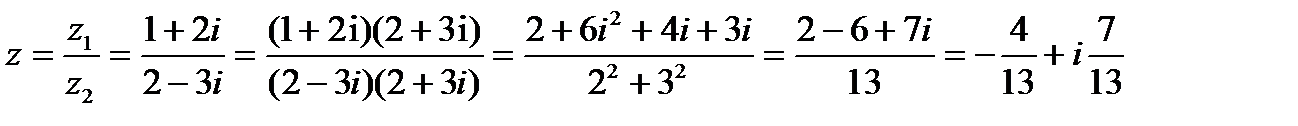 
Введение операции умножения позволяет возводить комплексные числа в степень
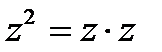
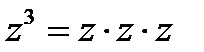
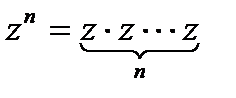
и извлекать корень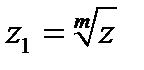 
, если 
.
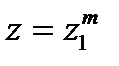Например,
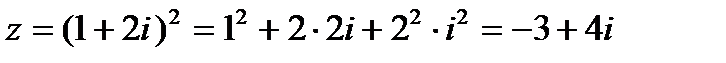
Комплексные числа имеют разные формы записи. Форма 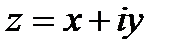называется декартовой.
Если ввести на комплексной плоскости полярную систему координат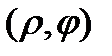 
, то связь между координатами будет задаваться следующими соотношениями
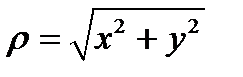
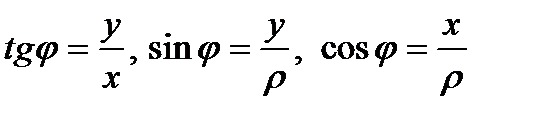
Так как тангенс π периодическая функция, то при нахождении φ необходимо учитывать знаки синуса и косинуса или делать чертеж, определяя в какой четвери находится комплексное число. Здесь число ρ называется модулем комплексного числа и имеет другое обозначение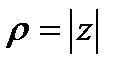 
, а φ - аргумент комплексного числа.
Обратные соотношения
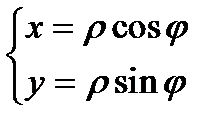
Подставив выражения для х и у вдекартову форму, получим тригонометрическую форму комплексного числа
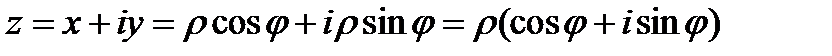
Переход в тригонометрическую форму позволяет существенно упростить операции умножения, деления, возведение в степень и извлечения корня из комплексных чисел Операции с комплексными числами, представленными в тригонометрической форме.
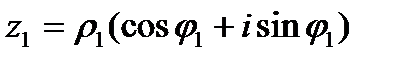
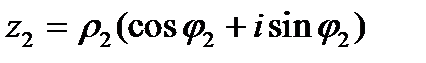
1. Умножение
.
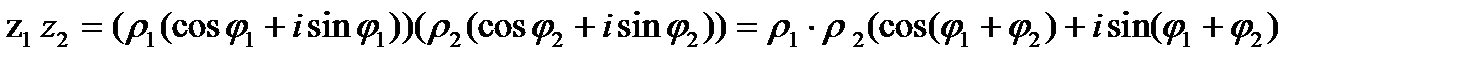Формулу легко получить, перемножив комплексные числа, 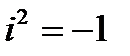, и учтя формулу тригонометрии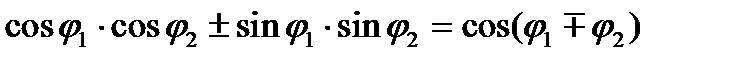 
2. Деление
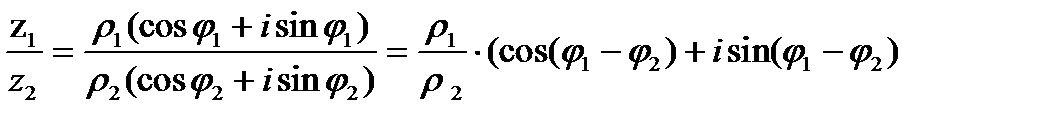
Действительно
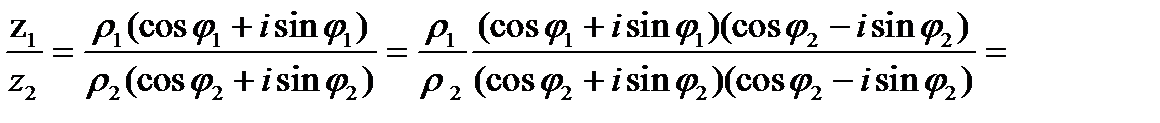
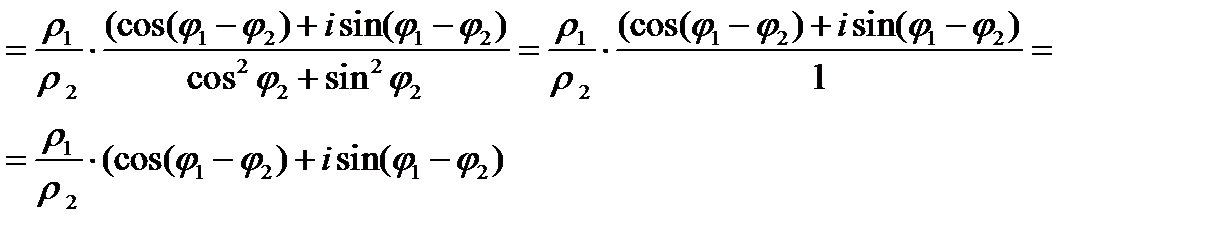
3. Возведение в степень
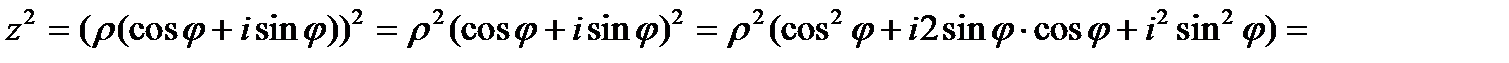
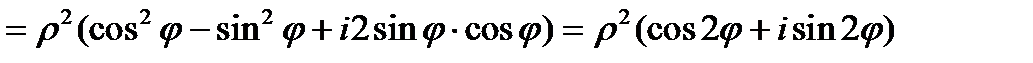
Здесь учено, что по формулам тригонометри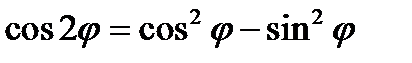и 
и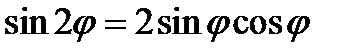 
По методу математической индукции можно доказать, что
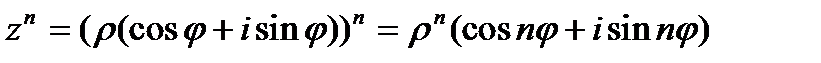
Эта формула называется первой формулой Муавра
Т.е. при возведении в степень числа в комплексной форме его модуль возводится в степень n, а аргумент умножается на n.
4. Извлечение корня. Извлечение корня проводится по второй формуле Муавра
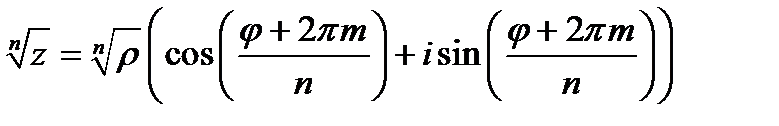
где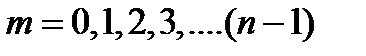 
.
Так как m принимает ровно n значений, то имеется ровно n корней.
Пример 1. Найдем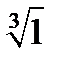 
. Так как корень третьей степени, о должно быть ровно три ответа. Переведем 1 в тригонометрическую форму 
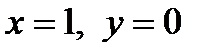, следовательно
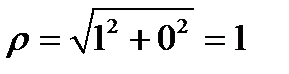
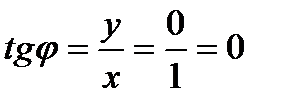
Есть два угла с таким тангенсом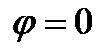 
и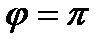 
. Строим чертеж (рис. 8.2)
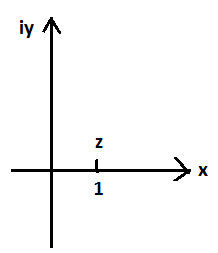
Рис. 8.2. Комплексное число z = 1+ 0 i
По чертежу выбираем 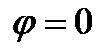. Следовательно, 
.
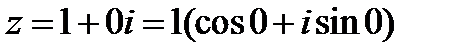Извлекаем корень третьей степени
, 
.
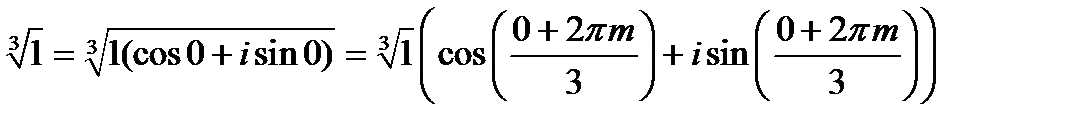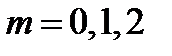Подставим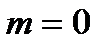 
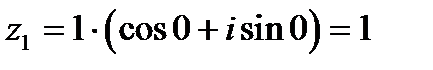
Подставим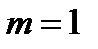 
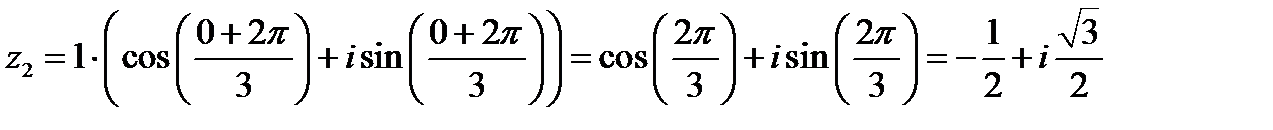
Подставим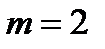 
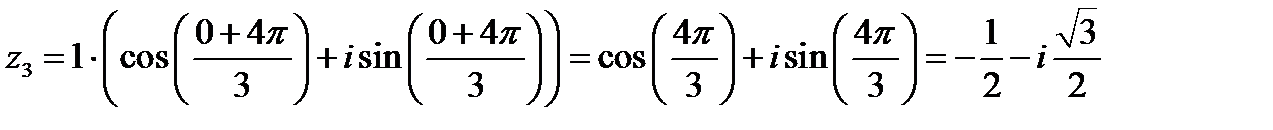
Пример 2. Вычислим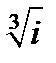 
. Повторяем все действия по той же схеме. 
, 
, 
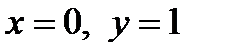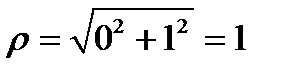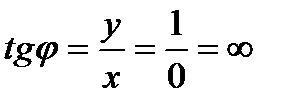. Есть два угла с таким тангенсом 
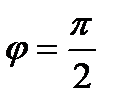и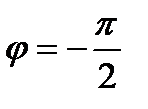 
.
По чертежу 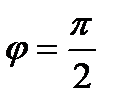(рис. 8.3)
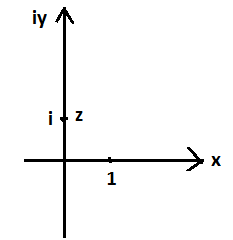
Рис. 8.3. Комплексное число z = 0 + 1 i
Следовательно
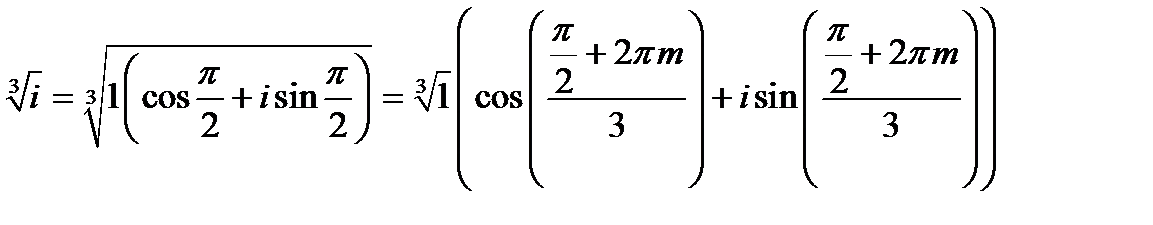
Подставим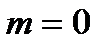
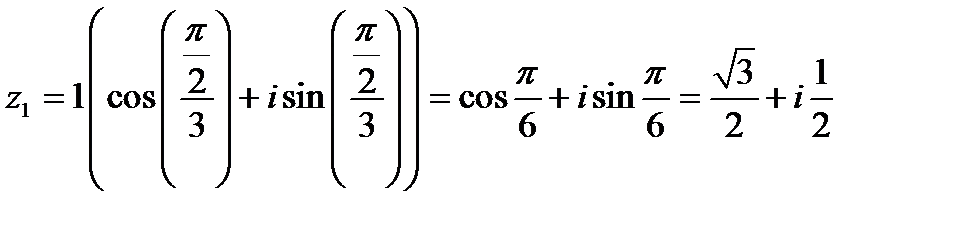
Подставим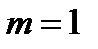
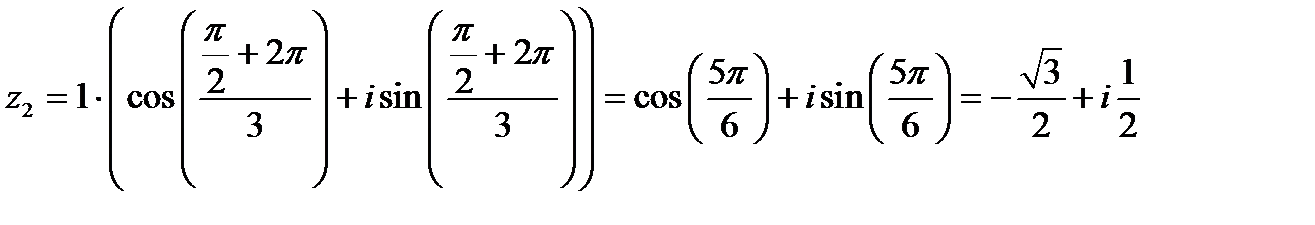
Подставим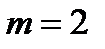
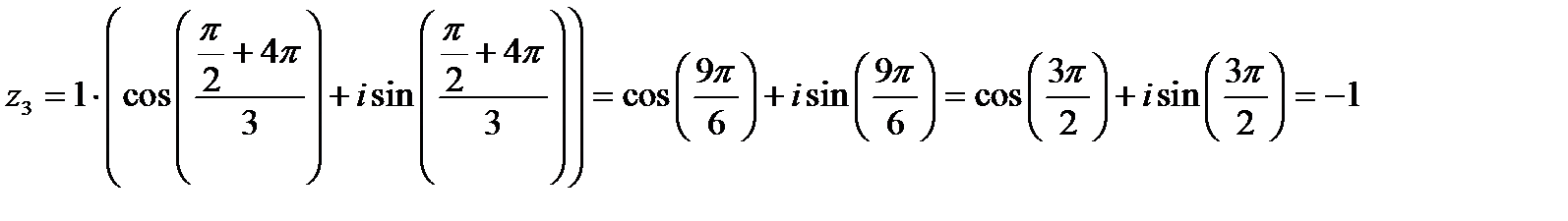Формулы Эйлера.
Формулы Эйлера связываю между собой тригонометрические функции и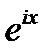 
, т. е. число е в степени ix.
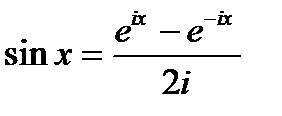
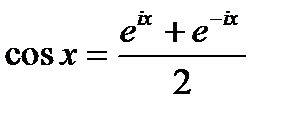
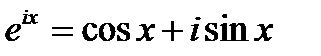
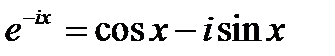
Эти формулы позволяют ввести эйлерову форму комплексного числа
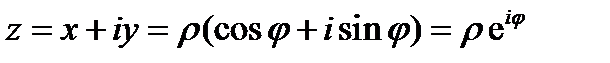
Так как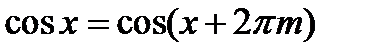 
и 
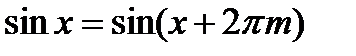, то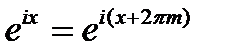 
, то есть является периодической функцией. Натуральный логарифм от комплексного числа обозначается 
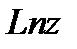и он равен 
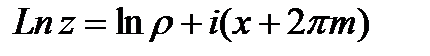, где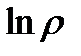 
обычный логарифм вещественного числа.
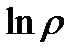называется действительной частью логарифма и определяется однозначно, а мнимая часть имеет бесконечное множество значений, отличающихся на 2π. Значение логарифма, мнимая часть которого находится в интервале 
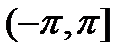называется главным значением логарифма и обозначается 
.
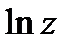Например,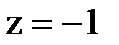 
. Найдем главное значение логарифма 
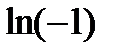. Переведем логарифм в эйлерову форму.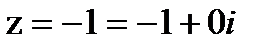 
, 
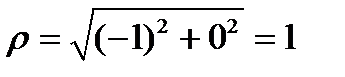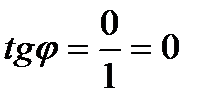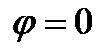, и .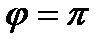
По чертежу выбираем 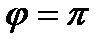(рис. 8. 4)
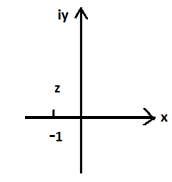
Рис. 8.4. Комплексное число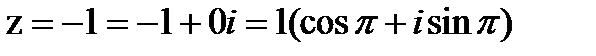 
.
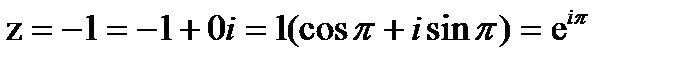Тогда 