Стековая организация рекурсии.

РЕКУРСИЯ

«Итерация свойственна людям, рекурсия - богам...»

Процедура или функция может обращаться к самой себе. Такой вызов называется рекурсией(от латинского recursio – возвращение).

· Алгоритм называется рекурсивным, если в его определении содержится прямой или косвенный вызов этого же алгоритма.

Основной метод построения рекурсивных алгоритмов – это метод декомпозиции.

· Идея метода состоит в разделении задачи на части меньшей размерности, получение решения для полученных частей и объединение решений.

Рассмотрим функцию факториала n!. Как правило, ее определяют как произведение первых n чисел:

n! = 1∙2∙3…∙n.

Такое произведение легко вычислить с помощью итеративных конструкций, например:

f:= 1;

For i:= 1 To n Do f:= f * i;

 

С другой стороны ее можно определить рекурсивно следующим образом:

 

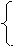0! = 1,

n! = n (n-1) !, если n>0,

или в виде функции:

 

F (0) = 1, (1)

F (n) = n · F (n -1), если n >0. (2) рекуррентное соотношение

 

· (2) – рекуррентные соотношение выражает значение функции при помощи других значений, вычисленных для меньших аргументов.

· (1) – нерекурсивно определенное начальное значение функции. Для каждой рекурсивной функции нужно хотя бы одно начальное значение, в противном случае ее нельзя вычислить в явном виде.

 

Function F (i:Integer): LongInt; {вычисление факториала}

Begin

If i = 1 Then F:= 1

Else F:= i*F (i – 1);

End;

Вызов: ….. Ввод n; WriteLn(‘ n!= ‘, Fact(n)); …….

 

Аналогично числа Фибоначчи определяются следующей последовательностью целых чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,… Эти числа можно получить исходя из рекуррентного соотношения:

 

F (n) = F (n - 1) + F (n - 2),F (0) = 0, F (1) = 1.

 

Определенные здесь числа Фибоначчи являются решением следующей задачи: Каждый месяц самка из пары кроликов приносит двух кроликов (самца и самку). Через два месяца новая самка сама приносит пару кроликов. Нужно найти число кроликов в конце года, если в начале года была одна новорожденная пора кроликов и в течение этого года кролики не умирали. (Задача сформулирована в 1202 г. итальянским математиком Фибоначчи (Леонардо Пизанский)).

Если для факториала первое (итеративное) определение может показаться проще, то для чисел Фибоначчи рекурсивное определение выглядит для вычислений лучше, чем прямая формула:

 

;

 

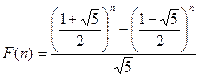Function F(i:Integer): Integer; {вычисление чисел Фибоначчи}

Begin

Case i Of

0..1: F:= i;

Else F:= F (i – 1) + F (i – 2);

End;

End;

Вызов: ….. Ввод n; WriteLn(‘ n!= ‘, F(n)); …….

 

Организовать вычисления по рекуррентным формулам можно и без использования рекурсии. Однако при этом встает вопрос о качестве программы и доказательстве ее эквивалентности начальным формулам. Использование рекурсии позволяет легко (почти дословно) запрограммировать вычисления по рекуррентным формулам.

Рекурсию можно рассматривать как процесс последовательного разложения (декомпозицию) задачи на серию подзадач двух типов: тех, которые мы решать умеем и тех, которые в чем-то аналогичны исходной задаче. В последнем случае каждая из полученных подзадач должна быть упрощенным вариантом предыдущей задачи.

Программы, в которых используются рекурсивныепроцедуры отличаются простотой, наглядностью и компактностью текста. Однако за простоту приходится расплачиваться неэкономным использованием оперативной памяти, так как выполнение рекурсивных процедур требует значительно большего размера оперативной памяти во время выполнения, чем нерекурсивных. Поясним сказанное более подробно.

Стековая организация рекурсии.

Для создания рекурсивных программ необходимо и достаточно наличие понятия процедуры и функции. Это вытекает из того, что процедуры и функции позволяют дать любой последовательности (операторов) имя, с помощью которого можно будет эту последовательность действий вызывать.

Как правило, с процедурой связывают множество локальных объектов, т.е. множество переменных, констант, типов и процедур, которые определены только в этой процедуре и вне ее не существуют или не имеют смысла.

Стек контекстов
..................	........
..................	i+1-й контекст
Состояние РОН	i-й контекст
Локальные переменные процедуры
Адрес возврата
Параметры процедуры
..................	i-1-й контекст
................	........

При каждой рекурсивной активации такой процедуры порождается новое множество локальных связанных переменных в специальной области памяти, называемой стеком. Хотя они имеют те же самые имена, что и соответствующие элементы локального множества предыдущего «поколения» этой процедуры, их значения отличны от последних, любые конфликты по именам разрешаются по правилу: идентификатор всегда относится к самому последнему порожденному множеству переменных. Поэтому, воспользоваться значением переменной a i -го уровня рекурсии можно находясь только на этом i -м уровне. Это же правило справедливо и для параметров процедуры. Например, если процедура Р имеет параметр а и вызывает саму себя, то параметр а этой вновь вызванной процедуры будет являться совершенно другим параметром; при возвращении в первую процедуру Р значение первого параметра а будет сохранено.

Итак, в момент вызова процедуры в памяти создается ее контекст: выделяется место под все ее параметры, локальные переменные и константы. Уничтожается этот контекст только после того, как будет достигнут оператор End, закрывающий процедуру, либо в ее тексте встретится оператор Exit, насильственно прерывающий ее выполнение. Таким образом на внутреннем уровне организован стек контекстов подпрограмм.

Замечание. Не следует понимать буквально, что при каждом рекурсивном вызове в памяти создается полная копия процедуры – запоминаются только текущие значения ее локальных объектов и параметров, сам код процедуры, конечно, в памяти существует в единственном экземпляре.Понятием полной копии рекурсивной процедуры пользуются лишь для упрощения анализа механизма рекурсии и облегчения первоначального его восприятия.

 

Пример. Вычислить сумму элементов в массиве а [1..n] целых чисел.

Function Sum (i:Integer): Integer;

Begin

If i>n Then Sum:=0

Else Sum:=a[i] + Sum (i + 1);

End;

Как видно из рис.2.1 вначале рекурсивные вызовы порождают «копии» процедуры (точнее функции), в каждой из которой активизируется незавершенная операция сложения a [ i ] +... При достижении уровня n +1 начинается возврат и накопление суммы, начиная с последнего элемента массива. Завершается процесс возвратом в головную программу с окончательным результатом. Подобно операторам цикла, рекурсивные процедуры могут приводить к не заканчивающимся вычислениям, и поэтому на эту проблему следует особо обратить внимание.

Очевидно, для того чтобы работа когда-либо завершилась, необходимо, чтобы рекурсивное обращение к Р управлялось некоторым условием В, которое в какой-то момент перестанет выполняться. Если не ограничивать число рекурсивных вызовов, может быстро возникнуть переполнение стека, особенно если у процедур много параметров и локальных переменных. Поэтому следует избегать рекурсии там, где существует очевидное итеративное решение, как например, при вычислении факториала.

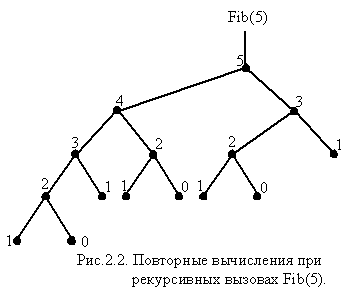· Итеративное решение может оказаться предпочтительным не только по расходу памяти, но и по объему вычислительных затрат. Продемонстрируем это утверждение на примере вычисления чисел Фибоначчи. Вычисление n -го элемента с помощью описанной функции Fib (n) приводит к ее рекурсивным активациям. Как часто это происходит? Каждое обращение с n>1 приводит к двум обращениям, т.е. общее число вызовов растет экспоненциально (рис.2.2).

Ясно, что такая программа практиче­ского интереса не представ­ляет. Однако, числа Фибоначчи можно вычислять и по итеративной схеме, где с помощью вспомогательных перемен­ных

x = F (i)и y = F (i – 1) удается избежать повторных вычислений од­ной и той же величины:

……………………..

i:=1;

a:=1;

b:=0;

While i < n Do

Begin

F:= a;

a:= a+b;

b:= F;

Inc(i);

End;

Write(F);

……………………..

Замечание. Рассмотренные примеры показывают, что применение рекурсивных определений само по себе не приводит к хорошим решениям задач. Так, задачи вычисления факториала и чисел Фибоначчи допускают более эффективные и достаточно простые итеративные решения. В примерах видно, что рекурсия в них моделирует простой цикл, тратя время на вычисления, связанные с управлением рекурсивными вызовами и память на динамическое хранение данных.

Итак, урок таков: следует избегать рекурсий там, где есть очевидное итерационное решение. Однако это не означает, что от рекурсий следует избавляться любой ценой. Существует много хороших примеров применения рекурсии, что мы и продемонстрируем в последующих разделах. То, что существуют реализации рекурсивных процедур на фактически нерекурсивных машинах, доказывает, что для практических целей любую рекурсивную программу можно трансформировать в чисто итеративную. Однако это требует явной работы со стеком для рекурсий, причем эти действия часто настолько затуманивают суть программы, что ее бывает трудно понять. Вывод: алгоритмы, рекурсивные по своей природе, а не итеративные, нужно формулировать как рекурсивные процедуры.

Определения.

Прямая рекурсия - непосредственный вызов алгоритма (функции, процедуры) F из текста самого алгоритма F.

Косвенная (взаимная) рекурсия - циклическая последовательность вызовов нескольких алгоритмов F₁, F₂, …, F_k (функций, процедур ) друг друга: F₁ вызывает F₂, F₂ вызывает F₃, …, F_k вызывает F₁ (k> 1).

Линейная рекурсия - тип рекурсии, при которой рекурсивные вызовы на любом рекурсивном срезе, инициируют не более одного последующего рекурсивного вызова.

Каскадная (древовидная) рекурсия - при каскадной рекурсии, рекурсивные обращения, как правило, приводят к необходимости многократно решать одни и те же подзадачи. И поэтому, по возможности, от неё или следует избавляться или предпринимать шаги, освобождающие от необходимости производить повторные решения подзадач.

Возвратная рекурсия - рекурсивная реализация метода перебора с возвратом (backtracking).

Рекурсивный стек - область памяти, в которую заносятся значения всех локальных переменных алгоритма (программы) в момент рекурсивного обращения. Каждое такое обращение формирует один слой данных стека. При завершении вычислений по конкретному обращению из стека считывается соответствующий ему слой данных, и локальные переменные восстанавливаются, снова принимая значения, которые они имели в момент обращения.

Глубина рекурсии – максимальное число рекурсивных вызовов процедуры без возвратов, которое происходит во время выполнения программы.

Текущий уровень рекурсии – число рекурсивных вызовов в каждый конкретный момент времени.

Рекурсивный спуск – движение вычислительного процесса в направлении последовательных рекурсивных вызовов.

Рекурсивный подъем – движение вычислительного процесса в направлении возврата из ранее вызванных копий рекурсивной процедуры.