Рассмотрим прямые  и
и  .
.
1. Прямые пересекаются, если
 . (4.9)
. (4.9)
Угол между прямыми находят по формуле:
 . (4.10)
. (4.10)
Например, прямые  и
и  пересекаются, так как
пересекаются, так как  , а
, а 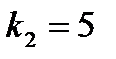 и
и  . Найдем угол между этими прямыми. Так как
. Найдем угол между этими прямыми. Так как  , то
, то  .
.
2. Прямые перпендикулярны, если выполняется условие:
 (4.11)
(4.11)
3. Прямые параллельны, если
 и
и  . (4.12)
. (4.12)
Например, прямые  и
и  параллельны, так как
параллельны, так как  и
и  .
.
4. Прямые совпадают, если:
 и
и 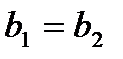 . (4.13)
. (4.13)
Пример 4. Запишите уравнение прямой, если известно, что эта прямая проходит через точку  и перпендикулярна прямой
и перпендикулярна прямой  .
.
Решение. Запишем уравнение данной прямой в виде 4.3:
 ,
,  .
.
Так как искомая прямая  перпендикулярна данной прямой, то выполняется равенство 4.11:
перпендикулярна данной прямой, то выполняется равенство 4.11:  , откуда
, откуда  .
.
Согласно формуле 4.4 запишем:
 или
или  .
.
Ответ: 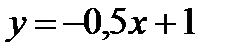 .
.
Расстояние от точки  до прямой
до прямой 
находят по формуле:
 . (4. 14)
. (4. 14)
Пример 5. Найдите длину высоты АD треугольника АВС, если  ,
,  ,
,  .
.
Решение. 1. Согласно формуле 4.6 запишем уравнение стороны ВС этого треугольника:  , откуда
, откуда  ,
,  ,
,  ,
,  .
.
2. Так как  , то длину отрезка AD найдем по формуле 4.14:
, то длину отрезка AD найдем по формуле 4.14:  .
.
Ответ: 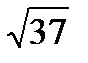 .
.
Кривые второго порядка
Уравнение линии второго порядка:
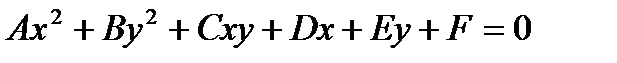 (4.15)
(4.15)
Рассмотрим некоторые виды линий второго порядка.
1. Окружность – это геометрическое место точек, равноудаленных от данной точки, называемой центром.
В случае окружности уравнение 4.15 примет вид:
 .
.
Рассмотрим расположение окружности на координатной плоскости.
Если центр окружности находится в точке  , а ее радиус равен R (рис. 4.4), то уравнение окружности имеет вид:
, а ее радиус равен R (рис. 4.4), то уравнение окружности имеет вид:
 . (4.16)
. (4.16)
Если центр окружности находится в точке  , а ее радиус равен R (рис. 4.5), то уравнение окружности имеет вид:
, а ее радиус равен R (рис. 4.5), то уравнение окружности имеет вид:
 . (4.17)
. (4.17)
| y |
| х |
| y |
| O |
| R |
| x |
| O |
| О/ |
| а |
| b |
Рис. 4.4 Рис. 4.5
Например, запишем уравнение окружности с центром в точке  и радиусом
и радиусом  . Получим:
. Получим:  .
.
Пример 6. Найдите сумму координат центра окружности  .
.
Решение. В данном уравнении выделим полные квадраты:
 ,
,  ,
, 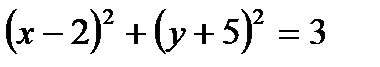 .
.
Получили окружность с центром в точке  и радиусом
и радиусом  .
.
Ответ: – 3.
2. Эллипс – это геометрическое место точек, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная. Расстояние от точки до фокуса называют фокальным радиусом.
Каноническое уравнение эллипса:
 , (4.18)
, (4.18)
где a – большая полуось; b – меньшая полуось.
Фокусы имеют координаты  и
и 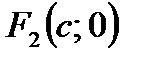 , где
, где
 . (4.19)
. (4.19)
На рисунке 4.6: 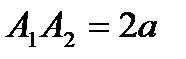 – большая ось эллипса;
– большая ось эллипса;  – малая ось эллипса;
– малая ось эллипса;  – расстояние между фокусами.
– расстояние между фокусами.
| В 1 |
| В 2 |
| А 1 |
| А 2 |
| F |
| b |
| y |
| -a |
| - b |
| O |
| x |
| a |
| O |
| F 2 |
| F 1 |
Рис. 4.6
Эксцентриситет эллипса находят по формуле:
 . (4.20)
. (4.20)
Если же  , то
, то  , а
, а  .
.
Пример 7. Составьте каноническое уравнение эллипса, если его большая ось равна 10, а эксцентриситет равен 0,4.
Решение. Так как  , то
, то  . Так как
. Так как  и
и  , то
, то  . Зная, что
. Зная, что  , запишем
, запишем  , откуда
, откуда  .
.
Каноническое уравнение эллипса: 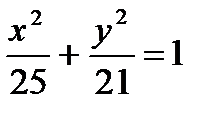 .
.
Ответ:  .
.
3. Гипербола – это геометрическое место точек, для каждой из которых модуль разностей расстояний до двух данных точек, называемых фокусами, есть величина постоянная.
Каноническое уравнение гиперболы:
 , (4.21)
, (4.21)
где a – действительная полуось; b – мнимая полуось.
Фокусы имеют координаты  и
и 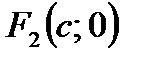 , где
, где
 . (4.22)
. (4.22)
На рисунке 4.7: 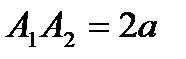 – действительная ось гиперболы;
– действительная ось гиперболы;  – мнимая ось;
– мнимая ось;  – расстояние между фокусами; точки А 1 и А 2 – ее вершины.
– расстояние между фокусами; точки А 1 и А 2 – ее вершины.
| В 2 |
| А 1 |
| F 1 |
| х |
| y |
| O |
| F 2 |
| В 1 |
| А 2 |
Рис. 4.7
Эксцентриситет гиперболы находят по формуле:
 . (4.23)
. (4.23)
Уравнения асимптот гиперболы:
 . (4.24)
. (4.24)
Пример 8. Запишите уравнение гиперболы и найдите расстояние между фокусами, если действительная ось гиперболы равна 10, а ее мнимая полуось равна 2.
Решение. Так как 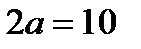 , то
, то  . По условию задачи
. По условию задачи  .
.
Запишем каноническое уравнение гиперболы:  .
.
По формуле 4.22 найдем с:  .
.
Найдем расстояние между фокусами:  .
.
Ответ:  ;
;  .
.
4. Парабола – это геометрическое место точек, равноудаленных от фокуса и прямой, называемой директрисой.
Каноническое уравнение параболы:
 (4.25)
(4.25)
где ось OX – ось симметрии параболы; p – расстояние от фокуса до директрисы (рис. 4.8).
Фокус имеет координаты  . Уравнение директрисы параболы имеет вид
. Уравнение директрисы параболы имеет вид 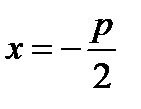 .
.
Если осью симметрии параболы является ось OУ, то каноническое уравнение параболы имеет вид:
 (4.26)
(4.26)
В этом случае фокус имеет координаты  , а уравнение директрисы d параболы имеет вид
, а уравнение директрисы d параболы имеет вид 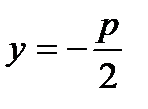 (рис. 4.9).
(рис. 4.9).
| F |
| d |
| y |
| х |
| y |
| O |
| F |
| x |
| O |
| d |
Рис. 4.8 Рис. 4.9
Пример 9. Запишите уравнение параболы, если фокус имеет координаты  .
.
Решение. 1. Так как фокус параболы расположен на оси абсцисс, то уравнение параболы имеет вид  .
.
2. Так как фокус имеет координаты  , то
, то  , а
, а  .
.
3. Запишем уравнение параболы:  .
.
Ответ:  .
.
Контрольный тест 4
Укажите правильный вариант ответа (1 – 10):
1. Если прямая пересекает оси координат в точках  и
и
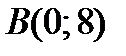 , то ее уравнение с угловым коэффициентом имеет вид
, то ее уравнение с угловым коэффициентом имеет вид
Варианты ответов: 1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ; 5)
; 5)  .
.
2. Если прямая проходит через точки  и
и  , то уравнение этой прямой в общем виде записывают
, то уравнение этой прямой в общем виде записывают
Варианты ответов: 1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ; 5)
; 5)  .
.
3. Если угловой коэффициент прямой, проходящей через точку  , равен 5, то уравнение этой прямой в отрезках имеет вид
, равен 5, то уравнение этой прямой в отрезках имеет вид
Варианты ответов: 1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ; 5)
; 5)  .
.
4. Даны прямые:
 ; ;
| (1) | 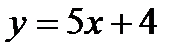 ; ;
| (2) |
 ; ;
| (3) |  ; ;
| (4) |
 . .
| (5) |
Параллельными являются прямые
Варианты ответов: 1) (1), (3) и (5); 2) (1) и (2); 3) (2) и (5);
4) (1), (3), (4) и (5); 5) (3) и (4).
5. Даныпрямые:
 ; ;
| (1) |  ; ;
| (2) |
 ; ;
| (3) | 
| (4) |
Перпендикулярными являются прямые
Варианты ответов: 1) (1) и (2); 2) (1) и (3); 3) (2) и (3);
4) (3) и (4); 5) (2) и (4).
6. Сумма расстояний от точки  до прямых
до прямых  и
и  равна
равна
Варианты ответов: 1) 8; 2) 5; 3) 1,5; 4) 3,25; 5) 4,5.
7. Если уравнение окружности имеет вид  , то сумма координат точки, которая является ее центром, равна
, то сумма координат точки, которая является ее центром, равна
Варианты ответов: 1) 3; 2) – 3; 3) – 15; 4) 15; 5) 0.
8. Если эллипс пересекает ось Ox в точках  и
и  , а ось Oy в точках
, а ось Oy в точках  и
и  , то его фокусы находятся в точках
, то его фокусы находятся в точках
Варианты ответов: 1)  ,
,  ;
;
2)  ,
,  ; 3)
; 3)  ,
, 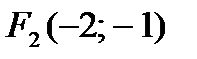 ;
;
4)  ,
,  ; 5)
; 5)  ,
,  .
.
9. Если гипербола проходит через точки  и
и  , причем длина ее мнимой полуоси b в 2 раза меньше длины действительной полуоси a, то значение выражения
, причем длина ее мнимой полуоси b в 2 раза меньше длины действительной полуоси a, то значение выражения  равно
равно
Варианты ответов: 1) 9; 2) 4; 3) 3,5; 4) 7,5; 5) 4,5.
10. Если уравнение параболы имеет вид  , то ее фокус находится в точке, сумма координат которой, увеличенная в 2 раза, равна
, то ее фокус находится в точке, сумма координат которой, увеличенная в 2 раза, равна
Варианты ответов: 1) 2,5; 2) 5; 3) 10; 4) 20; 5) 25.