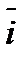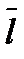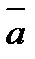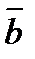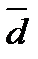Чтобы решить систему линейных уравнений методом Гаусса, необходимо:
1) составить расширенную матрицу системы;
2) с помощью элементарных преобразований привести ее к трапециевидному виду;
3) на основе полученной матрицы составить и решить систему линейных уравнений;
Чтобы привести матрицу к треугольному виду, можно выполнять следующие элементарные преобразования этой матрицы:
1) умножать и делить ее любою строку на отличное от нуля число;
2) менять местами строки;
3) складывать и вычитать строки;
4) вычеркивать строки, все элементы в которых нули.
Пример 3. Найдите решение системы линейных уравнений 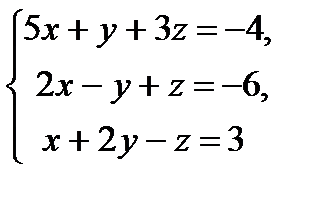 методом Гаусса.
методом Гаусса.
Решение. Запишем расширенную матрицу системы:
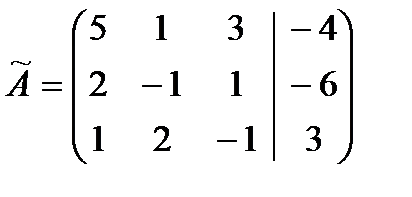 .
.
С помощью элементарных преобразований приведем ее к трапециевидному виду:
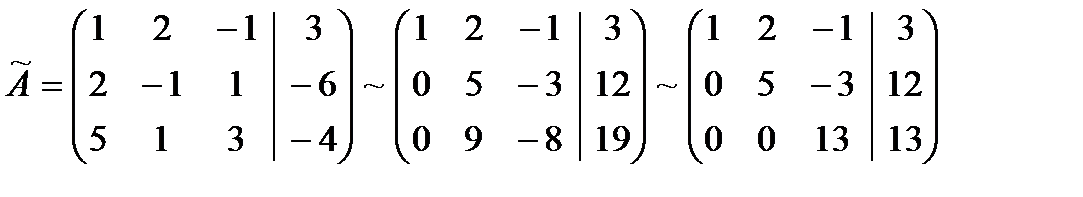 .
.
Решим систему уравнений: 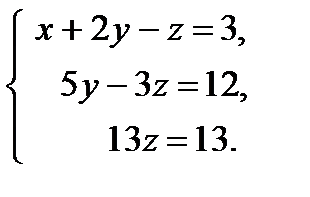
Получим:  ,
,  ,
,  .
.
Проверка: 
Ответ:  ,
, 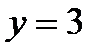 ,
, 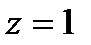 .
.
Пример 4. Решите систему линейных уравнений 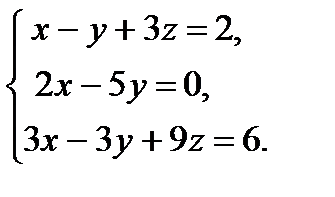
Решение. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к трапециевидному виду:
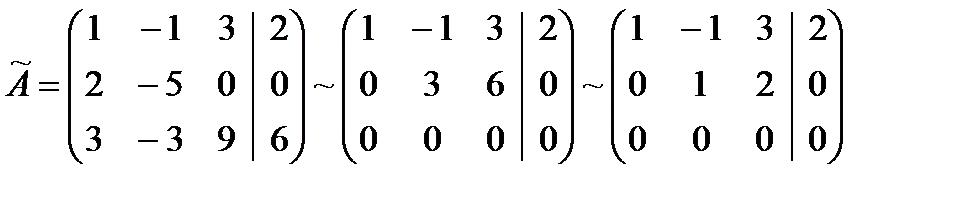 .
.
Запишем систему уравнений, соответствующую трапециевидной матрице: 
Полагая 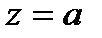 , где
, где 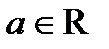 , получим:
, получим: 
Тогда 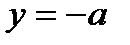 , а
, а 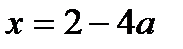 .
.
Ответ:  ,
, 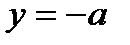 ,
, 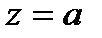 , где
, где 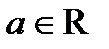 .
.
Контрольный тест 2
Укажите правильный вариант ответа (1 – 10):
1. Если 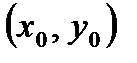 – решение системы линейных уравнений
– решение системы линейных уравнений
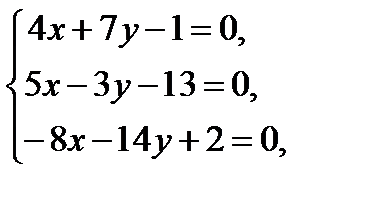
то значение выражения 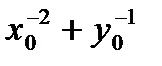 равно
равно
Варианты ответов: 1) 1,25; 2) 1; 3) 20; 4) 0,5; 5) – 0,75.
2. Система линейных уравнений

имеет следующее решение
Варианты ответов: 1)  ;
; 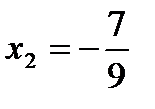 ;
;  ;
;
2) 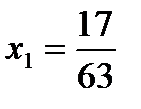 ;
; 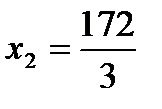 ;
; 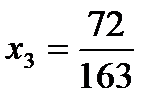 ; 3)
; 3) 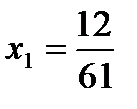 ;
; 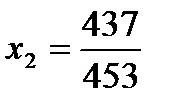 ;
;  ;
;
4) 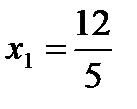 ;
;  ;
; 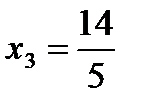 ; 5)
; 5)  ;
;  ;
;  .
.
3. Сумма всех значений переменных, которые образуют решение системы уравнений
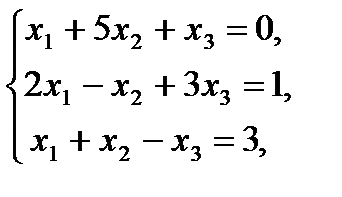
равна
Варианты ответов: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 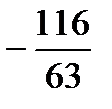 .
.
4. Если 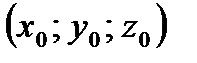 – решение системы уравнений
– решение системы уравнений
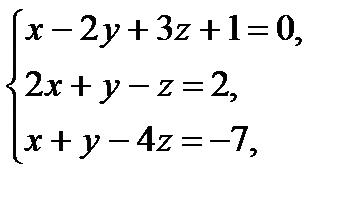
то значение 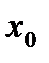 равно
равно
Варианты ответов: 1) 5; 2) 3; 3) 1; 4) – 1; 5) 0.
5. Если  – решение системы уравнений
– решение системы уравнений

то значение  равно
равно
Варианты ответов: 1) 0; 2) – 3; 3) – 51; 4) 1; 5) 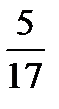 .
.
6. Если 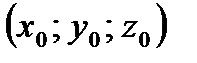 – решение системы уравнений
– решение системы уравнений
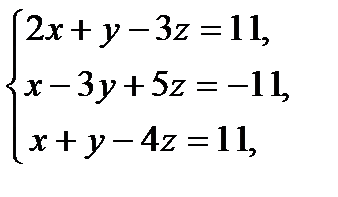
то значение 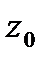 равно
равно
Варианты ответов: 1) 15; 2) – 11; 3) 0; 4) – 2; 5) 11.
7. Если 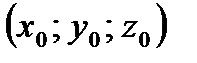 – решение системы уравнений
– решение системы уравнений
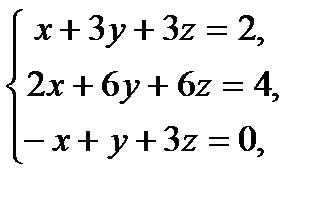
то значение выражения  равно
равно
Варианты ответов: 1) 0; 2)  ; 3) 1; 4) 12; 5)
; 3) 1; 4) 12; 5)  , где
, где  .
.
8. Если  – определитель основной матрицы системы уравнений
– определитель основной матрицы системы уравнений 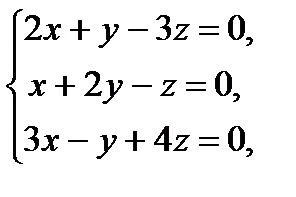 а
а 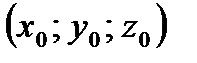 – ее решение, то значение выражения
– ее решение, то значение выражения 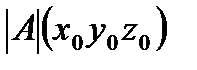 равно
равно
Варианты ответов: 1) 28; 2) 34; 3) 17; 4) – 14; 5) 0.
9. Система уравнений 
1) совместная;
2) не совместная;
3) определенная;
5) не определенная.
10. Сумма модулей всех значений переменных, которые образуют решение системы линейных уравнений
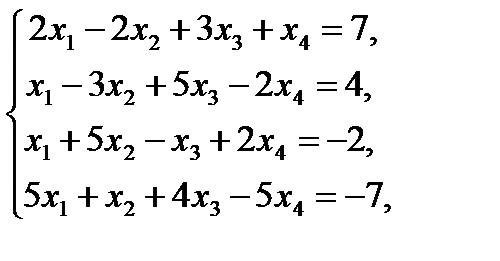
равна
Варианты ответов: 1) 2; 2) 8; 3) 28; 4) 4; 5) 0.
ВЕКТОРЫ
Основные понятия и определения
Вектором называют направленный отрезок. Начало и конец вектора обозначают двумя прописными буквами латинского алфавита или одной строчной буквой и записывают: 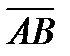 или
или  .
.
| На рисунке 3.1 изображен вектор 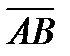 , у которого точка А – начало, а точка В – его конец, и вектор , у которого точка А – начало, а точка В – его конец, и вектор  , у которого точка С – его начало, а точка D – его конец. , у которого точка С – его начало, а точка D – его конец.
| ||||||
| Рис. 3.1 |
Нуль – вектором называют вектор, начало и конец которого совпадают. Нуль-вектор изображают точкой и записывают 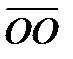 (рис. 3.1).
(рис. 3.1).
Единичным вектором называют вектор, длина которого равна единице.
Рассмотрим двумерное пространство с заданной в нем системой координат (рис. 3.2). На оси Ох отложим единичный вектор  , начало которого совпадает с началом отсчета, а направление – с положительным направлением оси Ох. Аналогичным образом отложим на оси Оу вектор
, начало которого совпадает с началом отсчета, а направление – с положительным направлением оси Ох. Аналогичным образом отложим на оси Оу вектор 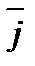 . Векторы
. Векторы  и
и  называют координатными векторами (ортами) прямоугольной системы координат. Любой вектор
называют координатными векторами (ортами) прямоугольной системы координат. Любой вектор 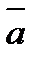 на плоскости можно разложить по ортам:
на плоскости можно разложить по ортам:
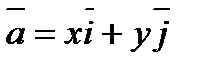 .
.
Говорят, что х и у – координаты вектора 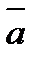 и записывают:
и записывают:
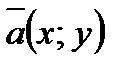 .
.
Вектор, начало которого совпадает с началом отсчета, называют радиус-вектором. На рисунке 3.2 вектор 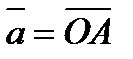 – радиус-вектор.
– радиус-вектор.
|
| |||||||||||||||||||
| Рис. 3.2 | Рис. 3.3 |
Рассмотрим трехмерное пространство с заданной в нем декартовой системой координат (рис. 3.3). Единичные векторы  ,
,  и
и 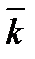 – координатные векторы (орты) прямоугольной системы координат.
– координатные векторы (орты) прямоугольной системы координат.
Любой вектор  пространства можно разложить по ортам:
пространства можно разложить по ортам:
 .
.
Говорят, что х, у и z – координаты вектора  и записывают:
и записывают:
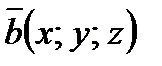 .
.
Чтобы найти координаты вектора, необходимо из координат конца вектора вычесть соответствующие координаты его начала. Если вектор 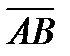 задан в двумерном пространстве, и точка
задан в двумерном пространстве, и точка 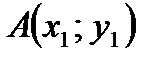 – его начало, а точка
– его начало, а точка 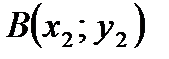 – его конец, то он имеет две координаты
– его конец, то он имеет две координаты 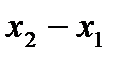 и
и  , которые записывают в круглых скобках вслед за названием вектора или без названия вектора:
, которые записывают в круглых скобках вслед за названием вектора или без названия вектора:
 или
или 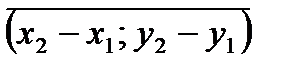 .
.
Если вектор задан в трехмерном пространстве и точка  – его начало, а точка
– его начало, а точка 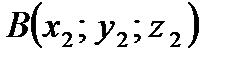 – его конец, то записывают:
– его конец, то записывают: 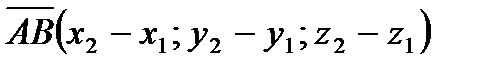 .
.
Например: 1) Если известны координаты точек 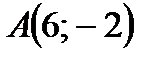 и
и  , то вектор
, то вектор 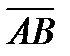 будет иметь координаты:
будет иметь координаты: 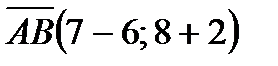 или
или 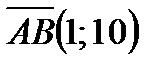 . Вектор
. Вектор 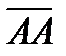 координаты:
координаты: 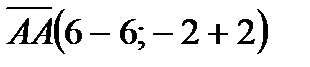 или
или 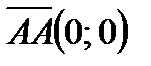 . Вектор
. Вектор  будет иметь координаты:
будет иметь координаты:  .
.
2) Если известны точки 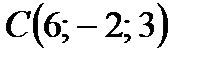 и
и 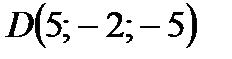 , то вектор
, то вектор 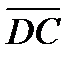 будет иметь координаты:
будет иметь координаты:
 или
или 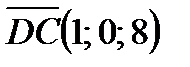 .
.
Координаты середины отрезка (середины вектора): если точки 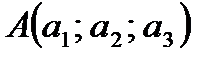 и
и 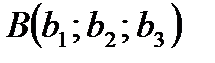 – концы отрезка, а точка М – его середина, то точка М будет иметь координаты:
– концы отрезка, а точка М – его середина, то точка М будет иметь координаты:
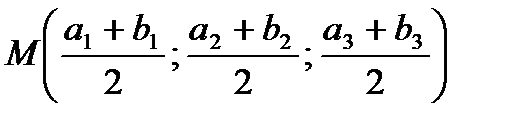 .
.
Например: 1) Если известны координаты точек 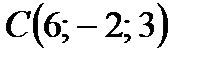 и
и 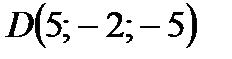 , то точка М, являющаяся серединой отрезка
, то точка М, являющаяся серединой отрезка  , будет иметь координаты:
, будет иметь координаты:
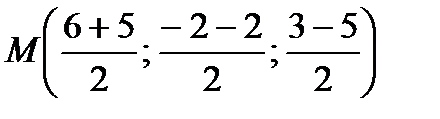 или
или 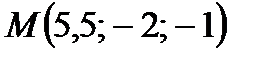 .
.
2) Если известны координаты точки  , которая является серединой отрезка АВ, и координаты точки
, которая является серединой отрезка АВ, и координаты точки  , то координаты точки
, то координаты точки 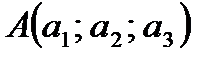 найдем, решая уравнения:
найдем, решая уравнения:
 ,
,  и
и 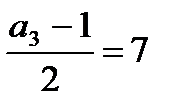 ,
,
откуда 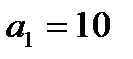 ,
, 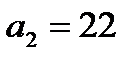 и
и 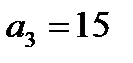 .
.
Запишем: 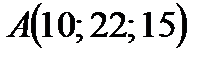 .
.
Длину вектора 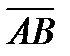 записывают
записывают  и читают: модуль вектора или длина вектора
и читают: модуль вектора или длина вектора 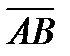 .
.
Если известны координаты точек 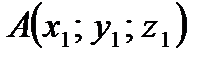 – начала и
– начала и 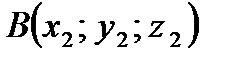 – конца вектора, то длину вектора (длину отрезка) находят по формуле:
– конца вектора, то длину вектора (длину отрезка) находят по формуле:
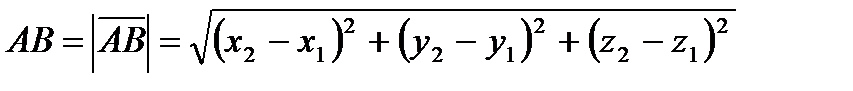 . (3.1)
. (3.1)
Если известны координаты вектора  , то длину вектора
, то длину вектора  находят по формуле:
находят по формуле:
 . (3.2)
. (3.2)
Пример 1. Известны координаты вершин треугольника ABC: 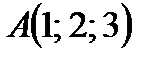 ,
,  и
и  . Найдите периметр этого треугольника.
. Найдите периметр этого треугольника.
Решение. Согласно формуле 3.1 запишем:
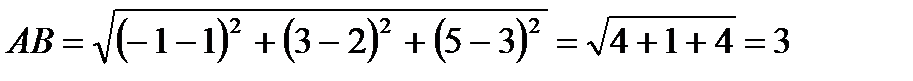 ;
;
 ;
;
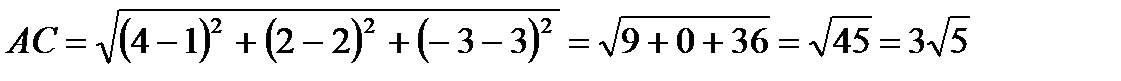 .
.
Зная длины сторон треугольника, найдем его периметр:
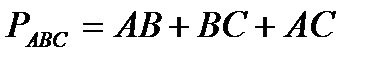 ,
, 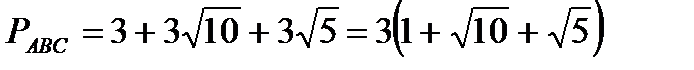 .
.
Ответ: 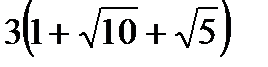 .
.
Пример 2. Найдите длину вектора 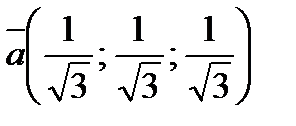 .
.
Решение. Согласно формуле 3.2 запишем: 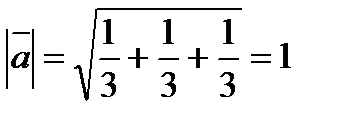 . Поскольку длина вектора
. Поскольку длина вектора  равна единице, вектор
равна единице, вектор  – единичный.
– единичный.
Ответ: 1.
Коллинеарными называют векторы, лежащие на параллельных прямых (или на одной прямой).
| На рисунке 3.4 изображены коллинеарные векторы  , ,  , ,  и и  . .
| ||||
| Рис. 3.4 |
Условие коллинеарности векторов: векторы  и
и  коллинеарны, если их соответствующие координаты пропорциональны, то есть если выполняется равенство
коллинеарны, если их соответствующие координаты пропорциональны, то есть если выполняется равенство
 . (3.3)
. (3.3)
При этом, если:
а)  , то векторы сонаправлены;
, то векторы сонаправлены;
б)  , то векторы противоположно направлены.
, то векторы противоположно направлены.
Например: 1) На рисунке 3.4 векторы  и
и 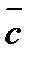 , а также
, а также 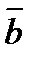 и
и  сонаправлены. Записывают:
сонаправлены. Записывают: 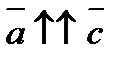 и
и  .
.
2) На рисунке 3.4 вектор  и
и  , а также векторы
, а также векторы 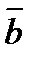 и
и 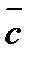 противоположно направлены. Записывают:
противоположно направлены. Записывают:  и
и 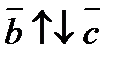 .
.
3) Векторы 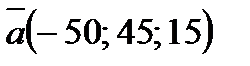 и
и  коллинеарны, так как
коллинеарны, так как  . А поскольку
. А поскольку  , то они противоположно направлены.
, то они противоположно направлены.
Векторы, имеющие равные длины и противоположно направленные, называют противоположными.
| Вектор, противоположный вектору  , записывают: , записывают: 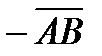 или или  .
А вектор, противоположный вектору .
А вектор, противоположный вектору  , записывают: , записывают: 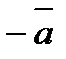 (рис. 3.5). (рис. 3.5).
| ||||
| Рис.3.5 |
Например, векторы 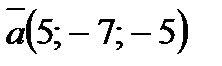 и
и 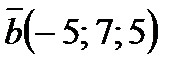 противоположны, так как
противоположны, так как  ,
,  и
и 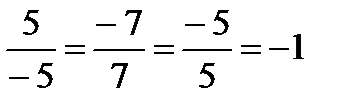 .
.
Векторы, лежащие в параллельных плоскостях (или в одной плоскости), называют компланарными
| На рисунке 3.6 изображен прямой параллелепипед. Векторы 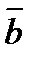 , , 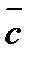 и и  , а также векторы , а также векторы  , , 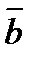 и и  компланарны. Векторы компланарны. Векторы 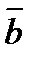 , , 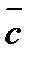 и и 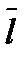 , а также векторы , а также векторы  , , 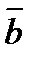 и и 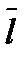 не компланарны. не компланарны.
| ||||||
| Рис. 3.6 |
Условие компланарности трех векторов: векторы  ,
,  и
и 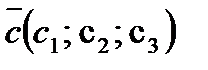 компланарны, если определитель, составленный из координат этих векторов, равен нулю:
компланарны, если определитель, составленный из координат этих векторов, равен нулю:
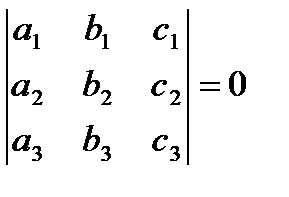 (3.4)
(3.4)