4.1 Цель работы
Закрепление и углубление знаний и приобретение практических навыков в области проведения и оценки результатов прямых многократных измерений.
4.2 Содержание работы
Проведение прямых многократных измерений одной и той же заданной физической величины (номинального значения сопротивления), обработка экспериментальных данных с целью построения гистограммы распределения случайной величины и оценки результата измерений.
4.3 Экспериментальное оборудование
Омметр, резисторы.
4.4 Подготовка к работе
Самостоятельная подготовка студентов к выполнению лабораторной работы осуществляется по следующим разделам:
– погрешности измерений [2, 14];
– основной постулат метрологии [1, 17];
– точечные и интервальные оценки результата измерений [1, 14];
– обработка экспериментальных данных при проведении многократных измерений [5].
4.5 Теоретическая часть
Гистограмма – это серия столбиков одинаковой ширины, но разной высоты, показывающая рассеяние и распределение данных. Ширина столбика – это интервал в диапазоне наблюдений, высота – количество данных, приходящихся на тот или иной интервал, т.е. частота. По существу, гистограмма отображает распределение исследуемого показателя. Гистограмма позволяет оценить характер рассеивания показателя и разобраться в том, на чём следует сосредоточить усилия по улучшению.
Характерные типы гистограмм показаны на рис. 4.1.

Рисунок 4.1 – Характерные типы гистограмм
На рисунке 4.1,а показан обычный тип гистограммы с двусторонней симметрией, что указывает на стабильность процесса.
На рисунке 4.1,б в распределении имеется два пика (двугорбая гистограмма). Такая гистограмма получается при объединении двух распределений, например, в случае двух видов сырья, изменения настройки процесса или объединения в одну партию изделий, обработанных на двух разных станках. Требуется расслоение продукции.
На рисунке 4.1,в показана гистограмма с обрывом. Такое распределение получается, когда невозможно получить значение ниже (или выше) некоторой величины. Подобное распределение имеет место также, когда из партии исключены все изделия с показателем ниже (и/или выше) нормы, т.е. изначально это была партия с большим количеством дефектных изделий. Такое же распределение получается, когда измерительные приборы были неисправны.
На рисунке 4.1,г показана гистограмма с островком. Получается при ошибках в измерениях, или когда некоторое количество дефектных изделий перемешано с доброкачественными.
На рисунке 4.1,д показана гистограмма с прогалами («гребёнка»). Получается, когда ширина интервала не кратна единице измерения или при ошибках оператора.
На рисунке 4.1,е показана гистограмма в форме плато. Получается, когда объединяются несколько распределений при небольшой разнице средних значений. В этом случае требуется расслоение.
Достоинства метода:
– Наглядность, простота освоения и применения.
– Управление с помощью фактов, а не мнений.
– Позволяет лучше понять вариабельность, присущую процессу, глубже взглянуть на проблему и облегчить нахождение путей ее решения.
Недостатки метода:
– Интерпретация гистограммы, построенная по малым выборкам, не позволяет сделать правильные выводы.
Пример. При п -кратном независимом измерении одной и той же физической величины постоянного размера аналоговым измерительным прибором указатель отсчетного устройства в случайной последовательности по m раз останавливался на каждом из делений шкалы, показания прибора приведены в таблице 2. Чему равен отсчет при таком измерении?
Принимаем деления шкалы за основания и построим на них прямоугольники с высотами, равными отношениям частоты М/п к цене деления ∆ х.
 Таблица 2 – Показания прибора
Таблица 2 – Показания прибора
| Деление шкалы | m | Деление шкалы | m |
| 0,1…0,11 | 0,15…0,16 | ||
| 0,11…0,12 | 0,16…0,17 | ||
| 0,12…0,13 | 0,17…0,18 | ||
| 0,13…0,14 | 0,18…0,19 | ||
| 0,14…0,15 | 0,19…0,20 |
Полученная фигура называется гистограммой (рису-
нок 4.2). Если соединить отрезками прямых середины верхних сторон прямоугольников, получим ломаную линию, называемую полигоном.

Рисунок 4.2 – Гистограмма и полигон аналогового
измерительного прибора
Как гистограмма, так и полигон являются исчерпывающим эмпирическим описанием отсчета.
Гистограмма – один из вариантов столбиковой диаграммы, позволяющий зрительно оценить распределение статистических данных, сгруппированных по частоте попадания в определенный (заранее заданный) интервал.
Если на контролируемый параметр существует поле допуска, то гистограмма может содержать верхнюю и нижнюю границы поля допуска (рисунок 4.3). Это позволяет увидеть в какую сторону и как смещается значение контролируемого показателя относительно поля допуска. Границы наносятся по оси абсцисс.

Рисунок 4.3 – Гистограмма контролируемого параметра,
имеющего допуск
Для осмысления качественных характеристик изделий, процессов, производства (статистических данных) и наглядного представления тенденции изменения наблюдаемых значений применяют графическое изображение статистического материала, т.е. строя гистограмму распределения.
Если бы была возможность увеличивать п, то в пределе при
п → ∞ и ∆ х → 0 полигон преобразовался бы в плавную кривую – кривую плотности распределения вероятности отсчета p(x) (дифференциальная функция распределения)(рисунок 4.4).

Рисунок 4.4 – Плотность распределения вероятности отсчета
Можно было бы построение выполнить иначе. Подсчитывая, сколько раз указатель отсчетного устройства останавливался левее каждой отметки шкалы, откладывая над этой отметкой вдоль оси ординат отношение числа таких отклонений к их общему числу п и соединяя полученные точки отрезками прямых, мы получим ломаную линию, называемую кумулятивной кривой (рисунок 4.5, а). При п →∞ кумулятивная кривая преобразуется в функцию распределения вероятности отсчета F(x) (рисунок 4.5, б).

Рисунок 4.5 – Для аналогового измерительного прибора:
а – кумулятивная кривая; б – функция распределения вероятности отсчета
Плотность распределения вероятности p(x) и функция распределения вероятности F(x) служат математическими моделями законов распределения, получаемых из экспериментальных данных.
Рассмотрим некоторые основные свойства законов распределения вероятности отсчета:
1. Функция распределения вероятности F(x) определяет вероятность того, что отдельный результат сравнения будет меньше x.
2. F(x) – функция неубывающая, т.е. чем больше x, тем больше вероятность того, что результат сравнения не превысит это значение. При этом в случае изменения x от –∞ до ∞ F(x) изменяется от нуля до единицы.
3. Вероятность того, что результат сравнения окажется в интервале от x1 до x 2, равна разности значений F(x) на границах этого интервала:  и
и  .
.
Описание отсчета с помощью законов распределения вероятностей является наиболее полным, но неудобным. Обычно ограничиваются приближенным описанием закона с помощью его числовых характеристик или моментов. Все они представляют собой некоторые средние значения. Если величины усредняются относительно начала координат, то они называются начальными, если усреднение производится относительно центра распределения, то моменты называются центральными.
Общее правило образования начальных моментов:
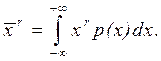
В метрологии широкое распространение находит начальный момент первого порядка, который называют математическим ожиданием или средним значением отсчета:

Свойства математического ожидания:

 ;
;
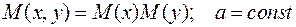 .
.
Математическое ожидание характеризует среднее значение отсчета, при этом экспериментально определить М(х) не представляется возможным, поскольку для этого необходимо осуществить бесконечное число измерений. На практике используют лишь оценку математического ожидания, в качестве которой используется среднее арифметическое. Можно легко показать, что среднее арифметическое при n →∞ стремится к математическому ожиданию.
Мерой рассеяния результатов сравнения по формуле относительно среднего значения является центральный момент второго порядка, который называют дисперсией:

Свойства дисперсии: D(a) = 0; D(ax) = a2D(x);
D(x+y) = D(x) + D(y); a = const.
Чем больше дисперсия, тем значительнее рассеяние результатов сравнения относительно  . Это наглядно демонстрируют кривые плотности распределения вероятности отсчета при различных дисперсиях (рисунок 4.6).
. Это наглядно демонстрируют кривые плотности распределения вероятности отсчета при различных дисперсиях (рисунок 4.6).

Рисунок 4.6 – Кривые плотности распределения
вероятности отсчета при различных дисперсиях
В метрологии в качестве меры рассеяния чаще используют среднее квадратическое отклонение.
Среднее квадратическое отклонение, как и математическое ожидание, будучи характеристикой случайных законов распределения, само не является случайным, что очень удобно.
Однако найти его также невозможно опытным путем, и ограничиваются определением оценки среднего квадратического отклонения по формуле
 .
.
Математическими моделями эмпирических законов распределения вероятности отсчета могут быть различные законы распределения, например закон Симпсона, Релея, нормальный закон распределения, равномерный и т.д.
Нормальный закон распределения (закон Гаусса) является наиболее распространенным при описании эмпирических данных. Кривая распределения для нормального закона имеет колоколообразную форму (рисунок 4.7).

Рисунок 4.7 – Нормальный закон распределения
Для определения дифференциальной и интегральной функций распределения используются формулы:
 ;
;  .
.
К важнейшим преимуществам нормального закона распределения относится то, что он является устойчивым, т.е. при комбинации нормальных законов получается также нормальный закон. Вторым важным преимуществом является наличие различных табулированных данных по этому закону, что существенно упрощает процедуру его применения.
Закон равномерного распределения имеет место, когда вероятность появления отсчета на некотором интервале значений измеряемой величины остается неизменной (пример с технологическим распределением сопротивлений резисторов, распределением диаметров шариков в подшипнике).
В метрологии находит также широкое применение центрированный закон равномерного распределения. Равномерным распределением называют такое распределение случайной величины, когда она с одинаковой вероятностью может принимать любое значение в заданных пределах (рисунок 4.8).

Рисунок 4.8 – Плотность вероятности (дифференциальная функция)
равномерного распределения
Плотность вероятности равномерного распределения имеет вид:
 при
при  ;
;  при
при  ;
;  при
при  ,
,
где  и
и  – параметры закона, определяющие пределы изменения случайной величины
– параметры закона, определяющие пределы изменения случайной величины  .
.
Закону равномерного распределения подчиняются погрешности от трения в опорах приборов, дискретности в цифровых приборах и т.д.
Математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины, подчиняющейся равномерному распределению, соответственно равны:
 ;
; 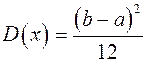 ;
;  .
.
Практически предельное поле рассеивания  при равномерном распределении равно:
при равномерном распределении равно:  =
=  или
или  .
.
Погрешность средства измерения, возникающая в результате влияния целого ряда факторов, является всегда величиной случайной. Часто погрешность имеет некоторую закономерную составляющую, приводящую к смещению среднего значения показания относительно значения измеряемой величины, т.е. СИ дает постоянно завышенные или заниженные показания. Указанная закономерная составляющая погрешности СИ, которую ранее называли систематической погрешностью, может при повторных измерениях одной и той же величины оставаться неизменной или изменяться по определенному закону. В соответствии с характером зависимости закономерной погрешности от измеряемой величины она может именоваться постоянной (например, смещение начала отсчета); прогрессивной (погрешность градуировки шкалы, погрешность при измерении времени); периодической (погрешность от эксцентриситета шкалы).
Рассеяние отдельных значений результата измерения объясняется тем, что сравнение неизвестного размера с известным (получение отсчета) происходит в условиях воздействия множества случайных факторов (помех), точный учет совместного влияния которых невозможен. Поэтому для оценки закона распределения результата измерения необходимо провести многократное измерение, т.е. несколько раз измерить одну и ту же величину.
Применяют два вида оценок результата измерения.
1) Точечные оценки.
Точечными называют оценки, которые выражаются одним числом. Предположим, что путем внесения поправок все закономерно изменяющиеся факторы учтены (выполнено исправление результата измерения). Тогда результат каждого отдельного сравнения при многократном измерении можно представить как
 ,
,
где  – случайная погрешность результата измерения; Q – значение измеряемой величины.
– случайная погрешность результата измерения; Q – значение измеряемой величины.
В большинстве случаев случайная величина Qi распределена по одному из симметричных законов (как правило, по нормальному закону). Определим среднее арифметическое значение результата измерения:
 .
.
Для симметричных законов при достаточно большом n  , т.е. среднее арифметическое стремится к значению измеряемой величины:
, т.е. среднее арифметическое стремится к значению измеряемой величины:  .
.
Вывод: при симметричных законах распределения вероятности результата измерения среднее арифметическое, будучи оценкой математического ожидания, является оценкой истинного значения измеряемой величины.
Мерой рассеяния отдельных результатов сравнения относительно среднего арифметического является среднее квадратическое отклонение, оценка которого определяется как
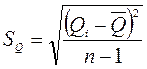 .
.
Среднее квадратическое является мерой случайной погрешности однократного измерения.
Среднее арифметическое находится по конечному ряду значений, каждое из которых – случайная величина. Поэтому среднее арифметическое, будучи оценкой результата измерения, также случайная величина.
Мерой рассеяния среднего арифметического относительно значения измеряемой величины служит среднее квадратическое отклонение среднего арифметического или так называемое стандартное отклонение, оценка которого определяется как
 .
.
Стандартное отклонение является мерой случайной погрешности многократного измерения.
С увеличением числа опытов при многократном измерении точность последнего возрастает в  раз (семь раз отмерь – один раз отрежь).
раз (семь раз отмерь – один раз отрежь).
2) Интервальные оценки.
Точечные оценки Q и S характеризуют результат измерения, однако оценка по данным точечным характеристикам результата измерения не является наглядной и не дает непосредственной информации о том, чему же равно значение измеряемой величины.
Смысл оценки результата измерения с помощью интервалов заключается в нахождении доверительных интервалов, между границами которых с определенной вероятностью (доверительной) находится значение измеряемой величины.
Пусть α означает вероятность того, что значение результата измерения не отличается от значения величины больше, чем на Е, это можно записать
 ,
,
где  – доверительная вероятность;
– доверительная вероятность;
интервал значений от  до
до  – доверительный интервал.
– доверительный интервал.
Следовательно, доверительный интервал и доверительная вероятность связаны между собой: чем больше α, тем больше должен
быть Е. Таким образом, для оценки результата измерения необходимо иметь два значения: доверительный интервал – оценку точности и доверительную вероятность – оценку надежности результата.
На практике задаются определенной степенью надежности (доверительной вероятностью) и рассчитывают доверительный интервал. В машиностроении и приборостроении задаются α = 90...95 %, хотя для ответственных изделий может иметь место 0,99 % и даже 0,999 %.
Значение Е определяется на основании точечных оценок. Если закон распределения результата измерения нормальный, то Е можно определить с помощью табулированной функции  , где x = E / S.
, где x = E / S.
Так, например, доверительной вероятности 0,683 соответствует доверительный интервал ±S, вероятности 0,954 – интервал ± 2 S, а вероятности 0,997 – интервал ± 3 S.
Приведенные рассуждения правомочны, если имеется достаточно большое число экспериментальных данных (n > 40...50). При технических измерениях, как правило, производится значительно меньшее число измерений. В случае, когда вероятность результата распределяется по нормальному закону, а количество экспериментальных данных меньше 30...40, среднее арифметическое подчиняется закону распределения вероятности Стьюдента (псевдоним В.С. Госсета) с тем же средним значением  .
.
Не останавливаясь на математических выражениях для распределения Стьюдента, следует отметить, что значения функции также табулированы. На основании табличных данных задаются доверительной вероятностью и числом tα. Параметр (коэффициент) tα играет в метрологии важную роль, он показывает, на какое среднеквадратическое отклонение с заданной вероятностью может отличаться случайное число, подчиняющееся нормальному закону распределения вероятности, от своего среднего значения. В данном случае tα показывает, на какое среднеквадратическое отклонение среднее арифметическое может отличаться от значения измеряемой величины. Таким образом, доверительный интервал определяется как Е = tα∙S.
В отличие от нормального распределения распределение Стьюдента дает значение tα в зависимости от n. Так, например, доверительный интервал ± 2 S имеет место для доверительной вероятности 0,86 (n = 4); 0,90 (n = 6); 0,924 (n =10); 0,940 (n = 20). При n > 30 закон Стьюдента преобразуется в нормальный закон распределения.
4.6 Контрольные вопросы
1. Что такое истинное, действительное и измеренное значения измеряемой величины?
2. Что представляет собой погрешность измерения?
3. В чем заключается сущность основного постулата метрологии?
4. Можно ли получить результат измерений без погрешности?
5. Перечислите основные точечные оценки результата измерения. Что характеризует каждая из оценок?
6. Что показывают доверительный интервал и доверительная вероятность при оценке истинного значения величины?
7. Что необходимо знать для определения доверительного интервала?
8. Что такое закон распределения случайной величины?
9. Что такое гистограмма? Изложите методику построения гистограмм.
10. Как записывается итог измерения при точечных оценках и оценках с помощью интервалов?
4.7 Порядок выполнения работы
1. Ознакомиться с техническим описанием и инструкцией по эксплуатации омметра.
2. Получить у преподавателя объект измерений.
3. Оценить необходимость внесения поправки  в показания микроскопа (наличие систематической составляющей погрешности).
в показания микроскопа (наличие систематической составляющей погрешности).
4. Собрать данные, выявить максимальное и минимальное значения и определить диапазон (размах) гистограммы.
5. Полученный диапазон разделить на интервалы, предварительно определив их число (обычно 5-20 в зависимости от числа показателей) и определить ширину интервала.
6. Все данные распределить по интервалам в порядке возрастания: левая граница первого интервала должна быть меньше наименьшего из имеющихся значений.
7. Подсчитать частоту каждого интервала.
8. Вычислить относительную частоту попадания данных в каждый из интервалов.
9. По полученным данным построить гистограмму – столбчатую диаграмму, высота столбиков которой соответствует частоте или относительной частоте попадания данных в каждый из интервалов:
– наносится горизонтальная ось, выбирается масштаб и откладываются соответствующие интервалы;
– затем строится вертикальная ось, на которой также выбирается масштаб в соответствии с максимальным значением частот.
10. Уточните построенную гистограмму с учетом рисунка 4.3 для контролируемого параметра, имеющего допуск.
11. Запишите результат многократного измерения с ипотльзованием точечных и интервальных оценок.

Рисунок 4.8 – Гистограмма (нормальное распределение)
Дополнительная информация:
– Структуру вариаций легче увидеть, когда данные представлены графически в виде гистограммы.
– Прежде чем сделать выводы по результатам анализа гистограмм, убедитесь, что данные представительны для существующих условий процесса.
– Не делайте выводов, основанных на малых выборках. Чем больше объем выборки, тем больше уверенность в том, что три важных параметра гистограммы – ее центр, ширина и форма – представительны для всего процесса или группы продукции.
– Для каждой структуры вариаций (типа распределения) существуют свои интерпретации.
– Интерпретация гистограммы – это всего лишь теория, которая должна быть подтверждена дополнительным анализом и прямыми наблюдениями за анализируемым процессом.
Обычно построение гистограммы состоит из нескольких этапов:
1. Расчет размаха R из n результатов измерений (размах – это разница между наибольшим Хmax и наименьшим Xmin значениями)
 .
.
2. Определение количества интервалов k по формуле
k = 1 + 3,3× lg n
или по упрощенной формуле
k =  (3.13)
(3.13)
Полученное значение k можно округлить. Обычно 6<k<20.
3. Вычисление ширины интервалов гистограммы h
h =  . (3.14)
. (3.14)
4. Расчет границ интервалов. Границы интервалов выбирают обычно таким образом, чтобы они не совпадали с результатами измерений и крайние интервалы были заполнены.
5. Подсчет числа попаданий результатов в интервалы. Полученные результаты сводят в таблицу.
6. Построение столбчатой гистограммы.
Если полученная гистограмма соответствует «колоколу» Гаусса, то результаты измерений распределены по нормальному закону.
Пример. 50-кратные измерения напряжения (В) дали результаты, приведенные ниже. Необходимо определить закон распределения результатов измерения, построив гистограмму.
| 20,62 | 20,40 | 20,60 | 20,53 | 20,45 | 20,65 | 20,59 | 20,70 | 20,60 | 20,60 |
| 20,64 | 20,58 | 20,80 | 20,60 | 20,57 | 20,60 | 20,70 | 20,60 | 20,60 | 20,60 |
| 20,46 | 20,60 | 20,75 | 20,51 | 20,70 | 20,75 | 20,55 | 20,60 | 20,55 | 20,42 |
| 20,48 | 20,66 | 20,52 | 20,58 | 20,73 | 20,73 | 20,57 | 20,55 | 20,65 | 20,60 |
| 20,66 | 20,67 | 20,67 | 20,70 | 20,58 | 20,60 | 20,50 | 20,50 | 20,80 | 20,50 |
Рассчитаем размах результатов R по формуле
R = 20,80 – 20,40 = 0,40 В.
Определим количество интервалов по формуле:
k = 1 +3,3× lg 50 = 6,6 » 7.
По формуле (3.14) вычислим ширину интервалов
h =  В
В
Далее составим таблицу, в которую запишем границы интервалов и частоту попадания результатов в указанные интервалы (табл. 3.4). Наименьший результат измерения 20,40 В, поэтому нижнюю границу первого интервала целесообразно выбрать равной
20,40 -  = 20,37 В
= 20,37 В
Чтобы границы интервалов не совпадали с результатами, добавим к ним один разряд.
Таблица 3.4 – Расчет гистограммы
| Границы интервалов, В | Частота попадания в интервалы, hm | Относительная частота, hm/n |
| 20,375 – 20,435 | 0,04 | |
| 20,435 – 20,495 | 0,06 | |
| 20,495 – 20,555 | 0,14 | |
| 20,555 – 20,615 | 0,42 | |
| 20,615 – 20,675 | 0,12 | |
| 20,675 – 20,735 | 0,12 | |
| 20,735 – 20,795 | 0,06 | |
| 20,795 – 20,855 | 0,04 | |
| Итого | n = 50 | Р = 1,00 |
Строим гистограмму. По оси абсцисс откладываем границы интервалов, а по оси ординат – абсолютные или относительные частоты.
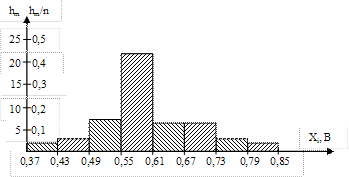
Рисунок 4.8 – Гистограмма