Дифракция на щели. Дифракционная решетка

ДИФРАКЦИЯ СВЕТА

Основные формулы

• Радиус k- ой. зоны Френеля:

для сферической волны

,

где а — расстояние диафрагмы с круглым отверстием от точечного источника света; b — расстояние диафрагмы от экрана, на котором ведется наблюдение дифракционной картины; k — номер зоны Фре­неля; λ — длина волны;

для плоской волны

.

• Дифракция света на одной щели при нормальном падении лучей. Условие минимумов интенсивности света

, k =1,2,3,…,

где а — ширина щели; φ— угол дифракции; k — номер минимума;

λ — длина волны.

Условие максимумов интенсивности света

, k =l, 2, 3,…,

где φ' — приближенное значение угла дифракции.

• Дифракция света на дифракционной решетке при нормальном падении лучей. Условие главных максимумов интенсивности

d sinφ=± k λ, k =0,1,2,3,…,

где d — период (постоянная) решетки; k — номер главного макси­мума; φ —угол между нормалью к поверхности решетки и нап­равлением дифрагированных волн.

• Разрешающая сила дифракционной решетки

,

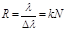где Δλ — наименьшая разность длин волн двух соседних спектраль­ных линий (λ и λ+Δλ), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; N — число штрихов решетки; k — порядковый номер дифракцион­ного максимума.

• Угловая дисперсия дифракционной решетки

,

линейная дисперсия дифракционной решетки

.

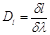Для малых углов дифракции

,

где f — главное фокусное расстояние линзы, собирающей на экра­не дифрагирующие волны.

• Разрешающая сила объектива телескопа

,

где β — наименьшее угловое расстояние между двумя светлыми точками, при котором изображения этих точек в фокальной плос­кости объектива могут быть видны раздельно; D — диаметр объек­тива; λ — длина волны.

• формула Вульфа — Брэгга

2 d sin =k λ,

где d — расстояние между атомными плоскостями кристалла; 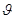— угол скольжения (угол между направлением пучка параллель­ных лучей, падающих на кристалл, и гранью кристалла), опре­деляющий направление, в котором имеет место зеркальное отраже­ние лучей (дифракционный максимум).

Примеры решения задач

Пример 1. На диафрагму с круглым отверстием радиусом r =1 мм падает нормально параллельный пучок света длиной волны λ=0,05 мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние b_max от центра от­верстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пят­но.

Решение. Расстояние, при котором будет видно темное пят­но, определяется числом зон Фре­неля, укладывающихся в отвер­стии. Если число зон четное, то в центре дифракционной картины бу­дет темное пятно.

Число зон Френеля, помещаю­щихся в отверстии, убывает по мере удаления экрана от отверстия. Наименьшее четное число зон равно двум. Следовательно, максимальное расстояние, при котором еще будет наблюдаться темное пятно в центре экрана, определяется условием, согласно которому в отверстии должны поместиться две зоны Френеля.

Из рис. 31.1 следует, что расстояние от точки наблюдения O на экране до края отверстия на 2 ( λ /2) больше, чем расстояние b_max.

По теореме Пифагора получим

.

Учтя, что λ<< b_mах и что членом, содержащим λ², можно пренеб­речь, последнее равенство перепишем в виде

r² =2λ b_max. откуда b_max =r²/(2λ). Произведя вычисления по последней формуле, найдем

b_max=1 м.

Пример 2. На щель шириной а =0,1 мм нормально падает параллельный пучок света от монохроматического источника (λ==0,6 мкм). Определить ширину l центрального максимума в дифракционной картине, проецируемой с помощью линзы, нахо­дящейся непосредственно за щелью, на экран, отстоящий от лин­зы на расстоянии L =l м.

Решение. Центральный максимум интенсивности света за­нимает область между ближайшими от него справа и слева миниму­мами интенсивности. Поэтому ширину центрального максимума интенсивности примем равной расстоянию между этими двумя минимумами интенсивности (рис. 31.2).

Минимумы интенсивности света при дифракции от одной щели наблюдаются под углами φ, определяемыми условием

a sin φ=± k λ, (1)

где k — порядок минимума; в нашем случае равен единице.

Расстояние между двумя минимумами на экране определим не­посредственно по чертежу: l=2L tgφ. Заметив, что при малых уг­лах tg φ sin φ, перепишем эту формулу в виде

/=2L sin φ. (2)

Выразим sin φ из формулы (1) и подставим его в равенство (2):

l=2Lkλ/a. (3)

Произведя вычисления по фор­муле (3), получим l =1,2 см.

Пример 3. На дифракционную решетку нормально к ее поверх­ности падает параллельный пучок света с длиной волны λ=0,5мкм. Помещенная вблизи решетки лин­за проецирует дифракционную картину на плоский экран, удаленный от линзы на L =l м. Расстоя­ние l между двумя максимумами интенсивности первого порядка, наблюдаемыми на экране, равно 20,2 см (рис. 31.3). Определить: 1) постоянную d дифракционной решетки; 2) число n штрихов на 1 см; 3) число максимумов, которое при этом дает дифракционная решетка; 4) максимальный угол φ _mах отклонения лучей, соот­ветствующих последнему дифракционному максимуму.

Решение 1. Постоянная d дифракционной решетки, длина волны λ и угол φ отклоне­ния лучей, соответствую­щий k-му дифракционному максимуму, связаны соот­ношением

dsin φ= k λ, (1)

где k — порядок спектра, или в случае монохрома­тического света порядок максимума.

В данном случае k =1, sin φ=tg φ (ввиду того, что l /2<< L), tgφ=(l /2) L (следует из рис. 31.3). С учетом последних трех равенств соотношение (1) примет вид

,

откуда постоянная решетки

d =2 L λ/ l.

Подставляя данные, получим

d =4,95 мкм.

2. Число штрихов на 1 см найдем из формулы

п =1/ d.

После подстановки числовых значений получим n =2,02-10³ см^-1.

3. Для определения числа максимумов, даваемых дифракцион­ной решеткой, вычислим сначала максимальное значение k_max исходя из того, что максимальный угол отклонения лучей решеткой не может превышать 90°.

Из формулы (1) запишем

. (2)

Подставляя сюда значения величин, получим

K_max =9,9.

Число k обязательно должно быть целым. В то же время оно не может принять значение, равное 10, так как при этом значении sin φ должен быть больше единицы, что невозможно. Следователь­но, k_mах =9.

Определим общее число максимумов дифракционной картины, полученной посредством дифракционной решетки. Влево и вправо от центрального максимума будет наблюдаться по одинаковому числу максимумов, равному k_mах, т. е. всего 2 k_mах. Если учесть также центральный нулевой максимум, получим общее число мак­симумов

N =2 k_max +l.

Подставляя значение k_mах найдем

N =2*9+1=19.

4. Для определения максимального угла отклонения лучей, соответствующего последнему дифракционному максимуму, выра­зим из соотношения (2) синус этого угла:

sinφ_max= k_max λ/ d.

Отсюда

φ_max=arcsin(k_max λ/ d).

Подставив сюда значения величин λ, d, k_mах и произведя вычис­ления, получим

φ _mах =65,4°.

Задачи

Зоны Френеля

31.1. Зная формулу радиуса k- й. зоны Френеля для сферической волны (ρ_k= 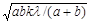), вывести соответствующую формулу для плоской волны.

31.2. Вычислить радиус ρ₅ пятой зоны Френеля для плоского волнового фронта (λ=0,5 мкм), если построение делается для точки наблюдения, находящейся на расстоянии b =1 м от фронта волны.

31.3. Радиус ρ₄ четвертой зоны Френеля для плоского волнового фронта равен 3 мм. Определить радиус ρ₆ шестой зоны Френеля.

31.4. На диафрагму с круглым отверстием диаметром d =4 мм падает нормально параллельный пучок лучей монохроматического света (λ=0,5 мкм). Точка наблюдения находится на оси отверстия на расстоянии b =1 м от него. Сколько зон Френеля укладывается в отверстии? Темное или светлое пятно получится в центре дифрак­ционной картины, если в месте наблюдений поместить экран?

31.5. Плоская световая волна (λ=0,5 мкм) падает нормально на диафрагму с круглым отверстием диаметром d =l см. На каком рас­стоянии b от отверстия должна находиться точка наблюдения, что­бы отверстие открывало: 1) одну зону Френеля? 2) две зоны Френеля?

31.6. Плоская световая волна падает нормально на диафрагму с круглым отверстием. В результате дифракции в некоторых точках оси отверстия, находящихся на расстояниях b_i, от его центра, наблю­даются максимумы интенсивности. 1. Получить вид функции b = f (r, λ, п), где r — радиус отверстия; λ — длина волны; п — чис­ло зон Френеля, открываемых для данной точки оси отверстием. 2. Сделать то же самое для точек оси отверстия, в кото­рых наблюдаются минимумы интенсивности.

31.7. Плоская световая волна (λ=0,7 мкм) падает нор­мально на диафрагму с круг­лым отверстием радиусом r =1,4 мм. Определить рас­стояния b₁, b₂, b₃ от диафраг­мы до трех наиболее удален­ных от нее точек, в которых наблюдаются минимумы интенсив­ности.

31.8. Точечный источник S света (λ=0,5 мкм), плоская диафрагма с круглым отверстием радиусом r =1 мм и экран расположены, как это указано на рис. 31.4 (а =1 м). Определить расстояние b от экра­на до диафрагмы, при котором отверстие открывало бы для точки Р три зоны Френеля.

31.9. Как изменится интенсивность в точке Р (см. задачу 31.8), если убрать диафрагму?

Дифракция на щели. Дифракционная решетка

31.10. На щель шириной а =0,05 мм падает нормально монохро­матический свет (λ=0,6 мкм). Определить угол φ между первоначаль­ным направлением пучка света и направлением на четвертую тем­ную дифракционную полосу.

31.11. На узкую щель падает нормально монохроматический свет. Угол φ отклонения пучков света, соответствующих второй светлой дифракционной полосе, равен 1°. Скольким длинам волн падающего света равна ширина щели?

31.12. На щель шириной а =0,1 мм падает нормально монохрома­тический свет (λ=0,5 мкм). За щелью помещена собирающая лин­за, в фокальной плоскости которой находится экран. Что будет на­блюдаться на экране, если угол φ дифракции равен: 1) 17'; 2) 43'.

31.13. Сколько штрихов на каждый миллиметр содержит диф­ракционная решетка, если при наблюдении в монохроматическом свете (λ=0,6 мкм) максимум пятого порядка отклонен на угол φ=18°?

31.14. На дифракционную решетку, содержащую n =100 штри­хов на 1 мм, падает нормально монохроматический свет. Зритель­ная труба спектрометра наведена на максимум третьего порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол Δφ=20°. Определить длину волны λ света.

31.15. Дифракционная решетка освещена нормально падающим монохроматическим светом. В дифракционной картине максимум второго порядка отклонен на угол φ₁=14°. На какой угол φ₂ откло­нен максимум третьего порядка?

31.16. Дифракционная решетка содержит n =200 штрихов на 1 мм. На решетку падает нормально монохроматический свет (λ=0,6 мкм). Максимум какого наибольшего порядка дает эта решетка?

31.17. На дифракционную решетку, содержащую n =400 штри­хов на 1 мм, падает нормально монохроматический свет (λ=0,6 мкм). Найти общее число дифракционных максимумов, которые дает эта решетка. Определить угол φ дифракции, соответствующий послед­нему максимуму.

31.18. При освещении дифракционной решетки белым светом спектры второго и третьего порядков отчасти перекрывают друг друга. На какую длину волны в спектре второго порядка наклады­вается фиолетовая граница (λ=0,4 мкм) спектра третьего порядка?

31.19. На дифракционную решетку, содержащую n =500 штри­хов на 1 мм, падает в направлении нормали к ее поверхности белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить ширину b спектра первого порядка на экране, если расстояние L линзы до экрана равно 3 м. Границы видимости спектра λ_кр=780 им, λ_Ф=400 нм.

31.20. На дифракционную решетку с периодом d =10 мкм под углом α=30° падает монохроматический свет с длиной волны λ=600 нм. Определить угол φ дифракции, соответствующий вто­рому главному максимуму.

31.21. Дифракционная картина получена с помощью дифрак­ционной решетки длиной l =1,5 см и периодом d =5 мкм. Определить, в спектре какого наименьшего порядка этой картины получатся раздельные изображения двух спектральных линий с разностью длин волн Δλ=0,1 нм, если линии лежат в крайней красной части спектра (λ 760 нм).

31.22. Какой наименьшей разрешающей силой R должна обла­дать дифракционная решетка, чтобы с ее помощью можно было раз­решить две спектральные линии калия (λ₁=578 нм и λ₂=580 нм)? Какое наименьшее число N штрихов должна иметь эта решетка, чтобы разрешение было возможно в спектре второго порядка?

31.23. С помощью дифракционной решетки с периодом d =20 мкм требуется разрешить дублет натрия (λ₁=589,0 нм и λ₂=589,6 нм) в спектре второго порядка. При какой наименьшей длине l решетки это возможно?

31.24. Угловая дисперсия D_φ дифракционной решетки для излу­чения некоторой длины волны (при малых углах дифракции) сос­тавляет 5 мин/нм. Определить разрешающую силу R этой решетки для излучения той же длины волны, если длина l решетки равна 2 см.

31.25. Определить угловую дисперсию Dφ дифракционной решет­ки для угла дифракции φ==30° и длины волны λ=600 нм. Ответ вы­разить в единицах СИ и в минутах на нанометр.

31.26. На дифракционную решетку, содержащую n =500 штри­хов на 1 мм, падает нормально монохроматический свет с длиной волны λ=700 нм. За решеткой помещена собирающая линза с глав­ным фокусным расстоянием f =50 см. В фокальной плоскости линзы расположен экран. Определить линейную дисперсию D_l такой сис­темы для максимума третьего порядка. Ответ выразить в милли­метрах на нанометр.

31.27. Нормально поверхности дифракционной решетки падает пучок света. За решеткой помещена собирающая линза с оптичес­кой силой Ф=1 дптр. В фокальной плоскости линзы расположен экран. Определить число п штрихов на 1 мм этой решетки, если при малых углах дифракции линейная дисперсия D_l =1 мм/нм.

31.28. На дифракционную решетку нормально ее поверхности падает монохроматический свет (λ=650 нм). За решеткой находится линза, в фокальной плоскости которой расположен экран. На экра­не наблюдается дифракционная картина под углом дифракции φ=30°. При каком главном фокусном расстоянии f линзы линейная дисперсия D_l =0,5 мм/нм?