Процесс принятия решений, касающихся инвестиций в инновационные проекты (выбор приемлемых и отклонение невыгодных проектов), называется составлением бюджета капиталовложений.
Оценка и выбор инвестиционных проектов предполагает последовательное прохождение 6 этапов:
1-ый этап: определение затрат, связанных с проектом.
2-ой этап: оценка ожидаемых чистых денежных потоков в каждом из последующих периодов.
3-ий этап: анализ риска чистых денежных потоков.
4-ый этап: определение на основе оценки риска чистых денежных потоков цены (стоимости) капитала.
5-ый этап: расчет текущей стоимости чистых денежных потоков.
6-ой этап: сравнение текущей стоимости ожидаемых чистых денежных потоков со стартовыми затратами по проекту (если данная стоимость превышает эти затраты, то проект следует, принять в противном случае – отклонить).
Основное отличие процесса принятия решения по инвестированию в долгосрочные проекты от инвестирования в текущую деятельность состоит в определении и сравнение доходов по капиталовложениям с доходами от равных по риску инвестиций в ценные бумаги или вложения денежных средств на депозитный счет в банк.
Дисконтирование денежных потоков – это метод оценки, который принимает в расчет изменения стоимости денег во времени.
ВАЖНО! Стоимость денег определяется не их обесценением в результате инфляции, а будущими доходами при их инвестировании (теория вмененных издержек или упущенной выгоды).
Все сложные методы оценки экономической эффективности инвестиций в инновационные проекты основываются на дисконтировании денежных потоков, так как, принимая решение о капиталовложениях, необходимо привести поступления и расходы денежных средств за разные годы к сопоставимым величинам. Будущие потоки денежных средств должны быть выражены через стоимость в текущем времени (сегодняшнюю покупательную способность, приведенную стоимость).
Основными сложными методами оценки экономической эффективности инвестиций являются:
1) ПРИВЕДЕННАЯ СТОИМОСТЬ (PV = PRESENT VALUE)
PV = S 
= S FV* 
, где
PV – приведенная стоимость (в текущем времени, сегодняшняя покупательная способность);
FV – будущая стоимость денег (будущие денежные потоки);
– коэффициент дисконтирования (r – ставка рефинансирования, t – число периодов).
ВАЖНО! Можно использовать табличные значения коэффициентов, но они несколько искажают результат за счет округления.
При равномерных будущих потоках денежных средств (аннуитет), приведенную стоимость можно рассчитать по формуле:
PV = An * KDIS, где
An – равномерные будущие потоки денежных средств;
KDIS – коэффициент дисконтирования аннуитета (табличное значение).
2) ЧИСТАЯ ПРИВЕДЕННАЯ СТОИМОСТЬ (NPV = NOT PRESENT VALUE)
NPV = PV – I0, где
NPV – чистая приведенная стоимость (чистый дисконтированный доход);
PV – приведенная стоимость (в текущем времени, сегодняшняя покупательная способность);
I0 – первоначальные инвестиции (инвестиции на нулевом этапе доходности проекта).
3) ИНДЕКС РЕНТАБЕЛЬНОСТИ (PI = PROFITABILITY INDEX)
PI =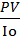 
, где
PI – индекс рентабельности;
PV – приведенная стоимость (в текущем времени, сегодняшняя покупательная способность);
I0 – первоначальные инвестиции (инвестиции на нулевом этапе доходности проекта).
4) ВНУТРЕННЯЯ НОРМА ПРИБЫЛИ (ДОХОДНОСТИ)
(IRR = INTERNAL RATE OF RETURN)
Внутренняя норма доходности представляет собой точную ставку процентов дохода от капиталовложений в течение срока инвестирования. Этот показатель иначе называют дисконтированной нормой прибыли.
Внутренняя норма доходности проекта свидетельствуют о его способности генерировать прибыль, то есть она должна быть выше стоимости капитала (инвестиций).
Внутреннюю норму доходности можно представить как ставку дисконтирования, при которой чистая приведенная стоимость будет равна нулю или приведенная стоимость поступлений равна стоимости первоначальных инвестиций.
Наиболее простым методом нахождения внутренней нормы доходности является метод интерполяции* (* Метод интерполяции – это оценка величины неизвестного числа, которые находятся где-то между двумя известными числами).
Для этого необходимо методом подбора получить два значения чистой приведенной стоимости (положительное и отрицательное), изменяя ставку дисконтирования, после чего, подставляя значения в формулу, можно будет найти значение ставки дисконтирования, при которой NPV=0.
IRR = rmin +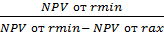 
(rmax – rmin), где
IRR – внутренняя норма доходности, т.е. ставка дисконтирования, при которой чистый доход (чистая приведенная стоимость) будет равно нулю;
rmin – минимальная ставка дисконтирования, выраженная в процентах (меньшая из двух, т.е. та, при которой NPV > 0;
rmax – максимальная ставка дисконтирования, выраженная в процентах (большая из двух, т.е. та, при которой NPV < 0;
NPV от rmin – чистая приведенная стоимость от минимальной ставки дисконтирования из двух рассматриваемых;
NPV от rmax – чистая приведенная стоимость от максимальной ставки дисконтирования из двух рассматриваемых.