Ответ 0.753
Задание номер 565.
Случайная величина распределена нормально с неизвестным среднеквадратичным отклонением. Полуширина δ доверительного интервала для оценки математического ожидания по выборочному среднему (объем выборки 25, «исправленное» выборочное среднеквадратичное отклонение 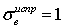 ) с надежностью 0,99 равна:
) с надежностью 0,99 равна:
Ответ 0.559
Задание номер 566.
Случайная величина распределена нормально со среднеквадратичным отклонением σ= 3. Оценка математического ожидания по выборочному среднему уложится в доверительный интервал с полушириной δ= 1 при объеме выборки 9 с вероятностью:
Ответ 0.68 или 68%
Задание номер 567.
Случайная величина распределена нормально со среднеквадратичным отклонением σ= 3. Чтобы обеспечить полуширину δ= 1 доверительного интервала для оценки математического ожидания по выборочному среднему с надежностью 0,999, необходимо использовать объем выборки не менее:
Ответ не менее 100
Задание номер 568.
Случайная величина распределена нормально со среднеквадратичным отклонением σ= 1. Полуширина δ доверительного интервала для оценки математического ожидания по выборочному среднему (объем выборки 25) с надежностью 0,95 равна:
Ответ 0.413
Задание номер 569.
Полуширина 90% доверительного интервала, построенного для оценки неизвестного математического ожидания нормально распределенной случайной величины X для объема выборки n=120, выборочного среднего 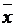 =23 и при неизвестной дисперсии с оценкой S=5, есть
=23 и при неизвестной дисперсии с оценкой S=5, есть
Ответ 0.753
Задание номер 570.
Случайная величина распределена нормально с неизвестным среднеквадратичным отклонением. Полуширина δ доверительного интервала для оценки математического ожидания по выборочному среднему (объем выборки 20, «исправленное» выборочное среднеквадратичное отклонение 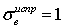 ) с надежностью 0,95 равна:
) с надежностью 0,95 равна:
Ответ 0.468
Задание номер 571.
Случайная величина распределена нормально со среднеквадратичным отклонением σ= 1. Оценка математического ожидания по выборочному среднему уложится в доверительный интервал с полушириной δ= 0,6 при объеме выборки 15 с вероятностью:
Ответ 0.98 или 98%
Задание номер 572.
Случайная величина распределена нормально со среднеквадратичным отклонением σ= 10. Чтобы обеспечить полуширину δ= 2 доверительного интервала для оценки математического ожидания по выборочному среднему с надежностью 0,9, необходимо использовать объем выборки не менее:
Ответ не менее 68
Задание номер 573.
Случайная величина распределена нормально с оценкой среднеквадратичного отклонения S= 4. Полуширина δ доверительного интервала для оценки математического ожидания по выборочному среднему (объем выборки 30) с надежностью 0,98 равна:
Ответ 1.798
Задание номер 574.
Полуширина 95% доверительного интервала, построенного для оценки неизвестного математического ожидания нормально распределенной случайной величины X для объема выборки n=100, выборочного среднего 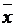 =23 и известного значения
=23 и известного значения 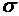 =4, есть
=4, есть
Ответ 0.784
Задание номер 575. Случайная величина распределена нормально с неизвестным среднеквадратичным отклонением. Полуширина δ доверительного интервала для оценки математического ожидания по выборочному среднему (объем выборки 40, «исправленное» выборочное среднеквадратичное отклонение 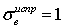 ) с надежностью 0,9 равна:
) с надежностью 0,9 равна:
Ответ 0.261
Задание номер 576. Случайная величина распределена нормально со среднеквадратичным отклонением σ= 10. Оценка математического ожидания по выборочному среднему уложится в доверительный интервал с полушириной δ= 3 при объеме выборки 25 с вероятностью:
Ответ 0.87 или 87%
Задание номер 577. Случайная величина распределена нормально со среднеквадратичным отклонением σ= 8. Чтобы обеспечить полуширину δ= 3 доверительного интервала для оценки математического ожидания по выборочному среднему с надежностью 0,999, необходимо использовать объем выборки не менее:
Ответ не менее 81
Задание номер 578. Случайная величина распределена нормально с оценкой среднеквадратичного отклонения S= 4. Полуширина δ доверительного интервала для оценки математического ожидания по выборочному среднему (объем выборки 20) с надежностью 0,95 равна:
Ответ 1.872
Задание номер 579. Полуширина 80% доверительного интервала, построенного для оценки неизвестного математического ожидания нормально распределенной случайной величины X для объема выборки n=80, выборочного среднего 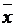 =23 и известного значения
=23 и известного значения 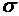 =5, есть
=5, есть
Ответ 0.721
Задание номер 580. Случайная величина распределена нормально с неизвестным среднеквадратичным отклонением. Полуширина δ доверительного интервала для оценки математического ожидания по выборочному среднему (объем выборки 50, «исправленное» выборочное среднеквадратичное отклонение 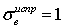 ) с надежностью 0,9 равна:
) с надежностью 0,9 равна:
Ответ 0.233
Задание номер 581. Случайная величина распределена нормально со среднеквадратичным отклонением σ= 2. Оценка математического ожидания по выборочному среднему уложится в доверительный интервал с полушириной δ= 0,5 при объеме выборки 16 с вероятностью:
Ответ 0.68 или 68%
Задание номер 582. Случайная величина распределена нормально со среднеквадратичным отклонением σ= 1. Чтобы обеспечить полуширину δ= 0,5 доверительного интервала для оценки математического ожидания по выборочному среднему с надежностью 0,99, необходимо использовать объем выборки не менее:
Ответ не менее 27
Задание номер 583. Случайная величина распределена нормально с оценкой среднеквадратичного отклонения S= 6. Полуширина δ доверительного интервала для оценки математического ожидания по выборочному среднему (объем выборки 16) с надежностью 0,99 равна:
Ответ 4.421
Задание номер 584. Найти доверительный интервал для оценки с надежностью  неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, если известны выборочная средняя
неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, если известны выборочная средняя  ,генеральное среднеквадратическое отклонение
,генеральное среднеквадратическое отклонение 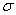 и объём выборки n (
и объём выборки n (  =10,2;
=10,2; 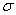 =4; n = 16;
=4; n = 16;  = 0,99)
= 0,99)
Ответ 7.25 < m < 13.15
Задание номер 585. По выборке из 25 упаковок товара средний вес составил 101 г с исправленным средним квадратическим отклонением 3 г. Построить доверительный интервал для среднего с вероятностью 90 %. Предполагается, что вес – это нормально распределенная случайная величина.
Ответ 5.9341 < 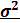 <15.6522
<15.6522
Задание номер 586. Импортер упаковывает чай в пакеты. Известно, что наполняющая машина работает со стандартным отклонением  . Выборка 50 пакетов показала средний вес 125,8. Найти доверительный интервал для среднего веса в генеральной совокупности с вероятностью 95 %. Генеральная совокупность распределена нормально.
. Выборка 50 пакетов показала средний вес 125,8. Найти доверительный интервал для среднего веса в генеральной совокупности с вероятностью 95 %. Генеральная совокупность распределена нормально.
Ответ 125.73 < 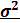 < 131.27
< 131.27
Задание номер 587. По выборке из 25 упаковок товара средний вес составил 101 г с исправленным средним квадратическим отклонением 3 г. Построить доверительный интервал для дисперсии с вероятностью 90 %. Предполагается, что вес – это нормально распределенная случайная величина.
Ответ 5.9341 < 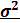 <15.6522
<15.6522
Задание номер 588. По данным выборки объема 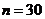 из генеральной совокупности нормально распределенного количественного признака найдено среднее квадратическое отклонение
из генеральной совокупности нормально распределенного количественного признака найдено среднее квадратическое отклонение 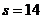 . Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение
. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение 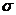 с надежностью
с надежностью 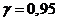 .
.
Ответ 10.08 <σ <17.92
Задание номер 589. Для отрасли составлена случайная выборка из 19 фирм. По выборке оказалось, что в фирме в среднем работают 77,5 человека при среднем квадратическом отклонении 25 человек. Пользуясь 95 % доверительным интервалом, оценить среднее число работающих в фирме по всей отрасли. Предполагается, что количество работников фирмы имеет нормальное распределение.
Ответ 1134.5 < m <1289.5
Тема 1.1 Случайные события
Задание номер 01. Условной вероятностью события A при условии события B называется
называется вероятность события A, вычис-
ленная в предположении, что событие B уже произошло. 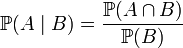 (P.S. P(AnB)=P(AB))
(P.S. P(AnB)=P(AB))
Задание номер 02. Ниже приведены четыре формулы. Какие из них верны, если А и В – некоторые события и 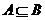 ?
?
???
Задание номер 03. Какое условие необходимо, чтобы была определена условная вероятность события А при условии В Р(А/В)?
Р(В) > 0
Задание номер 04. Укажите, какое равенство есть определение независимых событий. События А и В независимы, если
P(AB) = P(A)*P(B).
Задание номер 05. Условной вероятностью 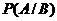 называют:
называют:
называется вероятность события A, вычисленная в предположении, что событие B уже произошло.
Задание номер 06. Выберите формулу Байеса
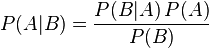
Задание номер 07. Выберите формулу полной вероятности
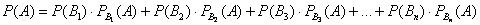
Задание номер 08. Формула полной вероятности определяет
Вероятность события А, которое может наступить при условии по-
явления одного из несовместных событий B1, B2,..., Bn, образующих полную
группу и называемых гипотезами, равна сумме произведений вероятностей
каждого из этих событий на соответствующую условную вероятность события
Задание номер 09. Условной вероятностью события A при условии события B называется
называется вероятность события A, вычис-
ленная в предположении, что событие B уже произошло. 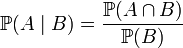 (P.S. P(AnB)=P(AB))
(P.S. P(AnB)=P(AB))
Задание номер 10. Укажите, какое равенство есть определение независимых событий. События А и В независимы, если
P(AB) = P(A)*P(B).
Задание номер 11. Условной вероятностью 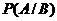 называют:
называют:
называется вероятность события A, вычисленная в предположении, что событие B уже произошло.
Задание номер 12. Одной из аксиом теории вероятностей является утверждение:
Аксиома 1. Каждому случайному событию A соответствует определенное число Р(А), называемое его вероятностью и удовлетворяющее условию.
Аксиома 2. Вероятность достоверного события равна единице.
Аксиома 3 (аксиома сложения вероятностей). Пусть A и В — несовместные события. Тогда вероятность того, что произойдет хотя бы одно из этих двух событий, равна сумме их вероятностей:
P(A+B)=P(A)+P(B)
Задание номер 13. Количество аксиом теории вероятностей равно:
Задание номер 14-15. Одним из следствий аксиом теории вероятностей является утверждение:
1. Вероятность невозможного события равна нулю: P(∅) = 0.
2. Для любого события А P(A¯)=1−P(A).
3. Каково бы ни было случайное событие А, 0 ≤ P(A) ≤ 1.
4. Если событие А влечет за собой событие В, то P(A) ≤ P(B).
5. P(A+ B) = P(A) + P(B) - P(AB).
6. P(A + B) <= P(A) + P(B).
Задание номер 16. Одной из аксиом теории вероятностей является утверждение:
Аксиома 1. Каждому случайному событию A соответствует определенное число Р(А), называемое его вероятностью и удовлетворяющее условию.
Аксиома 2. Вероятность достоверного события равна единице.
Аксиома 3 (аксиома сложения вероятностей). Пусть A и В — несовместные события. Тогда вероятность того, что произойдет хотя бы одно из этих двух событий, равна сумме их вероятностей:
P(A+B)=P(A)+P(B)
Задание номер 17-18. Событие B называется независимым от события А, если:
если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности:
Р(В|A) = Р (В).
Задание номер 19. Если события 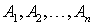 не являются независимыми в совокупности, то справедливы соотношения:
не являются независимыми в совокупности, то справедливы соотношения:
???
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.
Задание номер 20. Формулы Байеса гласят:
гласит, что вероятность наступления «события» при условии проведения «наблюдения» равна произведению вероятности наступления события и вероятности проведения наблюдения при условии наступления события, деленному на безусловную вероятность проведения наблюдения
Задание номер 21. Формула полной вероятности гласит:
Если событие А может произойти только при выполнении одного из событий 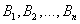 , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
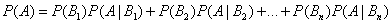
Задание номер 22. Какое максимальное количество гипотез в формуле полной вероятности можно взять?
???Не ограничено
Задание номер 23. В формуле полной вероятности 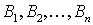 — гипотезы. Каким из перечисленных свойств они удовлетворяют?
— гипотезы. Каким из перечисленных свойств они удовлетворяют?
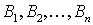 несовместные события
несовместные события
Задание номер 24. Формулы Байеса определяют:
вероятность наступления «события» при условии проведения «наблюдения»
Задание номер 25. Формула полной вероятности определяет:
Вероятность события А, при условии что А может наступить лишь про появлении одного из несовместных событий B1,B2…Bn
Задание номер 26. Соотношение  , где Bj — гипотезы, называется:
, где Bj — гипотезы, называется:
Формула полной вероятности
Задание номер 27. Пусть 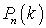 — формула Бернулли, где n — число испытаний, k — число удач. Какова вероятность, что в серии из n испытаний будет не менее, чем m удач?
— формула Бернулли, где n — число испытаний, k — число удач. Какова вероятность, что в серии из n испытаний будет не менее, чем m удач?
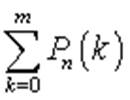
Задание номер 28. Формула Лапласа определяет:
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p
(0 < p < 1), событие наступит ровно k раз (безразлично, в какой последова-
тельности)
Задание номер 29. Использование формулы Лапласа оправдано при:
большом значении n
Задание номер 30. Преимущество использования приближенной формулы Лапласа вместо точной формулы Бернулли состоит в том, что:
Не такие громоздкие вычисления
Задание номер 31. Формула Лапласа гласит:
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p
(0 < p < 1), событие наступит ровно k раз (безразлично, в какой последовательности)
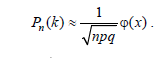
Задание номер 32. Преимущество использования приближенной формулы Пуассона вместо точной формулы Бернулли состоит в том, что:
Не такие громоздкие вычисления
Задание номер 33. Формула Пуассона определяет:
вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз
Задание номер 34. Формула Пуассона гласит:
вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k
раз, приближенно равна

Задание номер 35. Формулой Бернулли называется формула:

Задание номер 36. Если вероятность наступления события A в каждом испытании равна 0,25, то для нахождения вероятности того, что событие A наступит от 215 до 300 раз в 1000 испытаниях, вы воспользуетесь:
Формулой Лапласа
Задание номер 37. Если вероятность наступления события A в каждом испытании равна 0,002, то для нахождения вероятности того, что событие A наступит 3 раза в 1000 испытаниях, вы воспользуетесь:
Формулой Пуассона
Задание номер 38. Из какого неравенства определяется наивероятнейшее число m0 наступления события в n независимых испытаниях, в каждом из которых вероятность появления события равна Р?
np – p <m0 < np + p,
Задание номер 39. В группе 7 юношей и 5 девушек. На конференцию выбирают трех студентов случайным образом (без возвращения). Определить вероятность того, что на конференцию поедут двое юношей и одна девушка.
21/44
Задание номер 40. В корзине содержится 6 черных и 5 белых шаров. Случайным образом вынимают 5 шаров. Найти вероятность того, что среди них имеется 3 белых шара
25/77
Задание номер 41. Из урны содержащей, 6 белых шаров, 5 черных и 3 красных, достают наугад 4 шара. Найти вероятность, что среди вынутых шаров есть хотя бы по одному шару каждого цвета
990/1001
Задание номер 42. Из шести букв разрезной азбуки составлено слово «ананас». Ребенок, не умеющий читать, рассыпал эти буквы и затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово «ананас».
1/120
Задание номер 43. Из шести букв разрезной азбуки составлено слово «книга». Ребенок, не умеющий читать, рассыпал эти буквы и затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово «книга».
1/120
Задание номер 44. Из полного набора костей домино (28 костей) наудачу берутся пять костей. Найти вероятность того, что среди них будет хотя бы одна с шестеркой.
0,793
Задание номер 45. Имеются пять билетов стоимостью по одному рублю, три билета по три рубля и два билета по пять рублей. Наугад берутся три билета. Определить вероятность того, что хотя бы два из этих билетов имеют одинаковую стоимость.
3/4
Задание номер 46. Имеются пять билетов стоимостью по одному рублю, три билета по три рубля и два билета по пять рублей. Наугад берутся три билета. Определить вероятность того, что все три билета стоят семь рублей.
7/24
Задание номер 47. В пачке 20 перфокарт, помеченных номерами 101, 102,..., 120 и произвольно расположенных. Перфораторщица наудачу извлекает две карты. Найти вероятность того, что извлечены перфокарты с номерами 101 и 120.
1/190
Задание номер 48. В ящике 10 одинаковых деталей, помеченных 1,2,…,10. Наудачу извлечены 6 деталей. Найти вероятность того, что среди извлеченных деталей окажется деталь № 1
0,6
Задание номер 49. В ящике 10 одинаковых деталей, помеченных 1,2,…,10. Наудачу извлечены 6 деталей. Найти вероятность того, что среди извлеченных деталей окажутся детали № 1 и № 2
1/3
Задание номер 50. В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.
0,2
Задание номер 51. В группе 7 юношей и 5 девушек. На конференцию выбирают трех студентов случайным образом (без возвращения). Определить вероятность того, что на конференцию поедут двое юношей и одна девушка.
21/44
Задание номер 52. Игральную кость бросают 5 раз. Вероятность того, что ровно 3 раза появится нечетная грань, равна:
5/16
Задание номер 53. Числа 1, 2, 3, 4, 5 написаны на пяти карточках. Наугад последовательно выбираются три карточки, и вынутые таким образом цифры ставятся слева направо. Вероятность того, что полученное при этом трехзначное число будет четным равна:
2/5
Задание номер 54. В партии из 50 деталей 5 нестандартных. Определить вероятность того, что среди выбранных наудачу для проверки 6 деталей 2 окажутся нестандартными.
0,08
Задание номер 55. На 10 карточках написаны буквы: A, А, А, А, А, Р, Р, Р, Д, Д. Наугад берется 5 карточек и прикладывается одна к другой слева направо. Какова вероятность того, что случайно будет сложено слово РАДАР?
0,00794
Задание номер 56. Брошены три игральные кости. Найти вероятность следующих событий: A = {на всех костях выпало по 5 очков}, B = {на всех костях выпало одно и то же число очков.}
1/216; 1/36
Задание номер 57. В ящике лежат 12 красных, 8 зеленых, 10 синих шаров. Наудачу вынимается два шара. Найти вероятность того, что будут вынуты шары разного цвета.
0,320
Задание номер 58. На 10 карточках написаны буквы: А, А, А, А, А, А, М, М, М, М. Ребенок наугад вытаскивает одну за другой 4 карточки и прикладывает их друг к другу слева направо. Какова вероятность того, что он случайно сложит слово МАМА?
0,0714
Задание номер 59. Слово МАТЕМАТИКА разрезается на буквы. Буквы перемешиваются и снова складываются слева направо. Найти вероятность того, что снова получится слово МАТЕМАТИКА.
6,2×10-5
Задание номер 60. Покупателю предлагается 50 лотерейных билетов, из которых 4 выигрышных. Покупатель покупает наугад три билета. Найти вероятность события: A = {куплены все выигрышные билеты}.
0,0002
Задание номер 61. Студент знает 14 вопросов программы из 20. В билете содержится 3 вопроса. Вероятность того, что студент ответит не менее чем на два вопроса из трех
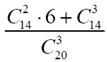
Задание номер 62. Из колоды, содержащей 36 карт, достают наугад три карты. Вероятность того, что среди них будет не более одного туза
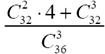
Задание номер 63. В денежно-вещевой лотерее на серию в 100 билетов приходится 12 денежных и 8 вещевых выигрышей. Вероятность того, что из трех купленных билетов хотя бы два окажутся выигрышным
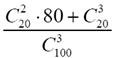
Задание номер 64. В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц окажутся все женщины.
l/6
Задание номер 65. В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц окажутся все мужчины.
l/30
Задание номер 66. Из колоды в 52 карты наугад выбираются 4. Найти вероятность того, что среди них окажется один туз.
0,2556
Задание номер 67. На стеллаж случайным образом расставлены 15 книг, причем 6 из них в переплете. Определить вероятность того, что из трех взятых наугад книг хотя бы одна будет в переплете.
53/65
Задание номер 68. На 10 карточках написаны цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Две карточки вынимаются и укладываются в порядке появления. Найти вероятность того, что получившееся двузначное число — нечетное.
1/2
Задание номер 69. В магазине имеется 14 телевизоров. Из них 10 — импортных. Найти вероятность того, что среди 6 наудачу взятых телевизоров 4 импортных.
60/143
Задание номер 70. В магазине имеется 14 телевизоров. Из них 10 — импортных. Найти вероятность того, что среди 6 наудачу взятых телевизоров все телевизоры импортные.
10/143
Задание номер 71. Число дополнительных вопросов, задаваемых на экзамене, равно 25. Из них 10 - по теории вероятностей, а остальные — по другим разделам математики. Студенту задано 3 вопроса. Найти вероятность того, что два из них по теории вероятностей.
27/92
Задание номер 72. Число дополнительных вопросов, задаваемых на экзамене, равно 25. Из них 10 - по теории вероятностей, а остальные — по другим разделам математики. Студенту задано 3 вопроса. Найти вероятность того, что все три вопроса по теории вероятностей.
6/115
Задание номер 73. Некто забыл номер нужного ему телефона. Помня только, что все 5 цифр номера различные, набрал номер наудачу. Найти вероятность того, что номер набран правильно.
4*10-5
Задание номер 74. В коробке 6 одинаковых пронумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера кубиков появятся в возрастающем порядке.
1/720
Задание номер 75. В группе из 25 студентов, среди которых 10 девушек, разыгрываются 5 билетов. Найти вероятность того, что среди обладателей билетов окажется две девушки;
0.385
Задание номер 76. В группе из 25 студентов, среди которых 10 девушек, разыгрываются 5 билетов. Найти вероятность того, что среди обладателей билетов окажется не более двух девушек.
0.6988
Задание номер 77. На карточках написаны буквы: «ааедкнт». Чему равна вероятность сложить с первого раза слово «деканат»
0.0004
Задание номер 78. На карточках написаны буквы: «ееннижр». Чему равна вероятность сложить с первого раза слово «инженер»?
0.0008
Задание номер 79. Среди кандидатов в сборную университета по волейболу 3 первокурсника, 5 второкурсников и 7 третьекурсников. Из этого состава наудачу выбирают 5 человек. Какова вероятность того, что в состав команды будет выбран один первокурсник?
1/143
Задание номер 80. Среди кандидатов в сборную университета по волейболу 3 первокурсника, 5 второкурсников и 7 третьекурсников. Из этого состава наудачу выбирают 5 человек. Какова вероятность того, что в состав команды будут выбраны два второкурсника и два третьекурсника?
70/143
Задание номер 81. На семи карточках написаны буквы: «а, а, н, н, н, т, е». После тщательного перемешивания 7 раз наугад вынимают по одной карточке с последующим их возвращением. Каждая буква на карточке записывается. Найти вероятность того, что в результате будет записано слово «антенна».
0.00238
Задание номер 82. Телефонный номер состоит из 6 цифр. Найти вероятность того, что среди них две цифры одинаковые.
0.4536
Задание номер 83. У сборщика 12 деталей, мало отличающихся друг от друга. Из них 5 — одного вида, 4 — второго вида, 3 — третьего вида. Какова вероятность того, что среди шести взятых наугад деталей окажется 3 — первого вида, 2 — второго вида и 1 — третьего вида.
15/77
Задание номер 84. Устройство состоит из 5 элементов, из которых 2 элемента изношены. При включении устройства случайным образом включаются 2 элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.
0.3
Задание номер 85. Устройство состоит из 5 элементов, из которых 2 элемента изношены. При включении устройства случайным образом включаются 2 элемента. Найти вероятность того, что включенными окажутся изношенные элементы.
0.1
Задание номер 86. На тепловой электростанции работает 15 сменных инженеров, из них 4 женщины. В смене занято 4 человека. Найти вероятность того, что в случайно выбранную смену войдут не менее двух мужчин.
0.967
Задание номер 87. Телефонный номер состоит из 6 цифр. Найти вероятность того, что все цифры различные.
0.1512
Задание номер 88. Наблюдениями установлено, что в мае в среднем бывает 16 дождливых дней. Какова вероятность, из случайно взятых в этом месяце семи дней четыре окажутся солнечными?
0.29
Задание номер 221. Найти коэффициент корреляции.

-0,1
Задание номер 222. Найти коэффициент корреляции.

-0,08
Задание номер 223. Найти коэффициент корреляции.

-0,04
Задание номер 224. Найти коэффициент корреляции.

0,05
Задание номер 225. Найти коэффициент корреляции.

-0,18
Задание номер 226. Найти коэффициент корреляции.

0,02
Задание номер 227. Найти коэффициент корреляции.

-0,14
Задание номер 228. Найти коэффициент корреляции.

-0,32
Задание номер 229. Найти коэффициент корреляции.

-0,07
Задание номер 230. Найти коэффициент корреляции.

-0,09
Задание номер 231. Найти коэффициент корреляции.

-0,23
Задание номер 232. Найти коэффициент корреляции.

-0,13
Задание номер 233. Найти коэффициент корреляции.

0,006
Задание номер 234. Найти коэффициент корреляции.

-0,01
Задание номер 235. Найти коэффициент корреляции.

-0,06
Задание номер 236. Найти коэффициент корреляции.

-0,04
Задание номер 237. Найти коэффициент корреляции.

-0,17
Задание номер 238. Найти коэффициент корреляции.

-0,06
Задание номер 239. Найти коэффициент корреляции.

-0,12
Задание номер 240. Найти коэффициент корреляции.

-0,09
Задание номер 241. Найти коэффициент корреляции.

-0,16
Задание номер 242. Найти коэффициент корреляции.

0,03
Задание номер 243. Найти коэффициент корреляции.

0,07
Задание номер 244. Найти коэффициент корреляции.

-0,01
Задание номер 245. Найти коэффициент корреляции.

-0,03
Задание номер 246. Найти коэффициент корреляции.

0,03
Задание номер 247. Найти коэффициент корреляции.

-0,24
Задание номер 248. Найти коэффициент корреляции.

-0,04
Задание номер 249. Найти коэффициент корреляции.

0,01
Задание номер 250. Найти коэффициент корреляции.

-0,12
Задание номер 251. Найти коэффициент корреляции.

-0,03
Задание номер 252. Найти коэффициент корреляции.

0,04
Задание номер 253. Найти коэффициент корреляции.

-0,03
Задание номер 254. Найти коэффициент корреляции.

0,03
Задание номер 255. Найти коэффициент корреляции.

-0,02
Задание номер 256. Найти коэффициент корреляции.

-0,04
Задание номер 257. Найти коэффициент корреляции.

-0,01
Задание номер 258. Найти коэффициент корреляции.

-0,06
Задание номер 259. Найти коэффициент корреляции.

-0,02
Задание номер 260. Найти коэффициент корреляции.

-0,04
Задание номер 261. Найти коэффициент корреляции.

под корнем получается отрицательное число
Задание номер 262. Найти коэффициент корреляции.

-1
Задание номер 263. Найти коэффициент корреляции.

-0,15
Задание номер 264. Найти коэффициент корреляции.

0,02
Задание номер 265. Найти коэффициент корреляции.

-0,14
Задание номер 266. Найти коэффициент корреляции.

0,01
Задание номер 267. Найти коэффициент корреляции.

нет числа
Задание номер 268. Найти коэффициент корреляции.

-0,09
Задание номер 269. Найти коэффициент корреляции.

-0,04
Задание номер 270. Найти коэффициент корреляции.

-0,05
Задание номер 271. Найти коэффициент корреляции.

0,1
Задание номер 145. График плотности распределения случайной величины имеет вид
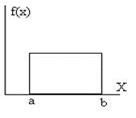
Какому закону распределения соответствует график?
Равномерное
Задание номер 146. –
Задание номер 147. Производится 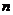 независимых испытаний, в каждом из которых событие А может появится с вероятностью
независимых испытаний, в каждом из которых событие А может появится с вероятностью 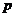 или не появиться с вероятностью
или не появиться с вероятностью  . По какому закону распределена случайная величина: m- количество появлений события А в
. По какому закону распределена случайная величина: m- количество появлений события А в 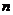 опытах? Биноминальное
опытах? Биноминальное
Задание номер 148. График плотности распределения случайной величины имеет вид 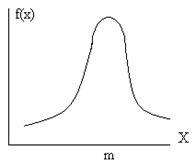 График плотности распред
График плотности распред