
Скорость изнашивания, млг/мин
Рисунок 43. Пример простой полосовой диаграммы
Простая полосовая диаграмма употребляется для сравнения двух или нескольких сравниваемых величин. Сравнение делается на основании прямых линейных измерений. Полосы обычно располагаются в последовательности, соответствующей относительной величине показателей.
Расположение полос на простой полосовой (или линейчатой) диаграмме должно отвечать целям исследования. Обычно полосы располагают по величине, начиная с самой большой, но они могут быть расположены и в ином систематизированном порядке, если это отвечает цели составления диаграммы.
Ширина полос и расстояние между ними не имеют особого значения. Определяющим фактором при конструировании, как ширины полос, так и промежутков между ними, служит число полос, а также размер и пропорции всей диаграммы. Практически следует придерживаться правила: ширина полос на диаграмме должна быть одинаковой, а ширина промежутков - равна половине ширины самих полос. Не рекомендуется делать полосы непропорционально длинными и узкими или же короткими и широкими Важно, чтобы в каждую полосовую диаграмму включалась тщательно продуманная шкала - она и дает возможность с достаточной точностью определять длину полосы. Шкала может совпадать с верхней гранью первой полосы или же располагаться на отдельной линии в верхней части диаграммы. В этом случае промежуток между верхней полосой и линией шкалы должен быть равен половине ширины полосы.
Нулевая линия служит основной исходной точкой, и на рисунке ее следует изображать несколько толще, чем другие масштабные отметки на шкале. Желательно, чтобы шкала не прерывалась.
Оставлять контурные полосы неокрашенными не рекомендуется. Графически полосы выполняют, применяя текстуру и цвет.
При необходимости поместить на диаграмме данные не следует вписывать цифры внутри самих полос, а также на правом конце полосы. Если цифры проставляют непосредственно на самой полосе, то возникает тенденция сравнивать не всю длину полос, а только те их части, где нет цифр. Если же цифры вписывают справа от конца полосы, то создается впечатление, что полосы удлинены за счет цифр. Однако когда по каким-либо причинам все же приходится делать надписи на самих полосах, буквы должны быть небольшими и со всех сторон окруженными свободным пространством. Надписи у конца полосы тоже не должны быть крупными, их непременно надо отделить от полосы свободным промежутком. Основные данные, как правило, помещаются слева от нуля, за пределами полосы.
Полосовая с подразделениями диаграмма строится на основании абсолютных величин и на процентных числах. При помощи диаграммы такого типа можно не только графически изображать состав каких-либо совокупностей, но и сравнивать между собой различные их части. Технически такие диаграммы строятся, так же, как и простые полосовые, отличие заключается в том, что каждая полоса подразделяется на компоненты (см. рисунок 44).
Если значения данных, использованных в диаграмме, выражены в процентах, то применяется процентная шкала, т. е. все участки каждой полосы изображаются в их отношении к 100 %. Основная цель такой диаграммы - сравнение составных частей определенной совокупности в их процентном отношении к целому.
Отрезки полос в такой диаграмме должны быть расположены в их логической или аналитической последовательности, общепринятым является расположение по величине в убывающем порядке. Для графического выделения отдельных отрезков используются цвет и текстура. Если при этом применяется несколько способов штриховки, то обычно требуется экспликация к ним. Экспликация состоит из нескольких по-разному заштрихованных квадратов с кратким пояснением значения каждого вида штриховки. Если нет особых причин поступать иначе, то штриховку следует располагать по степени ее густоты, причем слева делается наиболее густая штриховка.
Различные компоненты целого могут быть также представлены в виде отдельных полос в ступенчатой форме. Самый большой отрезок обычно изображается сверху, а остальные располагаются ниже в зависимости от их величины. Категории «разные» и «прочие» помещают обычно снизу, хотя эти величины могут быть больше других составных частей (рисунок 45).
Относительный состав материалов
 Относительный состав материалов
Рисунок 44. Пример полосовой диаграммы
с подразделениями
Относительный состав материалов
Рисунок 44. Пример полосовой диаграммы
с подразделениями
| Время загрузки детали в приспособление
промышленными роботами
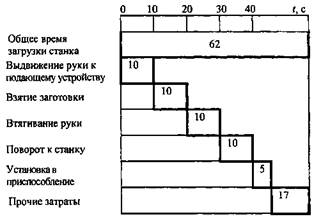 Рисунок 45. Пример ступенчатой полосовой диаграммы
Рисунок 45. Пример ступенчатой полосовой диаграммы
|
Парные, направленные и скользящие полосовые диаграммы представляют собой различные формы двухсторонних полосовых диаграмм. На диаграммах этого типа полосы вытягиваются вправо и влево от вертикальной линии деления. Двухсторонние полосовые диаграммы очень удобны для изображения положительных и отрицательных величин, приростов и уменьшений, а также для сравнения двух контрастных показателей.
Круговая диаграмма
Круговая диаграмма представляет собой круг, разделенный на секторы. Площади (или центральные углы) секторов пропорциональны изображенным значениям величин. Обычно такие диаграммы применяются для показа удельного веса составных частей целого: различные секторы круга как раз и демонстрируют составные части, или компоненты, целого (рисунок 46).
Общепринято для изображения соотношения составных частей применять одну из трех диаграмм: круговую, полосовую с процентными делениями либо простую полосовую. Каждая из этих трех графических моделей имеет свои преимущества. При выборе формы диаграммы необходимо учитывать такие факторы, как аудитория, для которой предназначается показ материала, и целевое назначение диаграммы. Более того, не существует подробных, точных, систематических и надежных тестов для сравнительной оценки различных видов диаграмм и графиков. Сравнительные оценки основаны, как правило, только на впечатлениях.
Структура затрат на производство продукции в промышленности за 1995 г., %

Рисунок 46. Пример круговой диаграммы
Для простых сравнений числовых данных, особенно, если имеется более четырех-пяти элементов, применяют полосовую диаграмму. При построении круговой диаграммы, прежде всего, необходимо так обработать данные, чтобы величины отдельных компонентов могли быть выражены в градусах окружности. Секторы на круговой диаграмме рекомендуется размещать в определенной логической последовательности. Чаще всего за основу берется их величина, причем самый крупный размещается сверху, а остальные - по движению часовой стрелки.
При акцентированном делении один из секторов выделяется размером, окраской или физическим отделением от целого, тем самым подчеркивается особое значение элемента.
Неопределенное деление используется для показа пределов возможного изменения делящих линий.
Сложное деление предполагает при помощи наложения секторов описывать области, принадлежащие по своему смыслу одновременно нескольким элементам. Дифференциация форм существенна, поскольку каждый из накладывающихся секторов должен четко опознаваться для передачи сложного деления.
Прочие диаграммы
Треугольная диаграмма применяется для одновременного изображения трех переменных, представляющих элементы, или составные части, целого. В сумме эти три величины всегда дают 100 %. Треугольная диаграмма состоит из трех шкал, построенных в виде равностороннего треугольника, каждая сторона которого разбивается на равные процентные деления от 0 до 100.
Параллельно сторонам треугольника проводят прямые линии. Треугольная диаграмма основана на геометрическом принципе, согласно которому для равностороннего треугольника сумма перпендикуляров, опущенных из любой точки прямоугольника на его стороны, есть величина постоянная и равная высоте треугольника. Ряд чисел, образующих шкалы, можно располагать последовательно как по часовой стрелке, так и против нее. Треугольная диаграмма полезна для изображения свойства химических соединений или сплавов, состоящих из трех элементов, операций, произведенных процессов (рисунок 47).
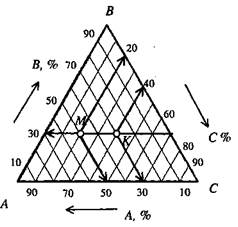
Рисунок 47. Диаграмма тройного сплава
Данная диаграмма состоит из трех шкал, построенных в виде треугольника. На каждой шкале откладывается величина одного из компонентов А, В, С в %. Любая точка, лежащая внутри треугольника, соответствует составу тройного сплава. За 100 % массы удобнее всего принять длину стороны треугольника, тогда масса компонентов в тройном сплаве определится отрезками, параллельными сторонам треугольника. В вершинах треугольника лежат точки, соответствующие чистым компонентам. В данном примере в сплаве М содержится, в %: компонента А - 50, В - 30, С - 20; в сплаве К содержится: компонента А - 30, В - 30, С-40.
Треугольная диаграмма не имеет шкалы времени, но на один треугольник можно наносить три-четыре показателя за разные периоды, обозначив точки соответствующими надписями (во избежание путаницы не следует наносить слишком много цифр).
Комбинированная диаграмма - отражает зависимости при помощи линий, геометрических фигур и рисунка на одном координатном поле.
Диаграмма состояния (диаграмма состав-свойство и др.) - графическое изображение зависимости между параметрами состояния системы либо между ними и составом системы и т. п. Под материальной системой в данном случае понимается некоторая часть пространства, заполненная веществом. Остальное окружающее пространство называется внешней средой. Материальная система может состоять из нескольких частей. Если эти части обмениваются энергией, то такую систему называют термодинамической; если возможен обмен не только энергией, но и веществом, то это физико-химическая система. В металловедении физико-химическими системами являются чистые металлы и их сплавы, т. е. простые и сложные по составу вещества, в которых при изменении внешних условий (температуры и давления) могут протекать различные превращения (например, плавление, переход из одной кристаллической формы в другую и пр.). Металлические сплавы образуют не только металлы, но и металлы с неметаллами. Графически состояния таких систем отображают с помощью диаграмм состояния: это графическое изображение фазового состояния сплавов данной системы в функциях температура и концентрация.
Диаграммы состояния, как правило, строят экспериментально, но существуют и теоретические методы их расчета по термодинамическим функциям с применением ЭВМ. Для экспериментального построения диаграммы состояния сплавов с несколькими компонентами необходимо изготовить серию сплавов, содержащих различные их количества. Для каждого такого сплава экспериментально строят кривые охлаждения и определяют по ним критические точки, т. е. температуры фазовых превращений. Полученные значения критических точек изучаемых сплавов откладывают на вертикальных линиях, соответствующих химическому составу этих сплавов. Затем соединяют критические точки, соответствующие определенным фазовым превращениям, и получают линии диаграммы состояний - это геометрическое место всех верхних точек, которые определяют температуры начала кристаллизации сплавов, называется линией ликвидус.
Трехмерная диаграмма отражает одновременное влияние двух факторов на исследуемый параметр. Правила построения ее аналогичны правилам построения двухмерной диаграммы. Необходимо отметить, что значительная часть трехмерных диаграмм имеет искажения и может давать неправильное представление о предмете исследования. При выполнении трехмерных диаграмм используют аксонометрические (прямоугольные и косоугольные) проекции и перспективу, причем применение перспективы в этом случае нужно обосновать.
Трехмерные диаграммы рекомендуют применять при составлении организационных диаграмм.
Объемной называется диаграмма, в которой сравниваемые количества выражены объемными изображениями (шары, конусы и пр.).
Номограммы
Номограмма - чертеж, с помощью которого можно, не производя вычислений, получать решения вычислительных задач. Говоря современным языком, номограмма - это жесткая программа графического способа решения задачи. Методы и процедуры построения номограмм составляют номографию как науку. Статус самостоятельного раздела математики номография приобрела на первом Международном конгрессе математиков в 1896 г. Задачи номографии - представление физических или математических законов в графической форме, в форме номограмм.
Номограмма моделирует функциональную зависимость, и ее можно использовать как доступное и удобное вычислительное средство и как весьма наглядное и эффективное средство исследования функциональных зависимостей. Номограммы позволяют проследить влияние отдельных переменных на результат, исследовать экспериментальные особенности функции, увидеть область существования решения, обнаружить ранее неизвестные свойства функциональных зависимостей.
Номограммы - полезное дополнение к ЭВМ. Если некая задача допускает номографическое решение, точность которого достаточна, то оно оказывается более эффективным, чем машинное решение этой же задачи, состоящее в разработке стандартной программы или расчете таблицы с несколькими входами. В том же случае, когда для данной задачи точность номограмм мала, их можно применять для прикидочных расчетов, для определения нулевых приближений, для контроля вычислений с целью обнаружения грубых ошибок. Выгодно совместное использование номограмм и ЭВМ при решении многопараметрических задач, когда результаты расчета представляются номограммами.

Рисунок 48. Пример номограммы с линейными
шкалами: d - диаметр заклепки; s - толщина скрепляемых деталей

Рисунок 49. Пример номограммы сетчатой
Номографические методы исследования функциональных зависимостей полезно применять в задачах подбора параметров эмпирических формул по результатам наблюдений и в задачах аппроксимации одной функции другой. Номограммы позволяют охватить взглядом все множество решений данной задачи и выбрать оптимальное, компактно и наглядно изображать таблицы с несколькими входами, исследовать положенные в их основу зависимости.
Пользование готовой номограммой не вызывает трудностей (они могут возникнуть лишь при ее построении). Важные свойства номограмм: быстрота нахождения ответов, малая вероятность грубых ошибок, простота решения обратных задач. Номографический расчет не требует специальной подготовки, и для его выполнения, кроме номограмм, необходимы только карандаш и линейка.
Типы номограмм. Применяются следующие номограммы: график функции; сдвоенная шкала (рисунок 48); номограмма сетчатая (рисунок 49); из выровненных точек; циркульная; с параллельным индексом; с крестообразным индексом; барицентрическая; ромбоидальная; транспарантная. Наиболее просты и доступны в работе номограммы с прямолинейными шкалами, они используются, на пример, при расчете и выборе заклепок (см. рисунок 48).
Пояснительный текст к номограмме. В нем указываются зависимости, представленные в виде номограмм; обозначения переменных; способы пользования номограммой; примеры решения задач на номограмме; методика построения номограммы и уравнения их элементов.
Представленная на рисунке 49 номограмма служит для определения количества воды в электролите и заменяет расчет при его приготовлении. Электролит для анодно-механической обработки получается при разбавлении жидкого стекла пресной водой. Пользуются номограммой следующим образом: ареометром определяют удельный вес разбавленного жидкого стекла и по графику находят наклонную прямую, соответствующую замеренному удельному весу. По этой наклонной подбирают такое количество жидкого стекла и соответствующее ему количество воды, чтобы в сумме оно составляло объем бака, в котором приготовляют электролит. Объем бака указан на диагонали сетки.
Предположим, что жидкое стекло имеет удельный вес 1,5 г/см3, а объем бака станка 60 л. Влево по наклонной, соответствующей плотности 1,5, находится точка, которая на горизонтальной оси дает величину 36, а на вертикальной - 24. Таким образом, для приготовления электролита в бак станка следует залить 36 л жидкого стекла и 24 л воды, чтобы получить 60 л электролита.
3. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ГРАФИЧЕСКОГО ЗАДАНИЯ «ВИЗУАЛИЗАЦИЯ ИНФОРМАЦИИ О ПРОЦЕССАХ И ЯВЛЕНИЯХ»
1. Данные по химическому составу сплава представить в табличной форме.
2. Построить диаграммы (два-три типа). Выбрать ту диаграмму(ы), которая(ые), по Вашему мнению, наиболее полно и наглядно отражает передаваемую информацию.
3. Обосновать выбор в текстовой форме объемом не менее 1 страницы.
Задание выполняется в виде реферата на листах белой бумаге (формат А4) с использованием программных средств (AutoCAD): первый лист должен содержать задание в исходной форме; второй и последующие - разработанные таблицы и диаграммы с обоснованием выбора.
ВАРИАНТЫЗАДАНИЙ
| Вариант 1 Сталь 08Х22Н6Т (состав в %): С - 0,08; Мп - 0,8; Si - 0,8; Сr - 22; Ni - 6; S - 0,025; Р - 0,035; Си - 0,3; Ti - 0,65; остальное - Fe. | Вариант 10 Сталь Х20Н80-Н (состав в %): С - 0,06; Мп - 0,6; Si - 1; Сr - 20; S - 0,015; Р - 0,02; Ti - 1,5; А1 - 0,2; Fe - 1; Zn - 0,5; остальное - Ni. |
| Вариант 2 Сталь 20ХГСФЛ (состав в %): С - 0,2; Мп - 1; Si - 0,8; Сr - 0,6; Ni - 0,4; S - 0,03; Р- 0,035; V - 0,1; остальное - Fe. | Вариант 11 Сталь Р9М4К8 (состав в %): С - 1; Мп - 0,3; Si - 0,5; Сr - 3; Ni - 0,1; S - 0,03; Р - 0,03; Мо - 3,8; V - 2,1; Со - 7,5; W - 8,5; остальное - Fe. |
| Вариант 3 Сталь ХН70ВМТЮФ (состав в %): С - 0,12; Мп - 0,5; Si - 0,6; Сr - 15; S - 0,009; Ti - 2; А1 - 2,5; Fe - 5; W - 7; Mo - 4; V - 1; остальное - Ni. | Вариант 12 Сталь Р6М5Ф2К8 (состав в %): С - 0,9; Мп - 0,4; Si - 0,3; Сr - 3,8; Ni - 0,1; S - 0,03; Р - 0,03; Мо - 4,6; V - 1,8; Со - 7,5; W - 5,5; остальное - Fe. |
| Вариант 4 Сталь Р6М5К5 (состав в %): С - 0,9; Мп - 0,5; Si - 0,5; Сr - 4; Ni - 0,4; S - 0,03; Р - 0,03; Мо - 5; V - 2; Со - 5; W - 6; остальное - Fe. | Вариант 13 Сталь 20Х20Н14С2 (состав в %): С - 0,20; Мп - 1,5; Si - 2; Сr - 20; Ni - 14; S-0,025; Р - 0,035; Сu- 0,3; Ti - 0,2; остальное - Fe. |
| Вариант 5 Сталь ХН35ВТЮ (состав в %): С - 0,08; Мп - 0,6; Si - 0,6; Сr - 15; Ti - 3; А1 - 1; Ni - 35; W - 3; остальное - Fe. | Вариант 14 Сталь 4Х5МФ1С (состав в %): С - 0,4; Мп - 0,5; Si - 1; Сr - 5; Ni - 0,35; S - 0,03; Р - 0,03; Мо - 1,5; V - 1; Сu - 0,3; остальное - Fe. |
| Вариант 6 Сплав ХН77ТЮР (состав в %): С - 0,07; Мп - 0,4; Si - 0,6; Сr - 20; S - 0,007; Р - 0,015; Ti - 2,5; А1 - 1; Fe - 1; В - 0,01; остальное - Ni | Вариант 15 Сталь 20ХН4ФА (состав в %): С - 0,2; Мп - 0,5; Si - 0,3; Сr - 1; Ni - 4; S - 0,025; Р - 0,025; V - 0,15; остальное - Fe. |
| Вариант 7 Сталь Р9 (состав в %): С - 0,95; Мп - 0,5; Si - 0,5; Сr - 4; Ni - 0,4; S - 0,03; Р - 0,03; Мо - 1; V - 2,5; Со - 0,5; W - 9; остальное - Fe. | Вариант 16 Сталь 60С2Н2А (состав в %): С - 0,6; Мп - 0,7; Si - 1,5; Сr - 0,3; Ni - 1,5; S - 0,025; Р - 0,025; Сu - 0,2; остальное - Fe. |
| Вариант 8 Сталь Р6М5К5 (состав в %): С - 0,8; Мп - 0,4; Si - 0,3; Сr - 3,8; Ni - 0,1; S - 0,03; Р - 0,03; Мо - 4,8; V - 1,7; Со - 4,8; W - 6; остальное - Fe. | Вариант 17 Сталь 6ХВ2С (состав в %): С - 0,6; Мп - 0,4; Si - 0,8; Сr - 1,3; Ni - 0,35; S - 0,03; Р - 0,03; Мо - 0,3; Сu- 0,3; W - 2,5; остальное - Fe. |
| Вариант 9 Сплав ХН35ВТЮ (состав в %): С - 0,08; Мп - 0,6; Si - 0,6; Сr - 15; Ti - 3; А1 - 1; Ni - 35; W - 3; остальное - Fe. | Вариант 18 Сталь 40Х15Н7Г7Ф2МС (состав в %): С-0,4; Мп-7; Si-1; Сr-15; Ni-7; S-0,02; Р - 0,035; V - 1,5; Мо - 0,95; W - 0,2; Сu - 0,3; остальное - Fe. |
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Антонов А.В. Информация, восприятие и понимание. – Киев: Вища школа, 1998.
2. Бергхаузер Т., Шлив П. Система автоматизированного проектирования AutoCAD: Справочник: Пер. с англ. – М.: Радио и связь, 1999.
3. Боумен У. Графическое представление информации. – М.: Мир, 1971.
4. Единая система конструкторской документации. Общие правила выполнения чертежей. – М.: Издательство стандартов, 2001.
5. ЕСКД. Общие положения. – М.: Издательство стандартов, 2001.
6. Иванцивская Н.Г., Буров В.Г. Графическое моделирование процессов и объектов: Учебное пособие. – Новосибирск: Изд-во НГТУ, 1997.
7. Райан Д. Инженерная графика в САПР. – М.: Мир, 1989.
8. Романычева Э.Т., Соколова Т.Ю., Шандурина Г.Ф. Инженерная и компьютерная графика: – М.: ДМК Пресс, 2001.
9. Буров В.Г. и др. Инженерная графика. Общий курс. М.: Логос, 2004.