Рассчитать нормированную критическую длину основной волны ПВВР (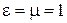
) при 
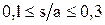и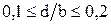 
. Шаг изменения 
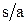и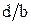 
составляет 0,1. По результатам расчетов постройте график зависимости нормированной критической длины основной волны ПВВР от s/a при различных d/b. Значения 
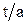=0,4 и 
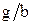=0,7, b/a=0,2. (Вариант 14)
Рассчитаем критическую длину основной волны для ПВВР в программе MATHCAD:
Для s/a=0,1, d/b=0,1:
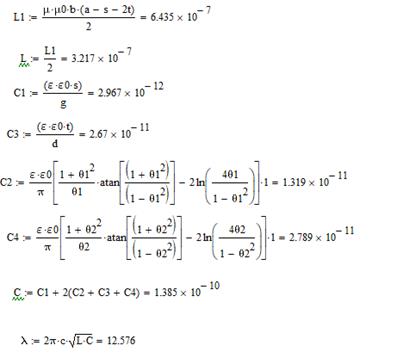
Дальше будем писать только результат длины волны.
Для s/a=0,2, d/b=0,1
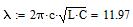
Для s/a=0,3, d/b=0,1
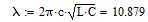
Для s/a=0,1, d/b=0,2
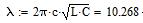
Для s/a=0,2, d/b=0,2
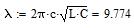
Для s/a=0,3, d/b=0,2
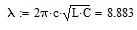
На основании проведённых квазианалитических расчётов построим зависимость нормированной критической длины основной волны ПВВР от s/a при различных d/b:
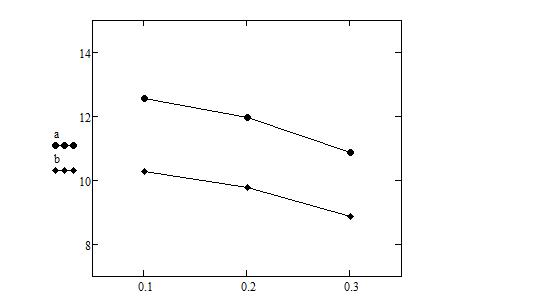
a- d/b =0.1 b - d/b=0/2
Рисунок 4- График квазистационарного расчета критической длины основной волны П-волновода с выступами на ребре
Заключение
В ходе работы был проведен квазианалитический расчет критической длины основной волны ПВВР и НВВР при различных значениях геометрических размеров и параметров диэлектрического заполнения и построен график зависимости длины нормированной критической длины основной волны ПВВР от s/a при различных d/b.
Таким образом, применение рассмотренного в настоящей работе комбинированного численно-аналитического подхода позволило оценить влияние прямоугольных выступов в ПВВР на поперечную электрическую компоненту и критическую длину основной волны. Кроме того, полученная на основе МЭС квазианалитическая зависимость критической длины основной волны ПВВР от размеров поперечного сечения и электрофизических параметров диэлектрического заполнения позволила существенно снизить вычислительные затраты. Необходимо также отметить, что рассмотренные выше квазианалитические выражения могут быть с успехом адаптированы для расчета критической длины основной волны ПВВР с неоднородным диэлектрическим заполнением.
|
|
Список используемой литературы
1. Скворцов А. А. Квазистационарный расчет электродинамических параметров П- и Н волноводов с выступами на ребрах // Радиотехника. 2016. № 7. С. 75–81.
2. Егоров Ю. В. Частично заполненные прямоугольные волноводы. М.: Сов. радио, 1967. 216 с.
3. Скворцов А. А., Торгашов Е. А., Соловьев М. А. Применение П-волновода с выступами на ребре для равномерного нагрева диэлектрических материалов // Проблемы управления, обработки и передачи информации: сб. трудов III Междунар. науч. конф. Саратов: Издат дом «Райт-Экспо», 2013. Т.3. С. 163–169.
4. Волноводы сложных сечений / Г. Ф. Заргано, В. П. Ляпин, В. С. Михалевский и др. М.: Радио и связь. 1986. 124 с.
5. Коломейцев В. А., Комаров В. В., Железняк А. Р. Микроволновые системы с равномерным объемным нагревом. Ч.2. Саратов: Сарат. гос. техн. ун-т, 2006. 232 с.
6. Устройства поляризации радиоволн в терагерцевом диапазоне частот. Новые принципы построения / С. А. Алавердян, С. И. Боков, В. Р. Болов и др. М. Радиотехника: 2012. 256 с.
7. Скворцов А. А., Савина А. Г., Квашнина О. И. Квазистационарная оценка критической длины основной волны П- и Н-волноводов с выступами на ребрах // Радиотехника и связь: материалы IV Междунар. науч.-техн. конф. Саратов: Сар. гос. техн. ун-т, 2007. С. 208–211.
8. Скворцов А. А., Торгашов Е. А., Соловьев М. А. Квазистационарная оценка критической длины первой высшей волны П- и Н-волноводов с выступами на ребрах // Проблемы управления, обработки и передачи информации: сб. трудов II Междунар. науч. конф., Т. 2. Саратов: Сар. гос. техн. ун-т, 2011. С. 123–126
|
|
Лист замечаний