Введение
В квантовой механике существует небольшое число задач, которые имеют физический смысл и могут быть решены точно. Физический смысл имеют следующие основные задачи [2]:
• Задача о движении свободной частицы;
• Гармонический осциллятор;
• Задача о движении в кулоновском потенциале.
Для других взаимодействий не существует точного решения и, следовательно, не существует метода точного решения уравнения Шредингера. В этом случае применяются приближенные методы, такие как: теория возмущений; квазиклассическое приближение; вариационный метод, каждый из которых основан на определенных допущениях [2].
Рассмотрим подробнее теорию возмущений. Аналогично уравнению Шредингера, которое может быть стационарным (если гамильтониан не зависит от времени) или нестационарным (если гамильтониан зависит от времени), теория возмущений также рассматривается различно в стационарном и нестационарном случае [2].
Стационарная теория возмущения
Точное аналитическое решение уравнения Шредингера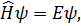 
определяющего энергию и волновые функции стационарных состояний, возможно только для некоторых простейших потенциальных полей, соответствующих идеализированным системам (например, прямоугольная бесконечно глубокая потенциальная яма, линейный гармонический осциллятор, заряженная частица в кулоновском поле точечного заряда). При исследовании реальных атомных и ядерных систем приходится прибегать к приближенным методам вычисления собственных значений и собственных функций гамильтониана. Один из таких методов, не требующий численного интегрирования уравнения Шредингера, квазиклассическое приближение. Другой аналитический метод, называемый теорией возмущений (ТВ), развит для случая, когда гамильтониан ˆ рассматриваемой задачи может быть представлен в виде [1]:
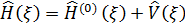(1.1)
где 
гамильтониан идеализированной задачи, допускающей точное аналитическое решение, а 
некоторая малая добавка, называемая оператором возмущения или просто возмущением. Оператором возмущения может быть либо часть гамильтониана, которая не учитывалась в идеализированной задаче, либо потенциальная энергия внешнего воздействия (поля). Задачей теории возмущений является отыскание формул, определяющих энергию и собственные функции гамильтониана 
через известное решение задачи с гамильтонианом 
[1].
Формализм теории возмущений различается в зависимости от того, какое (вырожденное или невырожденное) состояние гамильтониана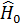 
используется в качестве «нулевого» приближения для решения задачи [1].
Ниже эти случаи рассматриваются раздельно.
Рассмотрение мы начнём с классической теории возмущений. Задача ставится так — имеется гамильтониан 
, где спектр невозмущённого гамильтониана ∣𝑛(0)⟩ = 𝐸(0) ∣𝑛(0)⟩ известен, а матричные элементы возмущения 
— в каком-то смысле малы. Интересуемся же мы устройством спектра полного гамильтониана. Если возмущение действительно мало, то малы и поправки — мы ожидаем, что точные волновые функции и точные уровни энергии |𝑛⟩ = 𝐸n |𝑛⟩ будут параметрически близки к невозмущенным. Идея метода заключается в подстановке в стационарное уравнение Шрёдингера волновых функций и энергий в виде ряда по малому параметру, который содержится в операторе [1]:
+ 
+… 
И в дальнейшем итеративном нахождении этих самых поправок. Сразу отметим, что ряды теории возмущений часто имеют смысл асимптотических рядов, и в действительности чаще всего они расходятся. Это никак не умаляет её ценности — чаще всего точность, которой можно достичь теорией возмущений, вполне достаточна для приложений. Стоит сделать замечание, что условия |𝑛⟩ = 𝐸n |𝑛⟩ недостаточно, чтобы однозначно зафиксировать все поправки теории возмущений — как минимум, необходимо добавить также условие нормировки в произвольном порядке p, которое записывается следующим образом: 
[1].
Невырожденный случай
Пусть значения энергий 
и волновые функции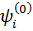 
«невозмущенной» системы с гамильтонианом известны [1]:
(2.1)
Для решения задачи целесообразно переписать исходное стационарное уравнение Шредингера
(2.2)
в энергетическом представлении, выбирая в качестве базиса решение «невозмущенной» задачи (2.1). Разлагая искомую функцию 
по известному базису гамильтониана [1]:
(2.3)
подставляя (2.3) в (2.2) с учетом (2.1), умножая на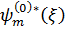 
и интегрируя по 
, вместо дифференциального уравнения (2.2) получаем эквивалентную ему бесконечную систему алгебраических уравнений для коэффициентов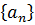 
[1]:
(2.4)
где
(2.5)
— матричный элемент оператора возмущения . В дираковских обозначениях [1]:
; 
; |𝑛⟩ = | 
⟩ (2.6)
Отыскание энергии Е и коэффициентов 
в общем случае сводится к диагонализации бесконечной матрицы системы (2.4). Однако в случае малого спектр 
и собственные функции 
оператора мало отличаются от 
, что позволяет развить достаточно эффективный приближенный метод решения (2.4). Для этого выделим безразмерный малый параметр 
в операторе явно [1]:
, 
, (2.7)
Явный вид этого параметра зависит от конкретной задачи. Пусть, например, 
, где е — заряд электрона, 
— напряженность внешнего электрического поля, действующего на систему с гамильтонианом Но. Вводя боровский радиус 
и атомную единицу напряженности электрического поля 
В/см, можно переписать в виде: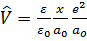 
в случае слабого поля (то есть 
) величина 
может рассматриваться как малый параметр [1].
Будем искать решения матричного уравнения Шредингера (2.4) в виде разложения в ряд по степеням [1]:
; (2.8)
(2.9)
Сущность теории возмущений состоит в последовательном вычислении поправок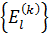 
и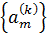 
в разложениях (2.8) и (2.9) с использованием решений уравнения Шредингера для невозмущенной системы [1].
Если состояние невозмущенной системы с энергией 
невырожденное, то и состояние с энергией 
также будет невырожденным, причем 
Поэтому в соответствии с (2.3) в разложении (2.9) необходимо положить [1]:
(2.10)
Дальнейший ход решения задачи состоит в подстановке (2.8)—(2.10) в систему (2.4)
(2.11)
И приравнивании слагаемых с одинаковыми степенями в правой и левой части (2.11). Следует раздельно рассмотреть случаи 
и 
[1]:
1. При получаем первую систему связанных уравнений для 
и 
:
(2.12)
………….
2. При получаем вторую систему, аналогичную (2.12):
(2.13)
…………
Каждое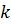 
-е уравнение систем (2.12) и (2.13) соответствует слагаемым порядка 
в (2.4) [1].
Из (2.8), (2.12) следует, что в первом порядке теории возмущений (т.е. учитывая лишь члены порядка ) энергия квантовой системы выражается формулой [1]:
(2.14)
Таким образом, поправка к энергии изолированного уровня в первом порядке теории возмущений равна среднему значению оператора возмущения в соответствующем невозмущенном состоянии [1]:
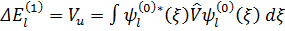(2.15)
Используя первое уравнение (2.13) и соотношение (2.3), находим волновую функцию 
; в первом порядке по величине возмущения [1]:
(2.16)
Штрих над знаком суммы с энергетическим знаменателем означает отсутствие слагаемого с . Это так называемая спектральная сумма. Легко видеть ее ортогональность невозмущенному состоянию. Величина определяется из условия нормировки функции . Функции 
предполагаются нормированными, поэтому из условия нормировки с точностью до 
следует соотношение: 
.Следовательно 
- чисто мнимое (то есть 
, так что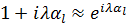 
) и, так как волновые функции определяются с точностью до фазового множителя, можно положить 
. Итак, в первом порядке теории возмущений волновая функция определяется выражением [1]:
(2.17)
Подставляя далее значение а(^ из первого уравнения (2.13) во второе уравнение (2.12), находим величину 
[1]:
Таким образом, во втором порядке теории возмущений энергия 1-го стационарного состояния выражается формулой [1]:
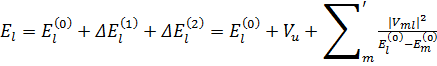(2.18)
Из (2.18) следует, что поправка второго порядка к энергии 
основного состояния всегда отрицательна (энергия 
наименьшая из всех возможных) [1].
Полученные формулы для поправок к энергиям и волновым функциям легко переписать и в дираковских обозначениях [1]:
(2.19)
(2.20)
(2.21)
Формулы (2.19)—(2.21) иногда можно использовать и при наличии вырождения начального состояния с энергией . Пусть невозмущенное значение энергии вырождено с кратностью 
, т. е. 
, где 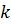= 1,..., , а оператор возмущения в энергетическом представлении диагонален по 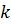, т. е
Физически это означает, что интеграл движения, обусловливающий вы-рождение в невозмущенной задаче, после наложения возмущения по- прежнему остается интегралом движения. В данном случае при 
, 
числители спектральных сумм в (2.20), (2.21) вместе со знаменателями обращаются в 0, т. е. появляется неопределенность Если такие слагаемые положить равными нулю, то при выполнении условия (2.22) можно по-прежнему пользоваться теорией возмущений для невырожденных уровней, рассматривая квантовое число к как параметр. Другими словами, задачу нужно решать независимо для каждого фиксированного значения 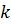, пользуясь теорией возмущений для невырожденных уровней. При этом поправки к энергии могут зависеть от параметра 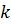(снятие вырождения) [1].
Если в уравнении Шредингера с гамильтонианом (2.1) требуется найти энергию с точностью до первого порядка, поправку к волновой функции вычислять не следует, поскольку для расчета наблюдаемых величин требуется вычисление матричных элементов. При учете поправок к волновой функции в матричных элементах появляются квадратичные по возмущению члены, что является превышением точности. Поэтому в формуле (2.19) при вычислении 
ограничиваются , в (2.21) при нахождении 
в волновой функции оставляют 
и т. д. Зная лишь поправки к волновой функции вплоть до 
, можно получить поправки к энергии до 
[1].
Ряды теории возмущений (2.8), (2.9) могут быть как сходящимися, так и асимптотическими.
В большинстве случаев формулы (2.19)—(2.21) оказываются достаточными для приближенного решения задачи. Условие их применимости сводится, очевидно, к выполнению неравенства [1]:
(2.23)
На практике обычно поступают следующим образом. Вначале находят поправку первого порядка к энергии по формуле (2.19). Если она оказывается ненулевой, решение задачи завершают. Если 
(что может быть обусловлено определенной симметрией оператора 
и функций ) это еще не означает, что поправка отсутствует вообще. В таком случае переходят к вычислению поправки второго порядка к энергии 
и первого порядка к функции и т. д. Как только очередная поправка к энергии 
становится ненулевой, вычисления прекращают. Данная процедура иногда называется поиском поправок в первом неисчезающем порядке теории возмущений [1].