Прежде чем развить метод теории возмущений при наличии вырождения, рассмотрим частный случай предыдущего формализма – случай двух близких уровней. Он позволяет исследовать также и особенности решения задачи при наличии двукратного вырождения невозмущенного значения энергии  [1].
[1].
Из формул (2.20), (2.21) следует, что если среди собственных значений гамильтониана  есть одно или несколько близких к
есть одно или несколько близких к  (настолько, что для них перестает выполняться условие (2.23)), то поправки к волновой функции и энергии -го уровня будут велики из-за малости энергетических знаменателей, и пользоваться этими формулами нельзя. Если, однако, число собственных значений
(настолько, что для них перестает выполняться условие (2.23)), то поправки к волновой функции и энергии -го уровня будут велики из-за малости энергетических знаменателей, и пользоваться этими формулами нельзя. Если, однако, число собственных значений  , близких к
, близких к  , невелико, то можно изменить метод вычислений так, чтобы исключить появление больших поправок. Покажем это на примере двух близких уровней [1].
, невелико, то можно изменить метод вычислений так, чтобы исключить появление больших поправок. Покажем это на примере двух близких уровней [1].
Пусть оператор  , имеет два близких собственных значения
, имеет два близких собственных значения 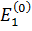 и
и
 , которым соответствуют собственные функции
, которым соответствуют собственные функции  и
и  , а все остальные собственные значения расположены далеко от них. При вычислении поправки к волновой функции по формуле (2.20) мы убедимся, что из-за малого знаменателя
, а все остальные собственные значения расположены далеко от них. При вычислении поправки к волновой функции по формуле (2.20) мы убедимся, что из-за малого знаменателя 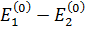 вклад функции
вклад функции  будет велик. Поэтому целесообразно уже в нулевом приближении искать решение в виде линейной комбинации невозмущенных волновых функций, соответствующих близким энергиям [1]:
будет велик. Поэтому целесообразно уже в нулевом приближении искать решение в виде линейной комбинации невозмущенных волновых функций, соответствующих близким энергиям [1]:
 (3.1)
(3.1)
т. е. ограничиться в энергетическом представлении только вкладом состояний |1⟩ и |2⟩. Стационарное уравнение Шредингера в таком упрощенном представлении принимает вид системы двух алгебраических уравнений [1]:

 (3.2)
(3.2)
Где  , m,n = 1,2. (3.3)
, m,n = 1,2. (3.3)
Из условия нетривиальной разрешимости системы (3.2) находим два значения энергии [1]:
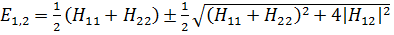 (3.4)
(3.4)
Рис. 2.1. Энергии  и
и 
Где знак «плюс» относится к уровню  , а «минус» — к
, а «минус» — к  . Если для данных состояний выполняется условие [1]:
. Если для данных состояний выполняется условие [1]:
 (3.5)
(3.5)
то из (3.4) следуют значения энергии
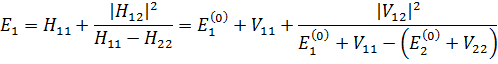

совпадающие с точностью до слагаемых  с результатом теории возмущений для невырожденных уровней (2.18).
с результатом теории возмущений для невырожденных уровней (2.18).
Для противоположного (3.5) условия [1]:
 (3.6)
(3.6)
имеем:
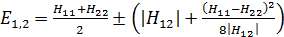 (3.7)
(3.7)
На рис. 2.1. на основе формулы (3.4) показаны энергии  и
и  как функции разности
как функции разности  для некоторого фиксированного значения
для некоторого фиксированного значения 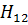 . Значения
. Значения  и
и 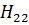 указаны штриховыми линиями. Поправки второго порядка к значениям энергии изображаются на рисунке разностью между сплошной и ближайшей штриховой линией. Интересно, что поправки второго порядка к значениям
указаны штриховыми линиями. Поправки второго порядка к значениям энергии изображаются на рисунке разностью между сплошной и ближайшей штриховой линией. Интересно, что поправки второго порядка к значениям  и
и 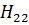 всегда увеличивают расстояния между уровнями. В связи с этим иногда говорят об «отталкивании уровней», понимая под этим явлением увеличение расстояния между двумя близкими уровнями, когда в операторе Гамильтона учитываются слагаемые, которые отбрасываются в более упрощенной задаче [1].
всегда увеличивают расстояния между уровнями. В связи с этим иногда говорят об «отталкивании уровней», понимая под этим явлением увеличение расстояния между двумя близкими уровнями, когда в операторе Гамильтона учитываются слагаемые, которые отбрасываются в более упрощенной задаче [1].
Рис. 2.1. Энергии  и
и 
Из уравнений (2.25) можно найти отношение коэффициентов а и b, определяющих волновую функцию (2.24) [1]:
 ,
, 
Где  (3.8)
(3.8)
Таким образом, нормированные волновые функции состояний, соответствующих энергиям  и
и  , будут иметь вид [1]:
, будут иметь вид [1]:

 (3.9)
(3.9)
Если выполняется условие (3.5), то из (3.8) следует, что  и
и
 ,
,  , т.е. при наличии возмущения одно из невозмущенных состояний будет давать доминирующий вклад (другими словами, уровни
, т.е. при наличии возмущения одно из невозмущенных состояний будет давать доминирующий вклад (другими словами, уровни 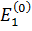 и
и  фактически будут «далекими»). Наоборот, если выполняется условие (2.29), то
фактически будут «далекими»). Наоборот, если выполняется условие (2.29), то  , поэтому
, поэтому  и
и  выступают в (3.9) с равными долями (это и есть случай «истинно близких» уровней в узком смысле слова) [1].
выступают в (3.9) с равными долями (это и есть случай «истинно близких» уровней в узком смысле слова) [1].
Если теперь для отыскания поправок к энергии  (или
(или  ) и волновой функции
) и волновой функции  (или
(или  ) использовать найденные в нулевом приближении уровни энергии
) использовать найденные в нулевом приближении уровни энергии  и волновые функции
и волновые функции 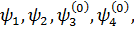 то в энергетических знаменателях спектральных сумм (2.20), (2.21) не будет встречаться малая разность
то в энергетических знаменателях спектральных сумм (2.20), (2.21) не будет встречаться малая разность  , так как числитель соответствующего слагаемого
, так как числитель соответствующего слагаемого  равен нулю в силу того, что обе функции
равен нулю в силу того, что обе функции  и
и  являются решениями стационарного уравнения Шредингера с полным гамильтонианом (2.1). Следовательно, определение поправок более высокого порядка можно далее вести обычным методом теории возмущений для невырожденных «далеких» уровней [1].
являются решениями стационарного уравнения Шредингера с полным гамильтонианом (2.1). Следовательно, определение поправок более высокого порядка можно далее вести обычным методом теории возмущений для невырожденных «далеких» уровней [1].
Вырожденный случай
Результаты предыдущего параграфа остаются справедливыми и при совпадении энергии двух уровней, т. е. при наличии двукратного вырождения ( ). Легко обобщить эти результаты и на случай -кратного вырождения уровня
). Легко обобщить эти результаты и на случай -кратного вырождения уровня  . Соответствующие невозмущенные волновые функции теперь нужно снабдить дополнительным индексом
. Соответствующие невозмущенные волновые функции теперь нужно снабдить дополнительным индексом 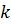 = 1,2,...,
= 1,2,...,  [1]:
[1]:

Рассмотрим теперь случай, когда условие (2.22) не выполняется. Тогда необходимо отказаться от (2.10) и в качестве функции нулевого приближения взять линейную комбинацию
 (4.1)
(4.1)
Другими словами, воспользуемся «редуцированным» энергетическим представлением, ограничившись лишь невозмущенными вырожденными состояниями, относящимися к одному и тому же уровню  . В этом представлении после подстановки (4.1), умножения на
. В этом представлении после подстановки (4.1), умножения на  и интегрирования по
и интегрирования по  уравнение Шредингера с гамильтонианом (2.1) превращается в систему
уравнение Шредингера с гамильтонианом (2.1) превращается в систему  линейных однородных алгебраических уравнений относительно
линейных однородных алгебраических уравнений относительно  [1]:
[1]:
 (4.2)
(4.2)
где  ;
;
 — подлежащее определению «возмущенное» значение энергии.
— подлежащее определению «возмущенное» значение энергии.
Условием нетривиальной разрешимости системы (4.2) является обращение в нуль ее детерминанта [1]:
 (4.3)
(4.3)
Раскрывая определитель в левой части (4.3), получим уравнение степени  относительно
относительно  (оно называется вековым, или секулярным). Ввиду эрмитовости матрицы
(оно называется вековым, или секулярным). Ввиду эрмитовости матрицы 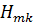 это уравнение имеет
это уравнение имеет  вещественных корней. Если все корни различны, то
вещественных корней. Если все корни различны, то  -кратно вырожденный уровень
-кратно вырожденный уровень  невозмущенной системы расщепляется на
невозмущенной системы расщепляется на  различных подуровней
различных подуровней  (полное снятие вырождения возмущением
(полное снятие вырождения возмущением  ), n-му подуровню будет соответствовать функция [1]:
), n-му подуровню будет соответствовать функция [1]:
 (4.4)
(4.4)
Коэффициенты  которой определяются из системы уравнений (3.1) при подстановке вместо
которой определяются из системы уравнений (3.1) при подстановке вместо  значения
значения 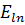 , найденного из (4.3). Нормированные функции (4.4) называются правильными функциями нулевого приближения. Если же один или несколько корней уравнения являются кратными, то вырождение снимается частично. При этом волновые функции (4.4) определяются неоднозначно. Каждому g-кратному корню уравнения (4.3) будут соответствовать g линейно независимых комбинаций (4.4), которые тем не менее можно ортогонализовать [1].
, найденного из (4.3). Нормированные функции (4.4) называются правильными функциями нулевого приближения. Если же один или несколько корней уравнения являются кратными, то вырождение снимается частично. При этом волновые функции (4.4) определяются неоднозначно. Каждому g-кратному корню уравнения (4.3) будут соответствовать g линейно независимых комбинаций (4.4), которые тем не менее можно ортогонализовать [1].
Развитая в данном разделе техника применима и при выполнении условия (2.22). При этом, однако, матрица 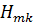 будет диагональной и можно пользоваться более простыми формулами.
будет диагональной и можно пользоваться более простыми формулами.
Легко заметить, что правильные функции нулевого приближения (4.4) приводят к появлению поправок первого порядка к уровню  [1].
[1].
Для получения поправок более высокого порядка в спектральные суммы (2.20), (2.21) необходимо включить состояния, относящиеся к другим невозмущенным энергетическим уровням. В частности, поправки второго порядка к энергии -кратно вырожденного уровня  при нулевых матричных элементах
при нулевых матричных элементах  также вычисляются из решения секулярного уравнения (4.3), в котором производится замена [1]:
также вычисляются из решения секулярного уравнения (4.3), в котором производится замена [1]:
 .
.
Суммирование не распространяется на вырожденные состояния, принадлежащие уровню  [1].
[1].
Заключение
Стационарная теория возмущений является одним из приближенных методов, которые используются в квантовой механике. Стационарная теория возмущений основана на точном решении задачи на собственные значения для некоторого оператора. Данная теория применима, когда возмущение не слишком искажает невозмущенный спектр, а гамильтониан не зависит от времени. Стационарная теория возмущений основана на точном решении задачи на собственные значения для некоторого оператора. Для остальных случаев используются другие методы.
Список литературы
1. Копытин И.В. Квантовая теория. Курс лекций. Часть 2/ И.В. Копытин, А.С. Корнев, Н.Л. Манаков, М.В. Фролов. Воронеж: Издательско-полиграфический центр ВГУ, 2007, 76 с.
2. Ферми Э. Лекции по квантовой механике/ Э. Ферми. Ижевск: НИЦ «Регулярная и хаотическая динамика». 2000, 248 с.