Глава 3. Интегрирование ФКП
Определение интеграла от ФКП, вычисление и свойства
Пусть l – дуга направленной кусочно–гладкой кривой, уравнение которой 
где 
, лежащей в плоскости (z). Пусть на l лежат точки А и В. Кривая направлена, значит на ней задано направление: при возрастании t точка перемещается от т. А к т. В. Пусть на кривой задана однозначная и непрерывная ФКП 
. Разобьем дугу АВ произвольным образом точками 
на n элементарных дуг, 
, соответствующим значениям параметра: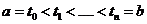 
. Обозначим 
. Выберем на каждой элементарной дуге по точке 
, и составим интегральную сумму: 
.
Определение 44. Если существует конечный предел интегральной суммы при 
, который не зависит ни от способа разбиения дуги на элементарные дуги, ни от выбора на них точек , то он называется интегралом от функции по дуге кривой l и обозначается 
.
Теорема 9 (существования). Если функция непрерывна на l, то интеграл от нее по дуге l существует.
Рассмотрим функцию 
, где 
Отсюда 
Тогда 
интегральная сумма запишется в виде: 
.
Перейдем к пределу при 
и получим формулу для вычисления интеграла:
. (18)
В результате получили полную аналогию между криволинейными интегралами 2-го рода и интегралами от ФКП. Таким образом, вычисление интеграла от ФКП сводится к вычислению двух криволинейных интегралов.
Свойства
1. 
.
2. 
.
3. 
.
4. 
, 
.
5. 
.
6. Если – аналитическая функция, то интеграл 
не зависит от пути интегрирования l.
Замечание. Если дуга l задана параметрическим уравнением 
, где 
, то 
. Если дуга – окружность с центром в начале координат или часть окружности, то удобнее представить ее уравнение в виде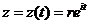 
.
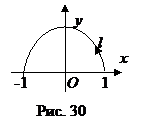Пример 1. Вычислить 
, где l – верхняя полуокружность 
с обходом против часовой стрелки (рис. 30).
Решение.
, тогда 
, 
.
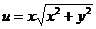, тогда 
.
Подставим в формулу (18) для вычисления интеграла.
.
Если в примере окружность задать параметрическим уравнением: 
, где 
, а 
, то интеграл преобразуется к виду:
.
Замечание. При интегрировании многозначной функции необходимо выделять ее однозначную ветвь. Это достигается обычно заданием значения многозначной функции в некоторой точке контура интегрирования.
Пример 2. Вычислить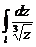 
по заданному контуру 
, где одно из значений корня 
.
Решение.
– многозначная функция. Представим ее в показательной форме: 
.
В условии задачи рассматривается 
, причем , следовательно, 
. Тогда имеем, что 
, (*)
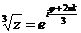где 
Для интегрирования необходимо выделить однозначную ветвь заданной функции , т.е. найти значение k. Для этого применим заданное значение многозначной функции в точке z = 1: (**)
Найдем значение корня 
в тригонометрической форме: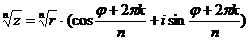 
.
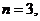
следовательно, 
. Тогда получим, что 
. (***)
Сравним выражения (**) и (***):
условию (**) удовлетворяет та однозначная ветвь функции, для которой k = 1. Подставим k = 1 в (*):
.
Запишем переменную z в показательной форме: 
, а так как по условию 
, то 
. Найдем дифференциал dz: 
.
Пределы интегрирования даны в условии задачи: 
.
Подставим найденные , z, dz в исходный интеграл:
.
Теорема Коши. Интегральная формула Коши
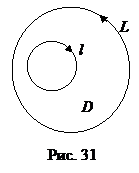
Теорема 10 (теорема Коши). Если функция однозначная аналитическая функция в односвязной области D, ограниченной контуром L и l – замкнутый контур в области D (рис. 31), то
(19)
Если, дополнительно, функция – непрерывна в замкнутой области 
, то
(20)
Доказательство (19).
По формуле (18) 
. В силу аналитичности функции функции u (x, y) и v (x, y) образуют гармоническую пару, для которой справедлива теорема 6: 
. Следовательно, , что и требовалось доказать.