Введение.
Операционное (символическое) исчисление применяется для решения линейных обыкновенных дифференциальных уравнений и уравнений с частными производными, дифференциально-разностных уравнений и интегральных уравнений типа свертки, к которым приводятся задачи главным образом по переходным процессам линейных физических систем электротехники, радиотехники, импульсной техники, теории автоматического регулирования и других отраслей науки и техники.
Метод символического исчисления основан на том, что над оператором дифференцирования  и некоторыми функциями этого оператора производится определенная система действий. В этой системе действий дифференцирование функции
и некоторыми функциями этого оператора производится определенная система действий. В этой системе действий дифференцирование функции 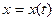 рассматривается как умножение оператора
рассматривается как умножение оператора  на функцию
на функцию  этого оператора
этого оператора 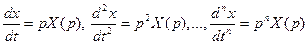 , а интегрирование как деление на оператор
, а интегрирование как деление на оператор  функции этого оператора
функции этого оператора  .
.
I.ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ.
1.Оригинал и изображение.
Определение. Оригиналом называется функция  , определенная на всей числовой оси
, определенная на всей числовой оси  и удовлетворяющая следующим условиям:
и удовлетворяющая следующим условиям:
1.  непрерывна во всей области определения, за исключением, может быть, конечного числа точек разрыва I рода на каждом отрезке конечной длины;
непрерывна во всей области определения, за исключением, может быть, конечного числа точек разрыва I рода на каждом отрезке конечной длины;
2.  при
при 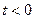 ;
;
3.  при
при  возрастает не быстрее некоторой экспоненциальной функции, то есть существуют такие числа
возрастает не быстрее некоторой экспоненциальной функции, то есть существуют такие числа  , что для всякого
, что для всякого  выполняется неравенство
выполняется неравенство  , где наименьшее из чисел
, где наименьшее из чисел  , при котором выполняется неравенство, называется показателем роста оригинала.
, при котором выполняется неравенство, называется показателем роста оригинала.
Замечание 1. Оригинал  может принимать действительные значения и может быть комплексной функцией действительного переменного, то есть иметь вид
может принимать действительные значения и может быть комплексной функцией действительного переменного, то есть иметь вид  Каждая из функций
Каждая из функций  должны удовлетворять условиям оригинала.
должны удовлетворять условиям оригинала.
Замечание 2. В дальнейшем для краткости записи будем писать  . Под этим будем понимать следующее:
. Под этим будем понимать следующее:

Пример 1. Показать, что функция

является оригиналом.
Решение. 1) Функция  непрерывна для
непрерывна для 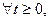
2) она равна нулю при 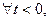
3)  .
.
Оценим модуль этой функции

Таким образом,  Так как функция
Так как функция  удовлетворяет всем требованиям, предъявляемым к оригиналу, то она является оригиналом.
удовлетворяет всем требованиям, предъявляемым к оригиналу, то она является оригиналом.
Пример 2. Функция  не является оригиналом, так как при
не является оригиналом, так как при  имеет разрыв второго рода.
имеет разрыв второго рода.
Если  - оригинал, то, очевидно,
- оригинал, то, очевидно,  будет оригиналом с тем же показателем роста;
будет оригиналом с тем же показателем роста;
-линейная комбинация оригиналов – есть оригинал;
-если  - оригинал, то
- оригинал, то  (
( - положительное число),
- положительное число),  (
( - действительное число),
- действительное число),  (
( - комплексное число),
- комплексное число),  тоже будут оригиналами.
тоже будут оригиналами.
Определение. Изображением функции  называется функция
называется функция  комплексного переменного
комплексного переменного 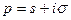 , которая определяется равенством
, которая определяется равенством
 (1)
(1)
Интеграл (1) называется интегралом Лапласа функции  . Операция перехода от оригинала
. Операция перехода от оригинала  к изображению
к изображению  называется преобразованием Лапласа. Теория преобразования Лапласа называют операционным исчислением. Тот факт, что
называется преобразованием Лапласа. Теория преобразования Лапласа называют операционным исчислением. Тот факт, что  и
и  относятся друг к другу как оригинал и изображение, записывают так:
относятся друг к другу как оригинал и изображение, записывают так:  или
или 
Можно доказать, что при выполнении условий 1-3 для функции  несобственный интеграл
несобственный интеграл  сходится абсолютно и равномерно при
сходится абсолютно и равномерно при 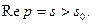
Упражнения. Проверить, какие из указанных функций являются функциями-оригиналами:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11. 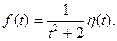
Ответ: 1.да; 2.да; 3. нет; 4. да; 5. да; 6. нет; 7. нет; 8. да; 9. нет; 10. да; 11.да.
2. Единичная функция Хевисайда и ее изображение.
Определение. Единичной функцией Хевисайда называется функция вида
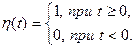
График функции имеет вид

Любой оригинал  при помощи единичной функции
при помощи единичной функции  может быть записан в виде
может быть записан в виде  . Легко показать, что
. Легко показать, что  является оригиналом. Найдем его изображение. Для этого применим преобразование Лапласа
является оригиналом. Найдем его изображение. Для этого применим преобразование Лапласа

Найдем  . Так как
. Так как 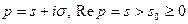 , а
, а  , то
, то  Таким образом,
Таким образом, 
3. Некоторые теоремы об изображении.
Теорема 1 (о существовании изображения).
Всякий оригинал  имеет своим изображением функцию комплексного переменного
имеет своим изображением функцию комплексного переменного  , определенную в полуплоскости
, определенную в полуплоскости  , где
, где  - показатель роста оригинала (рис.1).
- показатель роста оригинала (рис.1).

Рис.1.
Теорема 2 (о поведении изображения на бесконечности).
Если функция  - изображение, то
- изображение, то 
Для этой теоремы нет обратной, то есть из условия
 не следует, что
не следует, что  -изображение.
-изображение.
Пример 1. Функции  не стремятся к нулю при
не стремятся к нулю при  и поэтому не могут служить изображениями.
и поэтому не могут служить изображениями.
Пример 2. Функция  при
при  , но не существует функции
, но не существует функции  , для которой
, для которой  было бы
было бы
изображением.
Теорема 3 (о линейности изображения)
Если  и
и  , то
, то  , где
, где  - комплексные постоянные.
- комплексные постоянные.
Теорема 4(об аналитичности изображения)
Если функция  является изображением некоторого оригинала
является изображением некоторого оригинала  , то
, то  - функция аналитическая в полуплоскости
- функция аналитическая в полуплоскости  , где
, где  - показатель роста оригинала.
- показатель роста оригинала.
4. Изображение простейших оригиналов
1. Пусть  , где
, где  Тогда
Тогда  , то есть
, то есть  Действительно, так как
Действительно, так как  при
при  , то на основании теоремы 3 имеем
, то на основании теоремы 3 имеем  при
при  .
.
2. 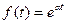 . Найдем
. Найдем  по определению
по определению

если  , и
, и 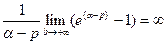 , если
, если 
Таким образом  если
если 
3.  , (
, ( - положительное число). Выразим косинус через показательные функции:
- положительное число). Выразим косинус через показательные функции: 
Зная, что  при
при  , и учитывая свойство линейности изображения, получим
, и учитывая свойство линейности изображения, получим

Так как в данном случае  , то
, то  , и, следовательно,
, и, следовательно,  при
при  .
.
4.  , (
, ( - положительное число). Проводя рассуждения, аналогичные предыдущим, и учитывая, что
- положительное число). Проводя рассуждения, аналогичные предыдущим, и учитывая, что  , получим
, получим
 при
при  .
.
5.  , (
, ( - положительное число). Запишем
- положительное число). Запишем  в виде:
в виде:  Тогда
Тогда
 ,
,
при  .
.
 при
при  .
.
6.  , (
, ( - положительное число). Используя формулу
- положительное число). Используя формулу  , получим
, получим
 при
при  .
.
Пример. Найти изображение заданных функций
а)  ; б)
; б)  в)
в)  ; г)
; г)  .
.
Решение.
а) 

б) 
в) 

г) 
Упражнения. Пользуясь определением, найти изображения следующих функций:
1. 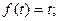 2.
2.  3.
3.  4.
4. 
Ответы: 1.  2.
2. 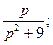 3.
3.  4.
4. 
II ОСНОВНЫЕ ТЕОРЕМЫПРЕОБРАЗОВАНИЯ ЛАПЛАСА
1. Теорема подобия
Если  , то
, то 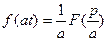 для любого
для любого 
Пример. Найти изображение следующих функций:
а)  ; б)
; б) 
Решение. а) Преобразовав  по формулам тригонометрии, получим
по формулам тригонометрии, получим  , и, следовательно,
, и, следовательно,

б) Аналогично,
 Упражнения. Пользуясь теоремами линейности и подобия, найти изображения следующих функций:
Упражнения. Пользуясь теоремами линейности и подобия, найти изображения следующих функций:
1.  2.
2. 
3.  4.
4. 
Ответы: 1.  2.
2. 
3.  4.
4. 
2. Теорема смещения
Если  , то
, то  для любого
для любого  при
при 
Пример 1. Найти изображение функций:
а)  б)
б)  в)
в)  г)
г) 
Решение. Так как 
 то применяя теорему смещения, получим:
то применяя теорему смещения, получим:
а)  б)
б) 
в)  г)
г)  .
.
Пример 2. Найти изображение функции 
Решение. Представим  в виде:
в виде:

Тогда 
= 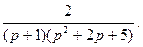
Упражнения. Найти изображения функций:
1. 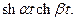 2.
2.  3.
3. 
4. 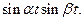 5.
5.  6.
6. 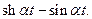
7.  8.
8.  9.
9. 
10.  11.
11. 
Ответы: 1. 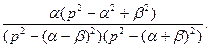
2. 
3. 
4. 
5.  6.
6.  7.
7. 
8. 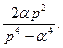 9.
9.  10.
10. 
11. 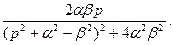
3. Теорема запаздывания
Если  , то
, то  для любого
для любого  .
.
По определению оригинала имеем:

График функции  сдвинут по оси
сдвинут по оси  относительно графика функции
относительно графика функции  на величину
на величину  . Процесс, описываемый функцией
. Процесс, описываемый функцией  , начинается как бы с опозданием на время
, начинается как бы с опозданием на время  , относительно процесса, описываемого функцией
, относительно процесса, описываемого функцией  . Отсюда и появился термин «запаздывание». Исходя из физического толкования, теорему запаздывания можно сформулировать так: запаздывание оригинала на положительную величину
. Отсюда и появился термин «запаздывание». Исходя из физического толкования, теорему запаздывания можно сформулировать так: запаздывание оригинала на положительную величину  соответствует умножению изображения на
соответствует умножению изображения на  .
.
Пример 1. Найти изображение функции 
Решение. Запишем функцию в виде

График этой функции имеет вид

Рис.2.
Так как изображением функции  является
является  , то используя теорему запаздывания, получим
, то используя теорему запаздывания, получим 
Пример 2. Найти изображение функции

Решение.

Пример 3. Найти изображение функции 
Решение. Представим функцию  в виде
в виде

Тогда 
Теорема запаздывания является удобным способом для нахождения изображений кусочно-непрерывных оригиналов, заданных графически.
Пример 1. Найти изображение функции, заданной графически:

Запишем аналитическое выражение для функции 

Функцию  с помощью обобщенной единичной функции можно записать формулой:
с помощью обобщенной единичной функции можно записать формулой: 
Находим изображение оригинала  Имеем
Имеем  , так как
, так как 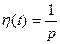 и
и 
Пример 2. Найти изображение функции

Решение. Построим график функции 

Используя функцию Хевисайда, запишем  в виде:
в виде:

Теперь перейдем от оригинала к изображению, используя теорему запаздывания:
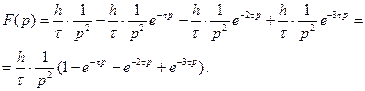
Упражнения. Найти изображения следующих функций, заданных графически:


1. 2.


3. 4.


5.
6.
Ответы: 1.  2.
2.  3.
3. 
4. 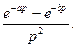 5.
5.  6.
6. 
Пример 3. Найти изображение периодической с периодом  функции
функции  .
.
Решение. Введем функцию

Тогда  , так как
, так как  при
при  , в силу периодичности. Переходя к изображениям, получим:
, в силу периодичности. Переходя к изображениям, получим:
 , где
, где 
Следовательно, 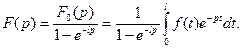
Пример 4. Найти изображения периодических функций:
1. 

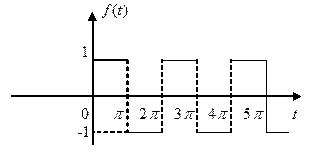 Решение. Функция
Решение. Функция  имеет много общего с тригонометрической функцией
имеет много общего с тригонометрической функцией  , поэтому она называется прямоугольным синусом.
, поэтому она называется прямоугольным синусом.
Находим изображение  .
.
Получим

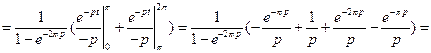

или 
Пример 5. Найти изображение периодической функции



Перейдя к изображению, получаем
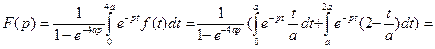
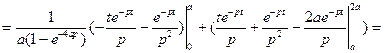
 или
или  .
.
Упражнения. Найти изображения периодических функций:
1. 

2. 

3. 

4. 

5. 

Ответы: 1.  2.
2.  3.
3. 
4.  5.
5. 
Дифференцирование оригинала
Если  и существует функция
и существует функция 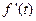 , являющаяся оригиналом, то
, являющаяся оригиналом, то
 , где
, где  .
.
Предположим теперь, что 
 -раз непрерывно дифференцируемая на
-раз непрерывно дифференцируемая на  функция и
функция и  является оригиналом. Тогда, используя полученное соотношение
является оригиналом. Тогда, используя полученное соотношение  , получим:
, получим:




Следствие. Если начальные условия нулевые, то есть  ,то
,то 
Пример 1. Зная, что  , найти изображение для функции
, найти изображение для функции  .
.
Решение. Так как 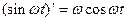 , то
, то

Отсюда:  .
.
Пример 2. Найти изображения дифференциальных выражений при заданных начальных условиях:
а) 
б) 
Решение. По теореме дифференцирования оригинала имеем:
а) 
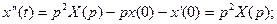

Тогда

б) 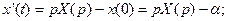

Тогда
 Упражнения. Найти изображения дифференциальных выражений при заданных начальных условиях:
Упражнения. Найти изображения дифференциальных выражений при заданных начальных условиях:
1. 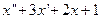 при условии
при условии  .
.
2.  при условии
при условии 


3.  при условии
при условии 
4.  при условии
при условии  .
.
5.  при условии
при условии  .
.
5. Интегрирование оригинала
Если  , то
, то 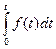 является оригиналом и имеет место соотношение
является оригиналом и имеет место соотношение 
Таким образом, интегрирование оригинала соответствует делению на  изображения подынтегральной функции.
изображения подынтегральной функции.
Пример 1. Найти изображение оригинала  .
.
Решение. Так как  , то
, то  .
.
Пример 2. Найти изображение оригинала  .
.
Решение. Преобразуем 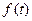 следующим образом
следующим образом
 .
.
Тогда  .
.
Упражнения.
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
Ответы: 1.  . 2.
. 2. 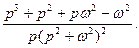 3.
3. 
4.  5.
5. 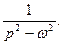 6.
6. 