Если  , то
, то  .
.
Следствие. Используя это свойство легко получить следующие соотношения: 


В частности, если  , то
, то 
Таким образом,  .
.
Пример 3. Найти изображение функций:
а)  б)
б) 
Решение. а) Так как изображение оригинала  , то
, то
 Или
Или  .
.
б) Имеем  . Тогда по следствию
. Тогда по следствию 

Упражнения. Найти изображения следующих функций:
1.  2.
2.  3.
3. 
4. 
Ответы: 1. 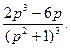 2.
2.  3.
3. 
4. 
7. Интегрирование изображения.
Если  и
и  является оригиналом, то имеет место соотношение
является оригиналом, то имеет место соотношение 
Пример 1. Найти изображение функции  .
.
Решение. Известно, что  Тогда
Тогда 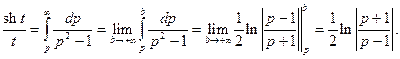
Таким образом, 
Пример 2. Найти изображения функций:
1.  (интегральный синус)
(интегральный синус)
2.  (интегральный гиперболический синус).
(интегральный гиперболический синус).
Решение.
1. Из равенства  , по теореме интегрирования изображения, имеем
, по теореме интегрирования изображения, имеем  Отсюда, по теореме интегрирования оригинала, получим
Отсюда, по теореме интегрирования оригинала, получим 
2. Имеем  или
или

Упражнения.
1.  2.
2.  3.
3.  4.
4.  5.
5. 
6.  7.
7. 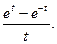
Ответы: 1.  2.
2.  3.
3. 
4.  5.
5.  6.
6.  7.
7. 
Свертка функций. Свойства свертки. Изображение свертки.
1) Пусть  и
и  - непрерывные функции на
- непрерывные функции на 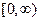 .
.
Определение. Сверткой функций  и
и  ,
,  называется функция от
называется функция от  обозначаемая
обозначаемая  и определяемая интегралом вида
и определяемая интегралом вида 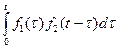 , то есть
, то есть
 =
=  .
.
Пример. Найти свертку функций  .
.
Решение. 
2) Свойства свертки.
а) Коммутативность.
Выражение для свертки функций не зависит от порядка, в котором берутся эти функции, то есть  =
= 
или  =
=  .
.
б) Ассоциативность: 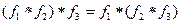 .
.
в) Рефлексивность:  .
.
г) Если  и
и  - оригиналы, то их свертка
- оригиналы, то их свертка 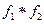 - тоже оригинал.
- тоже оригинал.
Пример. Для оригиналов 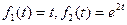 проверить свойство коммутативности свертки.
проверить свойство коммутативности свертки.
Решение. Найдем

Аналогично
 Таким образом,
Таким образом,  =
=  .
.
3) Теорема Э.Бореля (теорема умножения изображений).
Если  и
и  , то свертке функций
, то свертке функций  соответствует произведение изображений.
соответствует произведение изображений.
 =
=  , где
, где 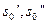 - показатели роста оригиналов
- показатели роста оригиналов  и
и  .
.
Пример. Найти изображение свертки следующих оригиналов:
а)  б)
б) 
в) 
Решение. а) Так как  , то
, то

б) Аналогично,  , поэтому
, поэтому

 .
.
в) Данный интеграл можно рассматривать как свертку оригиналов  и
и  . Известно, что
. Известно, что  , и, следовательно,
, и, следовательно,
 =
=  .
.
Интеграл Дюамеля
Пусть  и
и  - оригиналы, непрерывные и дифференцируемые на
- оригиналы, непрерывные и дифференцируемые на  ,
,  являются оригиналами. Тогда, если
являются оригиналами. Тогда, если  и
и  , то
, то
 .
.
Эта формула называется формулой Дюамеля и применяется для решения дифференциальных уравнений с постоянными коэффициентами. Интеграл, стоящий слева называется интегралом Дюамеля. В силу свойства коммутативности свертки формула Дюамеля может быть записана также в виде
 ;
;
 ;
;
 .
.
III. ФОРМУЛЫОБРАЩЕНИЯ ЛАПЛАСА
Формула, позволяющая по известному изображению  определить ее оригинал
определить ее оригинал  , называется формулой обращения. Общий способ нахождения оригинала по данному изображению дают следующие теоремы:
, называется формулой обращения. Общий способ нахождения оригинала по данному изображению дают следующие теоремы:
1.Теорема обращения. Теорема единственности.
Если  - оригинал, а
- оригинал, а  - его изображение, то во всех точках непрерывности оригинала имеет место соотношение
- его изображение, то во всех точках непрерывности оригинала имеет место соотношение
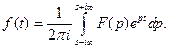 (2)
(2)
Здесь интегрирование производится по любой бесконечной прямой 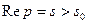 , лежащей в полуплоскости абсолютной сходимости интеграла Лапласа от функции
, лежащей в полуплоскости абсолютной сходимости интеграла Лапласа от функции  ,
, 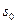 - показатель роста оригинала (рис.3). Формула (2) носит название формулы Римана-Меллина
- показатель роста оригинала (рис.3). Формула (2) носит название формулы Римана-Меллина

Теорема единственности. Если два оригинала 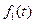 и
и 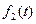 имеют одно изображение
имеют одно изображение 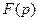 , то функции
, то функции 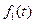 и
и  совпадают во всех точках непрерывности.
совпадают во всех точках непрерывности.
Замечание. Непосредственное применение формулы обращения часто затруднительно, и обычно применяют теоремы разложения, являющиеся следствиями из нее.
2. Обобщенная теорема разложения.
Если  - изображение, то его оригинал может быть найден по формуле
- изображение, то его оригинал может быть найден по формуле  , где
, где  - особые точки функции
- особые точки функции 
3. Нахождение оригинала для дробно-рационального изображения.
При нахождении оригинала для изображения, являющегося правильной рациональной дробью вида  , где
, где  и
и  - полиномы, можно пользоваться теоремами:
- полиномы, можно пользоваться теоремами:
Теорема 1. Если изображение является правильной рациональной дробью, то есть  , где
, где  имеет
имеет
только простые корни 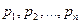 , то оригинал находится по формуле:
, то оригинал находится по формуле:
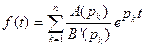 . (3)
. (3)
Теорема 2. Если изображение есть правильная рациональная дробь, то есть  , где
, где  имеет корни
имеет корни 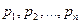 кратности
кратности  , то оригинал находится по формуле:
, то оригинал находится по формуле:
 . (4)
. (4)
Пример 1. Найти оригинал для изображения  .
.
Решение. Знаменатель дроби  имеет простые корни
имеет простые корни 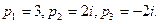 Тогда по формуле (3), учитывая,
Тогда по формуле (3), учитывая,
что  , получим
, получим

Замечание. Если функция  имеет комплексно-сопряженные полюсы
имеет комплексно-сопряженные полюсы  , то легко показать, что и вычеты функции в этих точках будут комплексно-сопряженными, поэтому их сумма равна удвоенной действительной части, то есть
, то легко показать, что и вычеты функции в этих точках будут комплексно-сопряженными, поэтому их сумма равна удвоенной действительной части, то есть
 .
.
С учетом последнего замечания получаем:

Пример 2. Найти оригинал для изображения  .
.
Решение. Корни знаменателя  кратности
кратности  ,
, 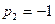 кратности
кратности  . Тогда по формуле (4)
. Тогда по формуле (4)
 ,
,
где 




4) Элементарный метод
Во многих случаях заданное изображение можно преобразовать к такому виду, когда оригинал легко восстановить непосредственно с помощью свойств преобразования Лапласа и таблицы изображений. Для преобразования изображения в этом случае применяют метод разложения рациональной дроби в сумму простейших дробей.
Пример 1. Найти оригинал для изображения  .
.
Решение. Применяя теорему запаздывания, получим

Пример 2. Найти оригинал для изображения 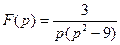 .
.
Решение. Так как 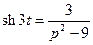 , то применяя теорему об интегрировании оригинала, получим:
, то применяя теорему об интегрировании оригинала, получим:

Пример 3. Найти оригинал для изображения 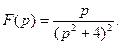
Решение. Можно заметить, что  , и, следовательно, по свойству дифференцирования изображения имеем
, и, следовательно, по свойству дифференцирования изображения имеем 
Пример 4. Найти оригинал по изображению 
Решение. 1 способ. Известно, что  . Тогда по теореме Бореля имеем:
. Тогда по теореме Бореля имеем:  . Найдем свертку
. Найдем свертку

Таким образом, 
2 способ. Разлагаем 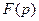 на сумму простейших дробей:
на сумму простейших дробей:

 Отсюда
Отсюда
 Тогда
Тогда

Пример 5. Найти оригинал для изображения

Решение. Выделим в знаменателе полный квадрат и воспользуемся теоремой смещения:

Пример 6. Найти оригинал для изображения

Решение. Выделим в знаменателе полный квадрат и воспользуемся теоремой смещения:

Пример 7. Найти оригинал для изображения

Решение. Найдем вначале оригинал для дроби  . Известно, что
. Известно, что  . Используя теорему смещения, имеем
. Используя теорему смещения, имеем  . Умножение изображения на
. Умножение изображения на  соответствует запаздыванию оригинала, поэтому
соответствует запаздыванию оригинала, поэтому

Упражнения. Найти оригиналы для данных функций 
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
Ответы: 1. 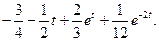 2.
2. 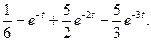
3.  4.
4. 
5. 
6. 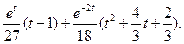 7.
7. 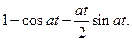
8.  9.
9. 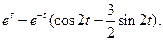
10 
IV. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
1.Решение дифференциальных уравнений и систем дифференциальных уравнений с постоянными коэффициентами
Рассмотрим применение правил и теорем операционного исчисления к решению линейных дифференциальных уравнений с постоянными коэффициентами и их систем
Пусть дано дифференциальное уравнение n-го порядка с постоянными коэффициентами
 . (5)
. (5)
Требуется найти решение уравнения для  при начальных условиях
при начальных условиях
 . (6)
. (6)
Предполагаем, что искомое решение  , его производные и правая часть
, его производные и правая часть  дифференциального уравнения являются оригиналами.
дифференциального уравнения являются оригиналами.
Схема решения дифференциального уравнения.
1. Заменяем искомую функцию, ее производные, входящие в данное дифференциальное уравнение и правую часть их изображениями. В результате получается так называемое операторное уравнение.
2. Решаем операторное уравнение относительно изображения искомой функции.
3. Переходим от изображения искомой функции к оригиналу.
Схема решения систем дифференциальных уравнений такая же.
Пример 1. Найти решение дифференциального уравнения  , если
, если  .
.
Решение. Пусть  , тогда
, тогда


Переходя в уравнении от оригиналов к изображениям, получим операторное уравнение

Отсюда  . Так
. Так
как корни знаменателя  различны, то
различны, то

Ответ: 
Пример 2. Найти решение дифференциального уравнения
 , если
, если 
Решение. Пусть  , тогда
, тогда


 , и по теореме смещения
, и по теореме смещения  .
.
Переходя в уравнении от оригиналов к изображениям, получим операторное уравнение

Отсюда  Разложим изображение
Разложим изображение  на элементарные дроби. Имеем
на элементарные дроби. Имеем

или 

Сравнивая коэффициенты при одинаковых степенях  , находим
, находим 
Тогда  Перейдя к оригиналу,
Перейдя к оригиналу,
пользуясь свойством линейности и теоремой смещения, получаем искомое решение 
Ответ: 
Пример 1. Найти частное решение дифференциального уравнения  ,
,  .
.
Решение. Пусть  ;
; 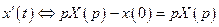 ;
;
 ;
; 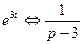 .
.
Запишем операторное уравнение:
 .
.
Откуда
 =
=  =
=
=  .
.
Используя теорему линейности и формулы соответствия, имеем:
 . Пример 2. Найти частное решение дифференциального уравнения
. Пример 2. Найти частное решение дифференциального уравнения  ,
,  .
.
Решение. 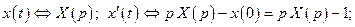





Используя формулы соответствия и теорему линейности, имеем:
 .
.
Пример 3. Найти решение системы дифференциальных уравнений

удовлетворяющее начальным условиям:

Решение. Пусть  ,
,  ,тогда
,тогда

Преобразованная система имеет вид:

Определим  :
:

Найдем по  и
и  оригиналы
оригиналы  и
и  . Пусть
. Пусть 
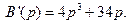 Тогда
Тогда


+  .
.
 ;
; 


Ответ: 
Упражнения.
1. 
Ответ: 
2. 
Ответ: 
3. 
Ответ: 
4. 
Ответ: 
5. 
Ответ: 
6. 
Ответ: 
7. 
Ответ: 
8. 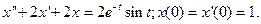
Ответ: 
9. 
Ответ: 
10. 
Ответ: 
11. 
Ответ: 
Упражнения. Найти частные решения дифференциальных уравнений с кусочно-непрерывными правыми частями:
12. 

Ответ: 
13. 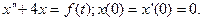

Ответ: 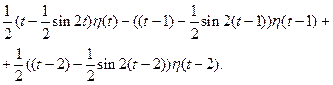
14. 
Ответ:  .
.
15. 
Ответ: 
16. 

Ответ: 
17. 

Ответ: 
Решить системы уравнений:
18. 

Ответ:  .
.
19. 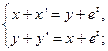

Ответ:  .
.
20. 

Ответ: 
21. 

Ответ:  .
.
22. 

Ответ: 
23. 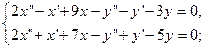

Ответ: 
24. 

Ответ: 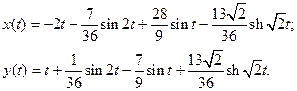
25. 

Ответ: 
26. 

Ответ: 
27. 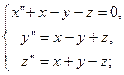

Ответ: 
28. 

Ответ: 
2. Применение формулы Дюамеля для решения дифференциальных уравнений с постоянными коэффициентами.
При решении дифференциальных уравнений иногда удобно использовать формулу Дюамеля. В этом случае не требуется находить изображение правой части.
Пусть требуется найти частное решение дифференциального уравнения
 ;
;  , (7)
, (7)
где  .
.
Рассмотрим вспомогательную задачу
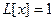 ,
,  . (8)
. (8)
Если  - решение задачи (8), то при помощи интеграла Дюамеля можно найти решение
- решение задачи (8), то при помощи интеграла Дюамеля можно найти решение  задачи (7) с любой правой частью
задачи (7) с любой правой частью  и нулевыми начальными условиями:
и нулевыми начальными условиями:
 или
или  . (9)
. (9)
Замечание. Задачу с ненулевыми начальными условиями заменой искомой функции всегда можно свести к задаче с нулевыми начальными условиями.
Пример. Найти решение уравнения  , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 
Решение. Найдем решение  задачи
задачи 
 ,
,  Составим операторное уравнение
Составим операторное уравнение 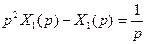 . Отсюда
. Отсюда  , поэтому
, поэтому  По формуле (9) получим:
По формуле (9) получим:

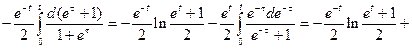


Упражнения. С помощью интеграла Дюамеля найти решения уравнений, удовлетворяющие заданным начальным условиям:
29. 
Ответ: 
30. 
Ответ: 
31. 
Ответ: 
32. 
Ответ: 
33. 
Ответ: 
34. 
Ответ: 
35. 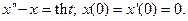
Ответ: 
36. 
Ответ:  .
.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Пискунов Н.С. Дифференциальные и интегральные исчисления. М.: Наука, 2001.Т.2.- 576 с.
2. Романовский П.И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа. - М.: Наука, 1980.-336 с.
3. Краснов М.Л., Киселев А.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. - М.: Наука, 1981.-302 с.
4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. II -М.: Высшая школа, 1986 г.
5.Сборник задач по математике для втузов. Ч.2. Специальные разделы математического анализа. Под редакцией А.В.Ефимова и Б. П. Демидовича. - М.: Наука,1986. -368 с.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для организации самостоятельной работы
по изучению раздела «Операционное исчисление»
курса математический анализ
для студентов специальностей
220300 «Системы автоматизированного
проектирования», 220100 «Вычислительные
машины, комплексы, системы и сети»
дневной формы обучения
Глушко Елена Георгиевна
Дубровская Алевтина Петровна
Провоторова Елена Николаевна
ЛР № 066815 от 25.08.99. Подписано к изданию 20.01.2015.
Уч.-изд.л.3,5. «С»
Издательство
Воронежского государственного технического университета
394026 Воронеж, Московский просп., 14