Геометрический смысл тригонометрических функций

Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан.

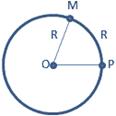
Градусная мера угла в 1 радиан равна:

Так как дуга длиной π R (полуокружность), стягивает центральный угол в 180 °, то дуга длиной R, стягивает угол в π раз меньший, т.е.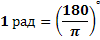

И наоборот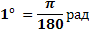

Так как π = 3,14, то 1 рад = 57,3°

Если угол содержит a радиан, то его градусная мера равна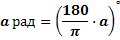

И наоборот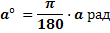

Обычно при обозначении меры угла в радианах наименование «рад» опускают.

Например, 360° = 2π рад, пишут 360° = 2π

Вопрос 2. Вращательное движение

Углы и их измерение

Пусть даны два совпадающих луча 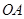- подвижный и 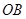- неподвижный. И пусть луч 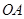поворачиваясь в плоскости вокруг точки 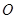, совершит некоторый поворот. Такой поворот, при котором луч 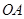впервые опять совпадет с лучом 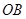, называется полным оборотом.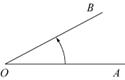

Пусть луч 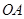совершил некоторый поворот, тогда говорят, что он задает угол 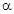, соответствующий этому повороту. Другим определением угла является геометрическая фигура, образованная двумя лучами, исходящими из одной точки 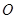, которая называется вершиной угла. Луч 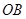носит название начала отсчета и обычно направлен горизонтально вправо.

Градусная мера угла

Поворот, равный 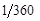полного оборота против часовой стрелки задает угол в один градус. Различают также следующие доли градуса: 1 минута = 1’ = 1/60 градуса; 1 секунда = 1’’ = 1/60 минуты = 1/3600 градуса.

Угол, равный 180^о или половине полного оборота называют развернутым, равный 90^о или четверти полного оборота – прямым.

Радианная мера угла

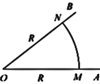Рассмотрим два луча 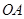- подвижный и 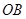- неподвижный. Выберем на них точк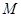и и 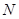, которые в начальный момент времени совпадают. При повороте точка 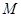будет описывать окружность радиуса 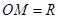. Повернем подвижный луч 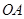так, чтобы точка 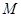прошла расстояние, равное радиусу: 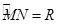, тогда луч 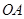составит с лучом 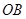угол в один радиан.

Если повернуть подвижный луч 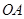так, чтобы точка 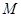прошла расстояние 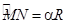, тогда луч 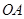составит с лучом 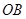угол в 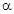радиан.

При совершение полного оборота точка 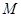проходит расстояние, равное длине окружности 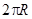, значит полный оборот соответствует углу 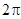радиан.

Радианная мера угла позволяет установить взаимно однозначное соответствие между множеством углов и рядом действительных чисел. Это возможно, поскольку с одной стороны 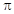- это число, равное 3,14… с другой стороны это угол, соответствующий 180^о. Таким образом, нетрудно установить взаимооднозначное соответствие между углами от 0 до 360^о и действительными числами от 0 до 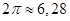. Для того, чтобы понять, как поставить в соответствие углы числам, превышающим 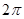, следует вспомнить, что совершив полный оборот подвижный луч возвращается в исходное положение, т.е. любым углам, различающимся на 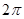или кратное им будет соответствовать одно и то же взаимное положение подвижного или неподвижного лучей. Отрицательные же углы соответствуют повороту подвижного луча против часовой стрелки. Таким образом, любое действительное число представляет собой радианную меру какого-либо угла и наоборот, любому углу можно поставить в соответствие действительное число.

Вопрос 3. Синус, косинус, тангенс и котан­генс числа.

Определения тригонометрическим функциям даются с помощью тригонометрической окружности, под которой понимается окружность единичного радиуса с центром в начале координат.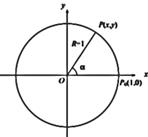

Рассмотрим два радиуса этой окружности: неподвижный 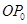(где точка 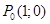) и подвижный 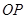(где точка 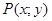). Пусть подвижный радиус образует с неподвижным угол .

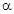Число, равное ординате конца единичного радиуса, образующего угол 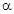с неподвижным радиусом 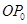, называется синусом угла : .

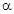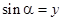Число, равное абсциссе конца единичного радиуса, образующего угол 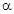с неподвижным радиусом 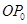, называется косинусом угла : .

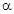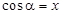Таким образом, точка 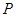, являющаяся концом подвижного радиуса, образующего угол 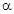, имеет координаты .

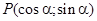Тангенсом угла 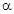называется отношение синуса этого угла к его косинусу: , , .

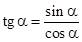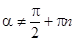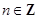Котангенсом угла 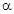называется отношение косинуса этого угла к его синусу: , , .

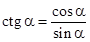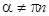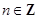Геометрический смысл тригонометрических функций

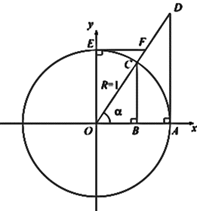Геометрический смысл синуса и косинуса на тригонометрической окружности понятен из определения: это абсцисса и ординат точки пересечения подвижного радиуса, составляющего угол 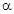с неподвижным радиусом, и тригонометрической окружности. То есть , .

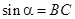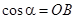Рассмотрим теперь геометрический смысл тангенса и котангенса. Треугольники 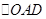подобен 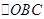по трем углам (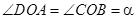, 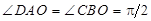), тогда имеет место отношение 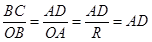. С другой стороны, в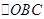 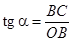, следовательно .

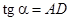Также 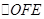подобен 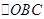по трем углам (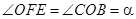, 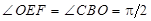), тогда имеет место отношение 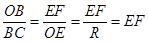. С другой стороны, в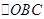 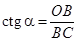, следовательно .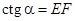