Геометрические элементы зубчатых колес.

Лекция 3 Передаточные механизмы

Вопросы, рассматриваемые на лекции:

1. Назначение и виды передаточных механизмов. Понятие о зубчатых передачах. Геометрические элементы зубчатых колес.

2. Эвольвента и ее свойства.

3. Механизмы, составленные из зубчатых передач

 

Назначение и виды передаточных механизмов.

Понятие о зубчатых передачах.

Геометрические элементы зубчатых колес.

 

Передаточные механизмы служат для передачи и трансформации движения от двигателя (привода) к ведомому (рабочему) механизму. При этом различают передачи трением и передачи зацеплением. В первом случае сообщение движения ведомому элементу осуществляется за счет сил трения, во втором – за счет силового взаимодействия выступов (зубьев) ведущего и ведомого элементов. Как передачи трением, так и зацеплением могут быть с непосредственным контактом или с гибкой связью. Передачи трением: фрикционные и ременные, передачи зацеплением: зубчатые, винтовые, цепные. В большинстве технологических, транспортных и энергетических машин наиболее распространены зубчатые передачи.

Зубчатые передачи (передачи при помощи зубчатых колес) предназначены для передачи вращения между двумя валами с заданным отношением угловых скоростей. Разновидности зубчатых передач по признакам классификации могут быть представлены схемой (табл. 1).

Отношение угловых скоростей пары зубчатых колёс называют передаточным отношением.

i₁₂ = ± ω₁ / ω₂

Если колёса вращаются в одну сторону (внутреннее зацепление), то передаточному отношению приписывают знак (+) в противном случае (внешнее зацепление) - (-). Зубчатые колёса позволяют передавать вращение с постоянным передаточным отношением и с переменным. В первом случае используются круглые зубчатые колеса, а во втором случае - некруглые (овальные эллиптические).

В основе теории зубчатых передач лежит фрикционная передача (передача трением). Хотя фрикционная передача физически в зубчатых колёсах не существует, её можно вообразить в виде двух цилиндров (катков)катящихся друг по другу без скольжения. Эти цилиндры называются начальными цилиндрами, а окружности радиусами r₁ и r₂, которые служат их основаниями, называются начальными окружностями зубчатых колёс.

 

 

Таблица 1 Классификация зубчатых передач

 

 

По положению осей
Плоские	Пространственные
Цилиндрическими колесами с прямыми, наклонными и шевронными зубьями	Цилиндрическими колесами со скрещивающимися осями с круговыми зубьями
С внешним и внутренним зацеплением
Коническими колесами (с прямыми, наклонными или круговыми зубьями)
С пересекающимися осями
Со скрещивающимися осями (гипоидные)
Червячные с цилиндрическим и глобоидным червяком
Продолжение таблицы 1
Зубчато-реечные	Спироидные

 

Начальными окружностями в зубчатых колёсах является та единственная пара окружностей, которые в процессе передачи вращения катятся друг по другу без скольжения. Если колёса должны вращаться в разные стороны, начальные цилиндры получают внешние касания. При вращении в одну сторону цилиндры должны иметь внутренние касания. Точки одной и другой начальной окружности в момент касания должны иметь одинаковые скорости. В частном случае радиус ведомого колеса может быть равен бесконечности, тогда это колесо превращается в рейку, а его начальная окружность в начальную прямую.

В процессе передачи вращения зубья последовательно вступают друг с другом в зацепление, работая как многократная кулачковая передача.

Вычерчивание зубчатого колеса начинается с делительной окружности,диаметра d = 2r, которая является базовой окружностью для определения элементов зуба и их размеров. В стандартной передаче делительная окружность совпадает с начальной окружностью зубчатого колеса.

О₁

r_f1

 

r₁

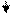
h_a r_a1

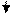
h_f S e r_f2

r₂

 

 

r_a2

O₂

 

Рис. 1 Геометрические элементы зубчатого зацепления

Делительная окружность делит зубья по высоте на две части: головку и ножку. Пространство между двумя зубьями называется впадиной. Зубья ограничены по высоте двумя окружностями:

а) окружностью вершин зубьев диаметром d_a=2r_a

б) окружностью впадин диаметром d_f=2r_f

Высота зуба равна: h=h_a+h_f, где h_a - высота головки зуба, h_f -высота ножки зуба.

Толщина зуба S - дуга делительной окружности, вмещающая один зуб. Ширина впадины e - дуга делительной окружности, вмещающая одну впадину.

Шаг зубьев Р - дуга делительной окружности, вмещающая один зуб и одну впадину: P = S + e.

Шаг зубьев Р можно определить также как расстояние по делительной окружности между одноимёнными точками двух соседних зубьев.

В паре зубчатых колес малое колесо называют шестерней, а большое -колесом. Если колеса имеют одинаковый делительный диаметр, то шестерней является ведущее колесо.

Шаги зацепления двух сопряжённых колёс, измеренные по начальным окружностям колёс должны быть одинаковыми, т.е.

2 ₁ = Pz₁ и 2 ₂ = Pz₂

Отсюда следует, что =

Следовательно, передаточное отношение в паре зубчатых колес может определяться несколькими методами:

 

Знак (–) относится к внешнему зацеплению, а знак (+) к внутреннему зацеплению.

z ₁ и z₂- числа зубьев колёс.

Для любого зубчатого колеса справедливо: 2 = Pz,

отсюда d = 2r = z.

По конструктивным и технологическим соображениям диаметры зубчатых колёс должны выражаться рациональными числами. Для этого шаг зубьев Р должен быть числом иррациональным. Пользоваться им практически неудобно. Поэтому шаг зубьев принято характеризовать рациональной величиной:

m = Р/π, (1)

которая называется модулем зубчатого колеса и измеряется в мм. С учётом этого получим выражение для делительного диаметра зубчатого колеса d = mz.

Модуль определяет все размеры зубчатого колеса и зуборезного инструмента. Его величина находится из условий прочности и износостойкости зуба.

Чтобы не иметь на заводах больших комплектов зуборезных инструментов, значения модуля и размеры зубьев стандартизированы.

ГОСТом предусмотрены два типа зубьев:

1-Нормальной высоты h_a=m и h_f=1.25m

2-Укороченные зубья h_a=0,8m и h_f=1.1m

Диаметры окружностей вершин зубьев и окружностей впадин определяются следующими соотношениями.

Зубья нормальной высоты: d_a=m(z+2), d_f=m(z-2.5)

Делительное межосевое расстояние:

Внешнее зацепление: a= ( + )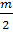

Внутреннее зацепление: a= 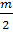( - ).