В электротехнических расчетах встречается широкий спектр задач ограниченной сложности, для решения которых можно использовать универсальные средства. К таким задачам относятся следующие:
1) подготовка научно-технических документов, содержащих текст и формулы,
записанные в привычной для специалистов форме;
2) вычисление результатов математических операций, в которых частвуют числовые константы, переменные и размерные физические величины;
3) операции с векторами и матрицами;
4) решение уравнений и систем уравнений (неравенств);
5) статистические расчеты и анализ данных;
6) построение двумерных и трехмерных графиков;
7) тождественные преобразования выражений (в том числе упрощение),
аналитическое решение уравнений и систем;
8) дифференцирование и интегрирование, аналитическое и численное;
9) решение дифференциальных уравнений;
10) проведение серий расчетов с разными значениями начальных условий и других параметров.
Научно-технические документы, содержащие электротехнические расчеты, обычно содержат формулы, результаты расчетов в виде таблиц данных или графиков, текстовые комментарии или описания, другие иллюстрации. В программе MathCad [1, 2, 3] им соответствуют два вида объектов: формулы и текстовые блоки. Формулы вычисляются с использованием числовых констант, переменных, функций (стандартных и определенных пользователем), а также общепринятых обозначений математических операций. Введенные в документ MathCad формулы автоматически приводятся к стандартной научно-технической форме записи.
Графики, которые автоматически строятся на основе результатов расчетов, также рассматриваются как формулы. Комментарии, описания и иллюстрации размещаются в текстовых блоках, которые игнорируются при проведении расчетов.
|
|
Чтобы буквенные обозначения можно было использовать при расчетах по формулам, этим обозначениям должны быть сопоставлены числовые значения. В программе MathCad буквенные обозначения рассматриваются как переменные, и их значения задаются при помощи оператора присваивания (вводится символом «:»). Таким же образом можно задать числовые последовательности, аналитически определенные функции, матрицы и векторы.
Если все значения переменных известны, то для вычисления числового
значения выражения (скалярного, векторного или матричного) надо подставить все числовые значения и произвести все заданные действия. В программе MathCad для этого применяют оператор вычисления (вводится символом «=»). В ходе вычисления автоматически используются значения переменных и определения функций, заданные в документе ранее. Удобно задать значения известных параметров, провести вычисления с использованием аналитических формул, результат присвоить некоторой переменной, а затем использовать оператор вычисления для вывода значения этой переменной. Например:
a:= 6.4
b:= 2
S:= a⋅b
S= 12.8.
Изменение значения любой переменной, коррекция любой формулы, означает, что все расчеты, зависящие от этой величины, необходимо проделать заново. Такая необходимость возникает при выборе подходящих значений параметров или условий, поиске оптимального варианта, исследовании зависимости результата от начальных условий. Электронный документ, подготовленный в программе MathCad, готов к подобной ситуации. При изменении какой-либо формулы программа автоматически производит необходимые вычисления, обновляя изменившиеся значения и графики. Например, если документ содержит
|
|
формулы n:= 9; √n =3, то, изменив значение переменной n, мы сразу же увидим, что изменился и результат расчета: n:= 25; √n =5.
При проведении расчетов с использованием реальных физических величин учитывают их размерность. Чтобы расчет был корректен, все данные должны быть приведены в одну систему единиц — в этом случае результат расчетов получится в этой же системе. Здесь скрывается характерный источник ошибок при расчетах вручную. В программе MathCad единицы измерения (в любой системе) присоединяют к значению величины с помощью знака умножения. Данные автоматически преобразуются в одну и ту же систему единиц (по
умолчанию СИ) и обрабатываются в этом виде. Размерный результат выдается вместе с полученной единицей измерения. Например:
v:= 100⋅kph t:= 0.5⋅yr (kph — километры в час, yr — годы),
s:=v⋅t s= 4.383⋅108m (результат получен в метрах).
При работе с матрицами приходится применять такие операции, как сложение матриц, умножение, транспонирование. Часто возникает необходимость в обращении матриц и в декомпозиции (разложении в произведение матриц специального вида). Программа MathCad позволяет выполнить все эти операции с помощью стандартных обозначений математических операторов (сложение, умножение) или встроенных функций.
Уравнения и системы уравнений, возникающие в практических задачах,
обычно можно решить только численно. Методы численного решения
|
|
реализованы и в программе MathCad. Блок уравнений и неравенств, требующих решения, записывается после ключевого слова ‘given’ (дано). При записи уравнений используется знак логического равенства (комбинация клавиш ‘CTRL+=’). Значения переменных, удовлетворяющие системе уравнений и неравенств, находятся с помощью стандартной функции ‘find’. Например:
x:= 0 y:= 0
given
х+у =1
x2+y2=4
find(x,y)= 
При обработке результатов экспериментов часто встречаются задачи
статистического анализа серий данных. Для такого рода задач программа MathCad предоставляет средства интерполяции данных, предсказания дальнейшего поведения функции, а также построения функций заданного вида, наилучшим образом соответствующих имеющемуся набору данных. При статистическом анализе можно также использовать стандартные функции распределения вероятности и генераторы случайных величин с заданным распределением.
При аналитических вычислениях результат получают в нечисловой форме в результате тождественных преобразований выражений. Простейшие преобразования — это раскрытие скобок, приведение подобных членов, применение тригонометрических тождеств.
Более сложные преобразования позволяют находить аналитические решения некоторых уравнений и систем. Для такого рода вычислений в программе MathCad используют оператор аналитического вычисления (клавиатурная комбинация ‘CTRL+’), а также команды меню Symbolics (Аналитические вычисления). Переменные при аналитических вычислениях рассматриваются как неопределенные параметры. Результат можно использовать для анализа решения при различных значениях этих переменных. При аналитическом решении уравнений и систем за одну операцию можно найти все существующие решения.
Дифференцирование и интегрирование заданных функций вручную — обычно несложная, но трудоемкая операция. В программе MathCad для вычисления производной, а также неопределенных и определенных интегралов могут использоваться символические вычисления с помощью меню Symbolics — Variable (Аналитические вычисления — Переменная). Если функция не задана аналитически или не позволяет получить первообразную в виде формулы, имеется возможность численного дифференцирования и численного расчета определенных интегралов.
Численные методы используют и для решения дифференциальных уравнений. С помощью программы MathCad можно решать уравнения и системы уравнений первого порядка с заданными начальными условиями. Уравнение более высокого порядка надо сначала преобразовать в систему уравнений первого порядка.
Анализ задач в электротехнике сводится к решению систем уравнений (линейных, нелинейных, дифференциальных) составленных по законам Кирхгофа. Основной недостаток уравнений Кирхгофа заключается атом,что необходимо решать системы уравнений большого порядка. Традиционно системы уравнений записанных по законам Кирхгофа сводили к уравнения меньшего порядка на основании методов, например: метод контурных токов, метод узловых напряжений, метод эквивалентных преобразований и т.д.
Но если использовать пакеты прикладных программ (Mathcad, MatLab и др.), можно анализ электротехнических задач свети к решению уравнений записанных по законам Кирхгофа, как в численном так и символьном виде.
Далее представлены примеры расчетных решений.
2.1. Электрическая цепь постоянного тока с одним источником питания
При расчете электрических цепей постоянного тока с одним источником питания часто необходимо проводить вычисления, связанные с нахождением эквивалентного сопротивления цепи, с определением токов во всех ветвях цепи и напряжений на источнике и на каждом приемнике отдельно.
Рассмотрим пример расчета электрической цепи, представленной на рис. 2 с помощью программы MathCad. Приемы работы в программе MathCad, используемые в данной примере, рассмотрены в главе 1.1.
Из условия задачи известны величина ЭДС аккумуляторной батареи E, ее внутреннее сопротивление R0 и сопротивления приемников R1, R2, R3. На первом этапе расчета определяем эквивалентное сопротивление цепи Rc, воспользовавшись правилами последовательного и параллельного соединения пассивных элементов цепи. Затем, используя законы Ома для участка цепи, а также закон Кирхгофа для замкнутого контура, рассчитываем токи во всех ветвях цепи I, I1, I2 и напряжения на отдельных участках U, U12, U3. Расчет представлен на рис. 3.
Значения исходных величин могут быть изменены, представленные формулы могут быть скорректированы в зависимости от характера электрической цепи, однако возможности программы MathCad позволяют автоматически производить необходимые вычисления, обновляя изменившиеся значения.

Рис. 2. Электрическая цепь с одним источником питания

Рис. 3. Расчет электрической цепи с одним источником
2.2. Расчет однофазных цепей синусоидального тока
Существует несколько методов расчета однофазных цепей синусоидального тока, например: графоаналитический, комплексный (символический) и другие. При проведении электротехнических расчетов разветвленных и неразветвленных цепей переменного тока удобно использовать все известные методы анализа цепей постоянного тока. В этом случае применяется комплексный метод расчета.
С помощью средств программы MathCad возможно производить расчеты, используя величины, выраженные в комплексном виде. Особенностью формы записи комплексных чисел в программе MathCad является следующее: при вводе комплексных чисел нельзя использовать i или j сами по себе, необходимо всегда печатать Ii или Ij. В MathCad существуют следующие специальные функции и операторы для работы с комплексными числами:
Re (z) — вещественная часть;
Im(z) — мнимая часть;
arg(z) — угол в комплексной плоскости между вещественной осью и z.
Возвращает результат между –π и π радиан;
|z| — модуль z. Чтобы записать модуль от выражения, заключите его в выделяющую рамку и нажмите клавишу с вертикальной полосой |.
_
z — число, комплексно сопряженное к z. Чтобы применить к выражению оператор сопряжения, выделите выражение, затем нажмите двойную кавычку (“).
На рис. 7 представлен пример перевода из алгебраической формы записи комплексного числа в показательную форму и обратно, что необходимо при выполнении электротехнических расчетов цепей переменного тока.
Приведем пример расчета сложной цепи переменного тока, представленной на рис. 8. Исходными данными для задачи являются величины сопротивлений и напряжения на входе схемы. Расчет цепи произведем поэтапно. Сначала рассчитаем проводимости параллельного участка цепи, затем полное сопротивление цепи. Этот расчет представлен на рис. 9.

Рис. 7. Представление комплексного числа в показательной и алгебраической форме

Рис. 8. Схема электрической цепи синусоидального тока

Рис. 9. Расчет проводимостей и сопротивлений цепи
Воспользовавшись полученными данными, определим все токи и напряжения в цепи, используя законы Ома и Кирхгофа для цепей переменного тока. Расчет токов и напряжений представлен на рис. 10.
На следующем этапе расчета цепи определим активные, реактивные и полные мощности источника и всех приемников, произведем расчет баланса мощностей. Данные расчета показаны на рис. 11. Сравниваем значения Sс (полная мощность источника синусоидального тока) и S (полная мощность всех приемников цепи) и убеждаемся в том, что баланс мощностей «сошелся». Это означает, что задача решена верно.

Рис. 10. Расчет токов и напряжений

Рис. 11. Баланс мощностей
На последнем этапе расчета проверяем выполнение первого и второго законов Кирхгофа для цепей синусоидального тока. Этот этап расчета представлен на рис. 12. На рис. 12 величина I — это ток во всей цепи. Сравниваем ее с Iл и убеждаемся, первый закон Кирхгофа для узла цепи синусоидального тока выполняется. Подтверждение второго закона Кирхгофа наблюдаем при сравнении двух величин: U — напряжение источника тока и Uс — напряжение сети.

Рис. 12. Расчет токов и напряжений с помощью первого и второго законов Кирхгофа для цепей синусоидального тока
Таким образом, с помощью средств программы MathCad произведен расчет сложной цепи синусоидального тока.
2.3. Машины постоянного тока
При расчете машин постоянного тока часто необходимо рассчитывать и строить механические характеристики машины. Возможность построения различных графиков является одной из функции программы MathCad. Правила построения графиков в MathCad описаны в главе 1.2.7.
На примере двигателя постоянного тока параллельного возбуждения построим естественную и искусственные механические характеристики в одной системе координат. Электрическая схема двигателя показана на рис. 13. Двигатель постоянного тока параллельного возбуждения с номинальным напряжением 220 В имеет номинальную мощность Рн, номинальную частоту вращения nн, номинальный КПД ηн и сопротивления обмоток якоря Rя, возбуждения — Rв.
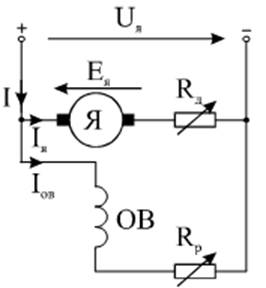
Рис. 13. Электрическая схема двигателя постоянного тока параллельного возбуждения
Для построения механических характеристик рассчитываем параметры двигателя в номинальном режиме. Расчеты представлены на рис. 14. После этого, указав диапазон изменения момента, записываем уравнения стественной n=f(M) и искусственных n1=f(M) (в якорную цепь добавлен пусковой реостат Rп для ограничения пускового тока до 2Iян), n2=f(M) (регулирование частоты вращения двигателя путем ослабления поля за счет введения резистора в цепь возбуждения до 0,7Фн), n3=f(M) (регулирование частоты вращения двигателя путем понижения на 15% подведенного к обмотке якоря напряжения при номинальной нагрузке) характеристик, как показано на рис. 15. На рис. 16 представлено семейство механических характеристик для двигателя постоянного тока араллельного возбуждения, построенные средствами программы MathCad.

Рис. 14. Расчет параметров двигателя в номинальном режиме

Рис. 15. Уравнения механических характеристик двигателя постоянного тока параллельного возбуждения

Рис. 16. Семейство механических характеристик двигателя постоянного тока