При решении тригонометрических неравенств учащиеся часто допускают ошибки в окончательном отборе решений.
Опишем методический подход к заключительному этапу решения тригонометрического неравенства, который удобно разъяснять учащимся с помощью специально составленного алгоритмического предписания.
1. Привести неравенство к такому виду, чтобы в одной его части (например, в правой) был ноль. T (x) <> 0
2. Определить нули и точки разрыва функции Т (х), стоящей в левой части неравенства.
3. Расставить на единичной окружности точки, являющиеся представителями всех найденных чисел.
4. Выбрать произвольное число ц (значение аргумента функции, стоящей в любой части неравенства), не совпадающей ни с одним из ранее полученных чисел.
5. Провести луч Ох' под углом ц к координатному лучу Ох.
6. На луче Ох' получить контрольную точку xк. Для этого подставить число ц в левую часть неравенства определить знак получившегося выражения.
Если выражение больше нуля, то xk-это произвольная точка луча ox, лежащая вне единичной окружности.
Иначе xk - это произвольная точка луча ox внутри единичной окружности.
7. Начиная с точки xk провести плавную линию так, чтобы она пересекала единичную окружность во всех отличительных точках последовательно в порядке обхода единичной окружности против часовой стрелки. Пройдя все точки линия должна вернуться в точку xk.
8. выбрать нужные участки, которые образовала проведенная линия. Для этого: если выражение, стоящее в левой части неравенства больше нуля, то выбрать участки, лежащие вне единичной окружности. иначе- выбрать те участки фигуры, лежащие внутри единичной окружности.
9. отметить стрелками в положительном направлении те дуги единичной окружности, которые принадлежат выбранным участкам. Эти дуги соответствуют множеству решений неравенства.
Проиллюстрируем описанный метод.
Пример 19решить неравенство
 ц
ц
Приведем левую часть неравенства к виду
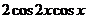 и рассмотрим уравнение
и рассмотрим уравнение
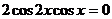 , которое равносильно совокупности уравнений
, которое равносильно совокупности уравнений
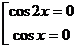
Первое из уравнений этой совокупности дает Iсерию значений x:
xI =р/4+ рз/2, второе – II серию: xII = р/2+ рз.
Заполним теперь единичную окружность соответствующими точками. Для I серии достаточно взять з=0,1,2,3. Тогда значение xI соответственно равны р/4, 3р/4, 5р/4, 7р/4 (при остальных значениях з точки будут повторяться). Значения из серии xII на единичной окружности можно представить точками рз/2 и 3р/2, которые получены при з=0 и з=1.
Выберем теперь контрольную точку, положив ц=0.
Тогда cos3 * 0 + cos0 = 2 > 0.
Значит, в данном случае луч Ox совпадает с координатным лучом Ox (угол между ними равен 0). Выберем на луче Ox произвольную точку xk, находящуюся вне единичной окружности.
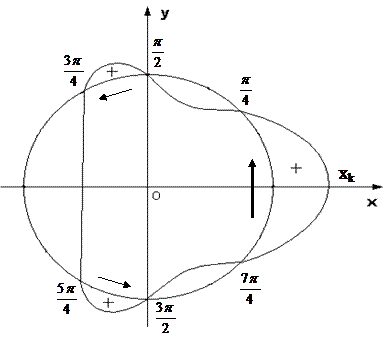
Соединяем точку xk со всеми отмеченными точками на единичной окружности так, как показано на рисунке.
Решению исходного неравенства соответствуют дуги единичной окружности в тех областях, которые отмечены на рисунке знаком «+». При записи окончательного ответа следует иметь ввиду, что в одной из областей(она показана двойной стрелкой) нарушается переход от меньших значений х к большим. В таком случае следует к меньшему значению(р/4) прибавить 2р или от большего значения (7р/4) отнять 2р.
 |
Итак, окончательное решение можно записать в виде совокупности промежутков:
 .
.
Заметим, что если волнообразную линию знаков после обхода его всех отмеченных на единичной окружности точек не удается вернуть в точку xk, не пересекая окружность в «незаконном» месте, то это означает, что в решении ошибка, а именно пропущено нечетное количество корней.
Приведенный пример имеет одну особенность. Серии xI и xII дают на единичной окружности несовпадающие точки. Если же некоторые точки разных серий совпадают то будем называть их кратными. Волнообразная линия, идущая от точки xк, после встречи с точкой нечетной кратности обязана перейти в иную область. Точка четной кратности не дает линии перейти в иную область.
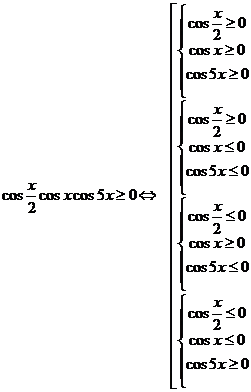
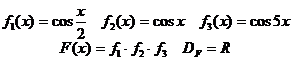
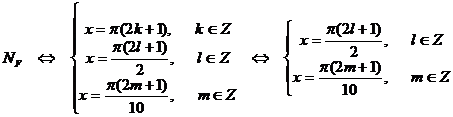
учитывая, что каждая из функций f1, f2, f3 меняем знак при переходе через точки, в которых она обращается она в нуль, что F(0) > 0 и что в точках: 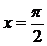 и
и 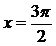 функции f2 и f3 обращаются в нуль одновременно, получаем следующее распределение знаков F(x) на отрезке [0; 2 р ], так как функция четная и периодическая с периодом 4 р, то мы получаем
функции f2 и f3 обращаются в нуль одновременно, получаем следующее распределение знаков F(x) на отрезке [0; 2 р ], так как функция четная и периодическая с периодом 4 р, то мы получаем
F(x)  0 <=>
0 <=> 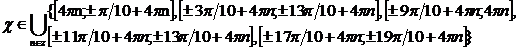
Так же это неравенство можно решить с помощью интервалов на тригонометрической окружности.
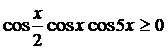
Рассмотрим совокупность уравнений:
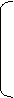
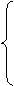
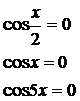 отсюда
отсюда 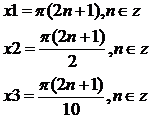
На единичной окружности значения серии х1 представлены одной точкой р.
х2 дает 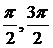
х3 - 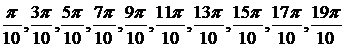
Нанесем все эти точки на единичную окружность, указав в скобках их кратность.
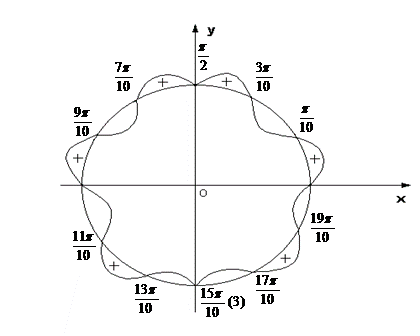
Т.к. F(0)>0, то от точки «0» ведем волнообразную линию ко всем отмеченным точкам.
Т.к. F(x) – нечетная и периодическая с периодом 4р, то:
F(x)  0 <=>
0 <=> 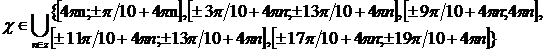
Графический метод
Графический метод можно считать представителем стандартного метода решений неравенств, однако в школьной программе он занимает весьма скромное положение, на практике он вообще фактически не изучается. А ведь его по праву можно назвать наиболее эффективным в силу наглядности.
Предположим, на пример, что решается неравенство f(x)  g(x), причем графики функций y=f(x) и y=g(x) имеют следующий вид:
g(x), причем графики функций y=f(x) и y=g(x) имеют следующий вид:
 |
Тогда очевидно, решение нашло неравенство – есть интеграл [x1, x2], т.е. участок, где график функции y = g(x) лежит «не выше» графика функции y = f(x).
В общем случае, пусть дано неравенство F(x) *, где знак * есть  , >, < или
, >, < или 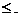
Если после эментарных преобразований неравенство F(x) * приобретает вид f(x) * g(x), функции y = f(x) и y = g(x) легко представлены в графическом виде, то в этом случае для решения неравенства F(x) * 0 можно использовать графический метод.
Пример:
20x2 - 7x +12 < | x - 4 |
y = f(x) = x2 - 7x +12
y = g(x) = | x - 4 |
Строим графики этих функций.
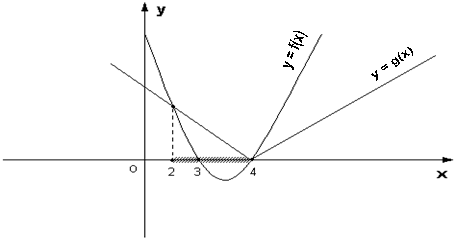
Находим точки их пересечения:
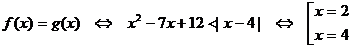
после проверки 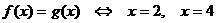
Запишем ответ нашего неравенства: 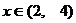
Ответ: 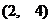
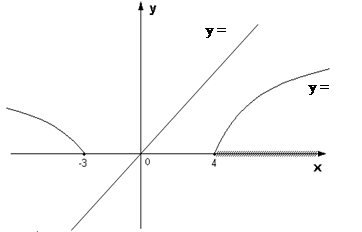
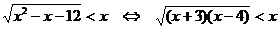
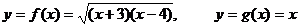
Строим график итих функций:
Из рисунка наглядно видно, что решением неравенства является интервал 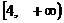
Нестандартные методы
Существуют два типа нестандартных задач: задачи нестандартные по содержанию и задачи решаемые нестандартными методами.
I. Неравенства решаемые нестандартными методами
На практике встречаются неравенства, решить которые можно обычным шаблонным методом, проводя громоздкие выкладки, а можно, проявляя некоторую изобретательность придти к решению интересным и красивым путем, при том гораздо быстрее.
Один из таких путей использование монотонности функции при решении неравенств.
Проиллюстрируем эту идею на примере:
22. Решить неравенство 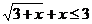
Запишем его в виде: 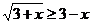
Стандартный путь: метод с.с.
Нестандартный способ: функция расположенная в левой части, монотонно возрастает, а правой – убывает. Из очевидных графических соображений следует, что уравнение 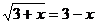 имеет не более одного решения, причем если х0 – решение этого уравнения, то при -
имеет не более одного решения, причем если х0 – решение этого уравнения, то при - 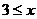 <x0 будет
<x0 будет 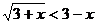 , а решением исходного неравенства будет
, а решением исходного неравенства будет 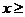 х0 .
х0 .
Значение х0 легко подбирается: х0 =1
Ответ: 
Данное неравенство 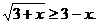 можно решить еще одним методом, который также отнесем к нестандартным методам: метод замены неизвестного.
можно решить еще одним методом, который также отнесем к нестандартным методам: метод замены неизвестного.
Расставим неравенство 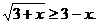 и сделаем замену
и сделаем замену 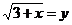 , тогда
, тогда 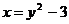 в результате чего исходное неравенство примет вид
в результате чего исходное неравенство примет вид 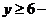 y2 . получим квадратное неравенство y2+y-6
y2 . получим квадратное неравенство y2+y-6 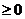 решая данное неравенство получаем, что
решая данное неравенство получаем, что 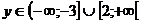 т.к.
т.к.  в итоге получаем
в итоге получаем 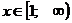
Ответ: 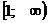
Рассмотрим еще один нестандартный метод
23. 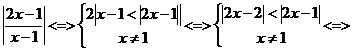
<=> 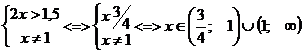
решить такое неравенство – это значит на числовой прямой отыскать точки 2x расстояние от которых до 2 меньше расстояния до 1
 точка 1,5 середина отрезка
точка 1,5 середина отрезка 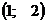
Ответ: 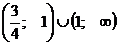
2. Рассмотрим нестандартные по формулировке задачи, связанные с неравенствами.
Для того чтобы понять, какие именно задачи считать нестандартными по формулировке, достаточно просто посмотреть на условие задачи. С первого взгляда ясно, что обычные преобразования, какие-либо алгебраические или тригонометрические формулы не приведут к цели, если на ряду с ними не применить рассуждения иного рода.
Примеры:
24. Найти все целые значения x, удовлетворяющие неравенству.
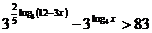
Решение: Область определения неравенства  .
.
Значит нам достаточно рассмотреть три значения x:1;2;3
Если х=1, то 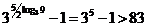
Если х=2, то 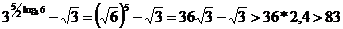
Если х=3, то 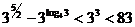
Ответ: 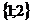
25. найти все целые х, удовлетворяющие неравенству
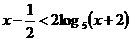
Решение: рассмотрим функцию
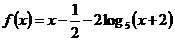
Докажем, что начиная с некоторого х, 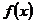 возрастает. Это можно сделать обычным путем, оценивая производную. Мы сделаем иначе. Нам достаточно доказать возрастание функции для целых х, т.е. что
возрастает. Это можно сделать обычным путем, оценивая производную. Мы сделаем иначе. Нам достаточно доказать возрастание функции для целых х, т.е. что
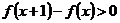
имеем 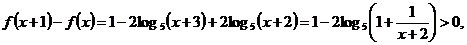
 ,
, 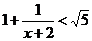
Последнее неравенство выполняется при 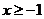 , т.е. для всех допустимых целых х.
, т.е. для всех допустимых целых х.
Нам осталось найти наибольшее целое, для которого 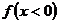 или наименьшее, что
или наименьшее, что 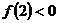 ;
; 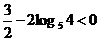
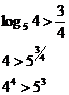
Далее. 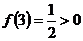
Ответ: 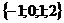
К рассматриваемому типу неравенств можно отнести неравенства, решение которых зависит от параметра
26. Найти все значения параметра а, при которых существует единственное значение х, при котором выполняется неравенство.
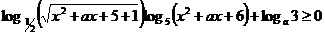
Решение: обозначим 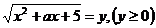 и перейдем к обоснованию 5.
и перейдем к обоснованию 5.
Получим 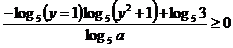
Функция от y, расположенная в числителе монотонно убывает.
Нетрудно подобрать значение y, при котором она обращается в нуль: y =2
Если 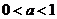 ,то решением неравенства относительно у будет
,то решением неравенства относительно у будет 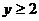 , а следовательно исходное неравенство не может иметь единственное решение.
, а следовательно исходное неравенство не может иметь единственное решение.
(неравенство 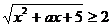 ) при любом а бесконечно много решений).
) при любом а бесконечно много решений).
Значит а >1 и решение относительно у будет 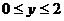
Возвращаясь к х, будем иметь: 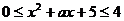 .
.
Для того, чтобы существовало единственное значение х, удовлетворяющее последним неравенствам, необходимо и достаточно, чтобы наименьшее значение квадратного трехчлена 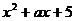 равнялось бы 4, т.е.
равнялось бы 4, т.е. 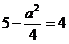
Ответ: а =2
27. найти все значения р, при каждом из которых множество решений неравенства 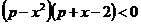 .
.
Решением последнего неравенства при данном х относительно р, состоит из двух лучей, исключается внутренняя часть отрезка с концами 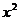 и – х +2. Но если х меняется от –1 до 1, то х 2 меняется от0 до3, а при
и – х +2. Но если х меняется от –1 до 1, то х 2 меняется от0 до3, а при 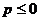 и при
и при 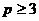 данное условие выполняется. (пусть
данное условие выполняется. (пусть 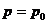 и
и 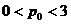 . Если
. Если 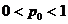 , то возьмем
, то возьмем 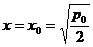 . При этих
. При этих 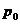 и
и 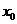 будет
будет 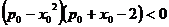 )
)
К не стандартным методам, можно также отнести и решение неравенств с параметрами графическим методом.
Следует выделить две разновидности графического метода решения неравенств с параметрами:
1). Изображение на плоскости (х,а), где х - неизвестное, а - параметр.
2). На плоскости (х,у) рассматривается семейство кривых зависящих от параметра.
Рассмотрим примеры:
28. При любом значении параметра а решить неравенство.
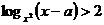
Решение: Рассмотрим плоскость (х; a) и изобразим на ней множество точек, координаты которых удовлетворяют неравенству. Сначала изобразим область, для точек которой имеет смысл 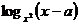 . это будет плоскость
. это будет плоскость 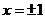 .
.
Вне полосы, ограниченной прямыми 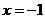 и
и 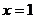 , будет
, будет 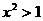 , и, следовательно, после потенцирования неравенства получим
, и, следовательно, после потенцирования неравенства получим 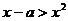 ,
, 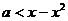
Последнему неравенству соответствует область под параболой 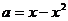 (при этом
(при этом 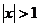 ).
).
Внутри полосы 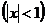 будет
будет 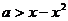
Заметим, что парабола 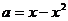 касается прямой
касается прямой 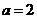 . Ось а точками
. Ось а точками 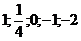 разбита на шесть участков.
разбита на шесть участков.
На рисунке область 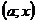 для точек которой
для точек которой 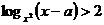 заштрихована.
заштрихована.
неравенство решение системосовокупность тригонометрический графический
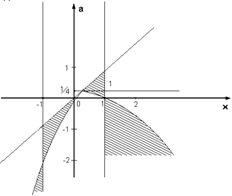
На каждом из участков по оси а выписываем решение нашего неравенства. Для этого берем а на соответствующем участке, проводим горизонтальную прямую находим значение х, соответствующие отрезков этой прямой, попавших в заштрихованную зону.
Например, если 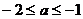 , то получим два отрезка концы первого:
, то получим два отрезка концы первого: 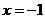 и
и 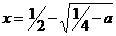 (меньший корень уравнения
(меньший корень уравнения 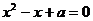 ), второго:
), второго: 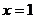 и
и 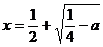
Таким образом ответ:
1. если 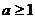 ,
, 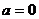 - решений нет
- решений нет
2. если 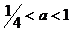 , то
, то 
3. если 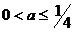 , то
, то 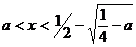 и
и 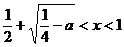
4. 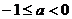 , то
, то 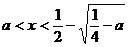 и
и 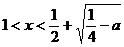
5. если 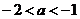 , то
, то 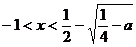 и
и 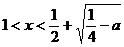
6. если 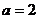 , то
, то 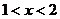
7. если 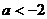 , то
, то 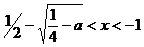 и
и 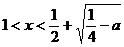
Размещено на Allbest.ru