В г. Коломне Московской области
_______________________________________________________________________
КАФЕДРА СТРОИТЕЛЬНОГО ПРОИЗВОДСТВА
Н.Н. Адамушко
МАТЕРИАЛЫ
Расчетно-графической работы
По математике
Векторная алгебра
Аналитическая геометрия
Для студентов 1-го курса (1 семестр) специальностей
КТО, 13.03.03-ЭМС, 08.03.01-С
Очная форма обучения
МАМИ Коломна
УДК 517.5/.8
ББК 22.161.5
А28
Рецензент:
кандидат физ.-мат. наук, доцент кафедры строительного производства МАМИ
Балабан Е.И.
Адамушко Н.Н.
Материалырасчетно-графической работы по математике
Векторная алгебра
Аналитическая геометрия
для студентов 1го курса (1 семестр) специальностей
15.03.05-КТО, 13.03.03-ЭМС, 08.03.01-С – МАМИ Коломна, 2015, 37 с.
Учебно-методическое пособие содержит задания (30 вариантов) и требования к выполнению РГР математике по курсу «Векторная алгебра. Аналитическая геометрия ». Предназначено для студентов 1го курса (1 семестр) специальностей 15.03.05-КТО, 13.03.03-ЭМС, 08.03.01-С
Рассмотрено на заседании
кафедры строительного производства
24.10.2012г., протокол №2
Содержание
1. Требования к выполнению расчетно-графических работ...........................4
2. Правила выполнения расчетно-графических работ………………………..4
3. Требования к оформлению расчетно-графической работы.……………...4
4. Срок представления расчетно-графической работы …...……………...…..4
5. Образец оформления титульного листа…………………………………….5
6. Содержание расчетно-графической работы ………………………………..6
Требования к выполнению расчетно-графической работы
1. Каждый студент 1-го курса в 1-м семестре должен выполнить две расчетно-графические работы по математике.
|
|
2. Задания выбираются по номерам списка учебной группы.
3. Требования к оформлению работы и титульного листа приведены далее.
4. Выполненные РГР должны быть представлены до указанного срока.
Правила выполнения расчетно-графической работы
1. При выполнении контрольной расчетно-графической работы необходимо строго придерживаться указанных ниже правил. Работа, выполненная без соблюдения этих правил не зачитывается и возвращается для переработки.
2. Контрольная работа должна быть выполнена в отдельной тетради в клетку синими или черными чернилами.
3. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, номер зачетной книжки, номер контрольной работы, название дисциплины. В конце работы следует поставить дату ее выполнения и расписаться.
4. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту.
5. Решения задач следует располагать в порядке номеров, указанных в задании, сохраняя номера задач.
6. Перед решением каждой задачи надо полностью написать ее условие. В том случае, если несколько задач, из которых студент выбирает задачу своего варианта, имеют общую формулировку, следует, переписывая условия задачи, заменить общие данные конкретными, взятыми из соответствующего номера.
7. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая четкие и соразмерные необходимые чертежи.
Требования к оформлению работы
Формат: А4. WORD 2003: кейгль 14, «times new roman», поля: левое-30 мм, правое-10 мм, верх и низ-20 мм. Межстрочный интервал: полуторный. Формулы: Equation или Math Type Графика: любой редактор, импортируемый в WORD.
|
|
Объём: без ограничений.
Срок представления РГР
РГР должна быть сдана до 30 октября (29 октября последний день)
| МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Коломенский институт (филиал) ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ МАШИНОСТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ(МАМИ)» |
В г. Коломне Московской области
_______________________________________________________________________
КАФЕДРА СТРОИТЕЛЬНОГО ПРОИЗВОДСТВА
РГР
Название темы
Автор: студент группы
№ группы
Фамилия И.О.
№ зачетной книжки
Рецензент: доцент(профессор)
Фамилия И.О.
Дата представления
Коломна-2015
Расчетно-графическая работа №1
«Векторная алгебра»
«Аналитическая геометрия»
состав расчетно-графической работы № 1 входят восемь задач по темам, изучаемым в первой половине 1 семестра: исследование уравнения кривой, различные уравнения прямой на плоскости, различные уравнения плоскости, взаимное расположение прямой и плоскости, поверхности второго порядка.
Вариант 1
1. Упростить уравнение и построить кривую.
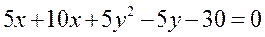
2. Даны 3 вектора: 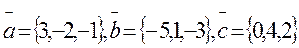 Найти:
Найти:
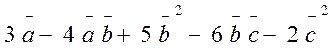
3. Найти 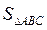 , если его вершины А(4,2,5), В(0,7,2), С(0,2,7).
, если его вершины А(4,2,5), В(0,7,2), С(0,2,7).
4. Дана прямая x + 2y – 4 = 0 и т. А(5,7). Найти проекцию т.А на прямую.
5. Вычислить угол между прямыми:
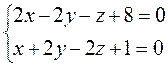
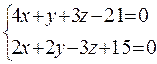
6. Составить уравнение плоскости, проходящей через точку (2,-3,1) и через прямую 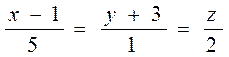
|
|
7. Установить, что 3 плоскости 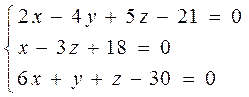 имеют общую точку и вычислить ее координаты с помощью матричного исчисления, методом Гаусса и по формуле Крамера.
имеют общую точку и вычислить ее координаты с помощью матричного исчисления, методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное поверхностями:
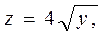
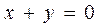
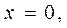
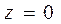
Вариант 2
1. Упростить уравнение и построить кривую:
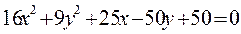
2. Даны 3 вектора: 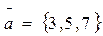
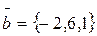
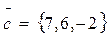
Найти: 
3. Найти площадь параллелограмма, построенного на векторах 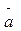 и
и 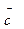 из задачи 2.
из задачи 2.
4. Даны стороны параллелограмма y = x – 2, 5y = x + 6. Диагонали его пересекаются в начале координат. Написать уравнения 2-х других сторон.
5. Составить уравнение прямой, проходящей через точку А(1,2,3) пересекающей ось OZ и перпендикулярной к прямой x = y = z
6. Написать уравнение плоскости, проходящей через прямые:
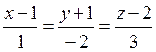
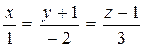
7. Найти точку пересечения плоскостей с помощью матричного исчисления. 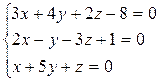 , а также методом Гаусса по формулам Крамера.
, а также методом Гаусса по формулам Крамера.
8. Построить тело, ограниченное поверхностями:
z = 4 – x2, x2 + y2 = 4, z = 0
Вариант 3
1. Упростить уравнение и построить кривую:
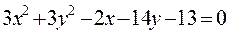
2. Даны 3 вектора: 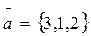
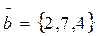
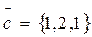
Найти: 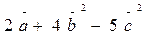
3. Обьем тетраэдра V=5, три его вершины А (2,1,-1), Б(3,0,1),
С(2,-1,3). Найти 4-ую вершину, если известно, что она лежит на оси ОУ.
4. Даны стороны параллелограмма y = x – 2, 5y = x + 6. Диагонали его пересекаются в начале координат. Написать уравнения его диагоналей.
5. Найти плоскость, проходящую через т. С(2,-1,1) перпендикулярно к линии пересечения 2 плоскостей:
3x – y – z + 1 = 0, x – y + 2z + 1 = 0
6. Провести уравнения прямой  к каноническому виду.
к каноническому виду.
7. Найти точку пересечения 3 плоскостей с помощью матричного исчисления: 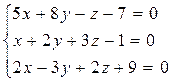 , а также методом Гаусса и по формулам Крамера.
, а также методом Гаусса и по формулам Крамера.
8. Построить тело ограниченное поверхностями:
z = (x – 1)2, y2 = x, z = 0
Вариант 4
1. Упростить уравнение и построить кривую.
x2 + y2 + 2x – 4y = 0
2. Найти численную величину проекции вектора 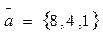 на ось, параллельную вектору
на ось, параллельную вектору 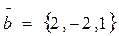 и угол между векторами
и угол между векторами 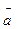 и
и 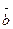
3. Найти площадь параллелограмма, построенного на векторах
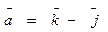 и
и 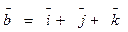
4. Составить уравнения сторон квадрата, зная одну из его вершин А(3,-4) и уравнения 2-х сторон 7x – 2y – 1=0, 2x + 7y – 6 =0
5. Написать уравнения прямой, проходящей через точку М(2,-3,4) и перпендикулярной к прямым:
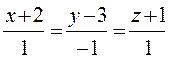
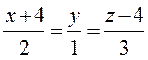
6. Через точку пересечения прямой 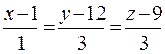 и плоскости
и плоскости
x + 3y – 5z – 2 = 0 провести плоскость параллельно к данной плоскости.
7. Найти точку пересечения 3 плоскостей с помощью матричного исчисления. 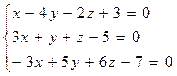 , а также методом Гаусса и по формуле Крамера.
, а также методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное поверхностями:
z = x2, 2x + 3y = 6, x = 0, z = 0
Вариант 5
1. Упростить уравнение и построить кривую:
16x2 + 4y2 – 5x + 7y = 0
2. Даны 2 вектора: 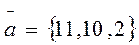 и
и 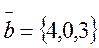 Найти вектор
Найти вектор 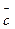 , перпендикулярный к векторам
, перпендикулярный к векторам 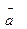 и
и 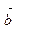 равный по длине единице и образующей с
равный по длине единице и образующей с 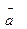 и
и 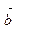 правую тройку.
правую тройку.
3. Найти V параллелепипеда, построенного на векторах 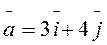
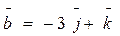
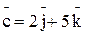
4. Составить уравнения сторон ∆АВС, если т. А(0,2) и уравнения высот ВМ: x + y = 4, CM: y = 2x, где т. М- пересечение высот.
5. Найти точку, симметричную т. А(2,1,0) относительно плоскости x – 2z + 1 = 0
6. Показать, что прямая 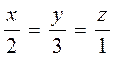 перпендикулярна к прямой
перпендикулярна к прямой 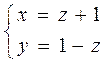
7. Найти точку пересечения 3 плоскостей с помощью матричного исчисления: 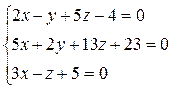 , а также по формулам Крамера и методам Гаусса.
, а также по формулам Крамера и методам Гаусса.
8. Построить тело, ограниченное поверхностями:
4z = y2, 2x – y = 0, x + y =9, z = 0
Вариант 6
1. Упростить уравнение и построить кривую:
7x2 – 14x + 24y + 5 = 0
2. Найти вектор 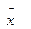 , удовлетворяющий одновременно трем уравнениям:
, удовлетворяющий одновременно трем уравнениям: 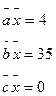 , где
, где 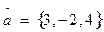
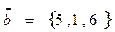
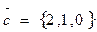
3. Найти Ѕ параллелограмма, построенного на векторах


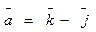
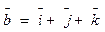
4. Найти точку, симметричную т. М(0,-3) относительно прямой
y + x + ½ = 0
5. Найти расстояние точки М(2,-1,3) до прямой 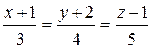
6. Написать уравнение плоскости, проходящей через прямые:
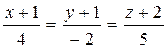
 и
и 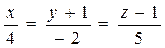
7. Найти точку пересечения 3 плоскостей с помощью матричного исчисления: 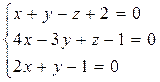 , а также по методам Гаусса и по формулам Крамера.
, а также по методам Гаусса и по формулам Крамера.
8. Построить тело, ограниченное поверхностями:
y2 = 4x, x2 = 4y, x + z = 2, z = 0
Вариант 7
1. Упростить уравнение и построить кривую:
3x2 + 3y2 – 12x – 12y + 4 = 0
2. Даны вершины треугольника: А(1,-1,2), В(1,3,-1), С(1,3,-1). Найти косинус угла АДС между медианой АД и стороной ВС и вычислить площадь АДС (с помощью векторной алгебры).
3. Вычислить пр 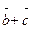 (
(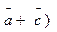 если
если 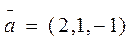 ;
; 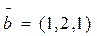 ;
; 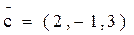
4. Дана прямая 2x + y – 6= 0 и на ней две т. А и В с ординатами yA=6, yB=-2. Найти длину высоты АД ∆АОВ, где О- начало координат.
5. Найти координаты углов между прямыми: 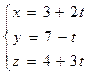
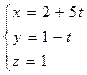
6. Написать уравнение плоскости, проходящей через точки (0,-5,0), (0,0,2) и перпендикулярной к плоскости x + 5y +2z – 10 = 0
7. Исследовать и решить с помощью матричного исчисления систему уравнений: 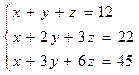 , а также методом Гаусса и по формуле Крамера.
, а также методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное поверхностями:
x2 + z2 – y2=0, y = + - 5
Вариант 8
1. Упростить уравнение и построить кривую:
x2 + y2 – 4x – 4y + 3 = 0
2. Даны 3 вектора: 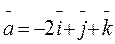 ,
, 
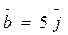 ,
, 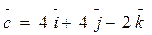
Вычислить V параллелепипеда, построенного на этих векторах.
3. Найти пр 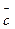 (
(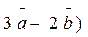 (
(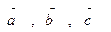 из задания 2)
из задания 2)
4. Даны уравнения 2-х высот ∆ x + y = 4, y = 2x и одна из его вершин А(0,2). Составить уравнение сторон ∆.
5. Найти проекцию точки (1,2,3) на плоскость 5x – y + 3z – 4 = 0
6. Найти расстояние от т. М0(2,-10,8) до плоскости, проходящей через точки М1(2,-4,-3); М2(5,-6,0); М3(-1,3,-3).
7. Исследовать и решить систему уравнений с помощью матричного исчисления: 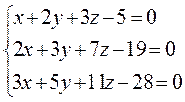 , а также методом Гаусса и по формуле Крамера.
, а также методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное поверхностями:
x+ y = 9, 2x = y, z = x2, z = 0
Вариант 9
1. Упростить уравнение и построить кривую:
5x2 + 12xy – 22x – 12y – 19 = 0
2. Вычислить площадь треугольника с помощью векторной алгебры, если вершины треугольника А(7,3,4.); В(1,0,6); С(4,5,-2).
3. Доказать, что векторы 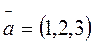 ;
; 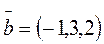 ;
; 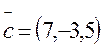 образуют базис.
образуют базис.
4. Точки А(5,1); В(2,-3); С(-1,7) являются вершинами треугольника. Составить уравнение медианы СД.
5. Доказать, что прямые 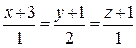 и
и 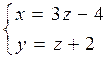 пересекаются, найти точку их пересечения.
пересекаются, найти точку их пересечения.
6. Написать уравнение плоскости, проходящей через точку (-1,-1,2) и перпендикулярной к плоскости x – 2y + z – 4 = 0; x + 2y– 2z + 4=0
7. Найти точку пересечения 3 плоскостей с помощью матричного исчисления: 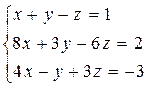 , а также методом Гаусса и по формуле Крамера.
, а также методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное поверхностями:
z = x2 + 3y2, x + y= 1, x = 0, y = 0, z = 0
Вариант 10
1. Упростить уравнение и построить кривую:
225x2 + 25y2 + 64x – 64y – 227 = 0
2. Даны векторы 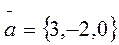 ;
; 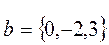 . Вычислить площадь треугольника, построенного на векторе
. Вычислить площадь треугольника, построенного на векторе 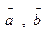
3. Найти пр 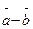
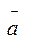 ,где
,где 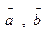 смотри в задании 2.
смотри в задании 2.
4. Написать уравнение прямой, проходящей через точку пересечения прямых x + 8y – 26 = 0, 4x + 7y + 29 = 0 параллельно вектору 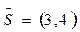
5. Написать уравнение плоскости, проходящей через точки (0,-5,0) и (0,0,2) и перпендикулярно плоскости x + 5y + 2z – 10 = 0.
6. Найти угол между прямыми:
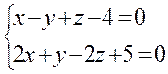
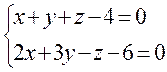
7. Найти точку пересечения 3 плоскостей с помощью матричного исчисления: 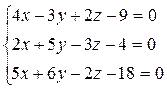 , а также методом Гаусса и по формуле Крамера.
, а также методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное поверхностями:
z2=1 – y, y = x2, z ≥ 0
Вариант 11.
1. Упростить уравнение и построить кривую:
3y2 + 16x + 12y – 36 = 0
2. Найти площадь параллелограмма, построенного на векторах:
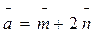 ,
, 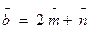 , где
, где 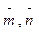 -единственные векторы, образующие угол π/6
-единственные векторы, образующие угол π/6
3. Найти площадь ∆АВС, где А(4,2,5); В(0,7,2); С(0,2,7).
4. Составить уравнение линии, все точки которой равноудалены от 2-х точек А(-2,1); В(1,-3)
5. Написать уравнение перпендикуляра, опущенного из точки
(1,0,-1) на прямую 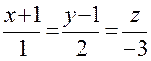
6. Найти площадь, проходящую через точку (2,2,2) и параллельную плоскости x – 2y – 3z = 0.
7. Исследовать и решить систему 3 уравнений с тремя неизвестными: 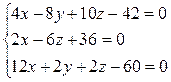 с помощью матричного исчисления, методом Гаусса и по формуле Крамера.
с помощью матричного исчисления, методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное поверхностями:
x2 = 2 – y, y = z2, x ≥ 2
Вариант 12
1. Упростить уравнение и построить кривую:
9x2 – 24xy + 16y2 – 20x + 110y – 50 = 0
2. Вычислить объем пирамиды с вершинами: О(0,0,0,); В(2,5,0); А(5,2,0); С(1,2,4).
3. Найти площадь грани АВС.
4. Определить траекторию т. М(x,y), которая при своем движении все время остается вдвое ближе к т. А(1,0), чем к т. В(4,0)
5. Показать, что прямая 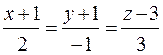 параллельна плоскости
параллельна плоскости
2x + y – z = 0, а прямая 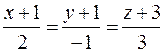 лежит в плоскости.
лежит в плоскости.
6. Найти расстояние между плоскостями: 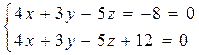
7. Найти точку пересечения 3 плоскостей с помощью матричного исчисления: 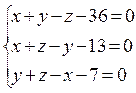 , а также методом Гаусса и по формуле Крамера.
, а также методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное поверхностями:
x= z2 + 5y2, z+ x = 2, x = 0, y = 0, z = 0
Вариант 13
1. Упростить уравнение и построить кривую:
14x2 + 21y2 – 4x + 18y – 139 = 0
2. Показать, что 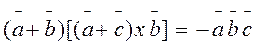
3. Разложить вектор 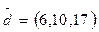 по базису
по базису 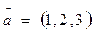 ,
, 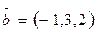 ,
,
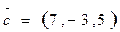
4. Даны 2 вершины А(-3,3) и В(5,-1) и точка D(4,3) пересечения высот треугольника. Составить уравнения его сторон.
5. Найти расстояние точки М(3,0,4) от прямой: 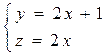
6. Найти угол между прямыми:
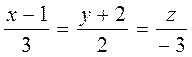 и
и 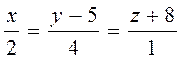
7. Найти точки пересечения 2 плоскостей с помощью матричного исчисления: 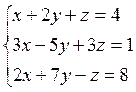 , а также методом Гаусса и по формуле Крамера.
, а также методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное поверхностями:
x2 + z2 = 4, x + y + z = 2, y = 1
Вариант 14.
1. Упростить уравнение и построить кривую:
6xy + 8y2 – 12x – 26y + 11 = 0
2. Показать, что: 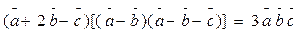
3. Вычислить диагональ и площадь параллелограмма, построенного на векторах 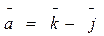 ,
, 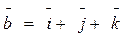
4. Уравнение 2 сторон параллелограмма x + 2y + 2 = 0 и x + y = 0, а уравнение одной из его диагоналей x – 2 = 0. Найти координаты вершин параллелограмма.
5. Написать уравнение прямой, проходящей через точку (2,-3,4) перпендикулярной оси OZ.
6. Найти точку пересечения прямой: 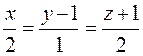 с помощью
с помощью
x + 2y + 3z – 29 = 0
7. Найти точку пересечения 3 плоскостей с помощью матричного исследования: 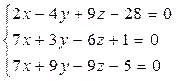 , а также методом Гаусса и по формуле Крамера.
, а также методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное поверхностями:
x + z = 5, 2x = z, y = x2, y = 1
Вариант 15.
1. Упростить уравнение и построить кривую:
x2 – 4xy + 4y2 + 4x – 3y – 7 = 0
2. Даны точки А(-2,3,-4); В(3,2,5); С(1,-1,2); Д(3,2,-4). Вычислить пр 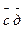
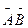 .
.
3. Вычислить объем параллелепипеда, построенного на векторах
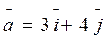 ;
; 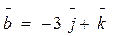 ;
; 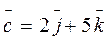
4. Даны уравнения одной из сторон ромба x – 3y + 10 = 0 и одной из его диагоналей x + 4y – 4 = 0; диагонали ромба пересекаются в точке (0,1). Найти уравнения остальных сторон ромба.
5. Найти проекцию точки А(1,2,8) на прямую: 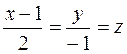
6. Найти уравнение плоскости, проходящей через линию пересечения плоскостей: 2x – y + 3z - 6 = 0; x + 2y –z + 3 = 0
и через точку А(1,2,4)
7. Найти точку пересечения 3 плоскостей с помощью матричного исчисления: 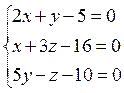 , а также методом Гаусса и по формуле Крамера.
, а также методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное плоскостями:
z2 = 4x, x2 = 4z, x + y = 2, y = 0
Вариант 16.
1. Упростить уравнение и построить кривую:
2x2 + 5xy + 2y2 – 6x – 3y – 8 = 0
2. Даны три вектора: 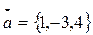 ;
; 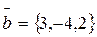 ;
; 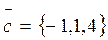
Вычислить пр 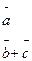
3. Вычислить 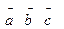 (см. векторы из задачи 2)
(см. векторы из задачи 2)
4. Даны векторы А(-3,-2); В(4,-1); С(1,3) трапеции АВСД (АД параллельно ВС). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершин Д этой точки.
5. Написать уравнения прямой, проходящей через точку А(0,-4,0) и параллельной вектору 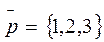
6. Составить уравнение плоскости, проходящей через прямую
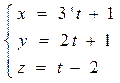 параллельной прямой
параллельной прямой 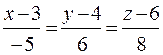
7. Найти точку пересечения трех плоскостей с помощью матричного исчисления: 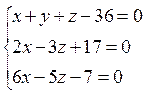 , а также методом Гаусса и по формуле Крамера.
, а также методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное поверхностями:
4x = y2, 2z – y = 0, z + y = 9, x = 0
Вариант 17.
1. Упростить уравнение и построить кривую:
9x2 + 24xy + 16y2 – 230x + 110y – 475 = 0
2. Даны две точки М(-5,7,-6), Н(7,-9,9). Вычислить проекцию вектора 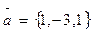 на ось вектора
на ось вектора 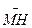
3. Найти координаты вектора 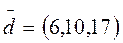 в базисе
в базисе 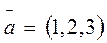 ;
;
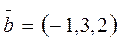 ;
; 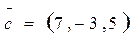
4. Даны уравнения двух сторон треугольника 5x – 4y + 15 = 0 и
4x + y – 9 =0. Его медианы пересекаются в точке (0,2). Составить уравнение третьей стороны треугольника.
5. Написать уравнение прямой, проходящей через т. А4(4,7,8) перпендикулярной плоскости, проходящей через т. А1(3,5,4); А2(8,7,4); А3(5,10,4)
6. Найти расстояние от т. А(4,3,0) до плоскости 3x + 4y – z + 6 =0
7. Найти точку пересечения 3 плоскостей с помощью матричного исчисления: 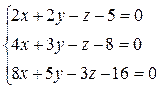 , а также методом Гаусса и по формуле Крамера.
, а также методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное поверхностями:
y = x2, z = 2, y + 3x = 8, z = 0, y = 0
Вариант 18.
1. Упростить уравнение и построить кривую:
2x2 + 4xy + 5y2 – 6x – 8y – 1 = 0
2. Даны векторы: 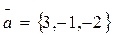 ;
; 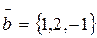 . Найти координаты векторного произведения
. Найти координаты векторного произведения 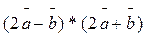
3. Показать, что векторы 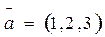 ;
; 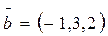 ;
; 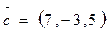 образует базис.
образует базис.
4. Даны две вершины А(2,-2) и В(3,-1) и точка Р(1,0) пересечения медиан ∆АВС. Составить уравнение высоты ∆, проведенной через третью вершину С.
5. Найти угол между прямыми:
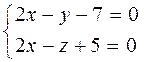
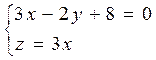
6. Написать уравнение плоскости, проходящей через т. М(-1,-1,2) и перпендикулярной к плоскости: 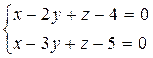
7. Найти точку пересечения трех плоскостей с помощью матричного исчисления: 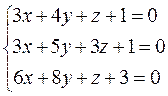 , а также методом Гаусса и по формуле Крамера.
, а также методом Гаусса и по формуле Крамера.
8. Построить тело, ограниченное поверхностями:
z = (y – 2)2, x2 = y, z = 1
Вариант 19.
1. Упростить уравнение и построить кривую:
5x2 + 5y2 – 16x – 16y – 16 = 0
2. Вычислить синус угла, образованного векторами: 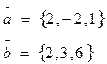
3. Установить, лежат ли точки А(2,-1,2); В(1,2,1); С(2,3,0);
Д(5,0,-6) в одной плоскости.
4. Даны уравнения двух высот ∆ x + y = 4 и y = 2x и одна из его вершин А(0,2). Составить уравнения сторон треугольника.
5. Найти расстояние от точки М(9,6,4) до прямой: 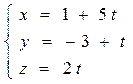
6. Составить уравнение плоскости, отстоящей от начала координат на расстояние 29 и перпендикулярной к прямой, по которой пересекаются плоскости: 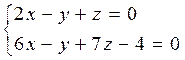
7. Исследовать и решить систему трех уравнений с тремя неизвестными с помощью матричного исчисления, методом Гаусса и по формулам Крамера: 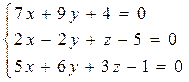
8. Построить тело, ограниченное поверхностями:
Y = 4 – x2, x2 + z2 = 4, y = 0
Вариант 20.
1. Упростить уравнение и построить прямую:
9x2 + 16y2 – 40x + 30y = 0
2. Даны векторы: 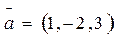 ;
; 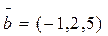 ;
; 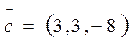 . Вычислить
. Вычислить 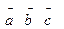
3. Найти площадь параллелограмма, построенного на векторах

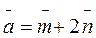 и
и 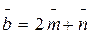 , где
, где 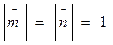 и угол между
и угол между 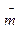 и
и 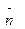 равен 300
равен 300
4. Даны уравнения двух медиан треугольника x – 2y + 1 = 0 и
y – 1 = 0 и одна из его вершин (1,3). Составить уравнения его сторон.
5. Составить уравнение прямой, проходящей через начало координат перпендикулярной прямой 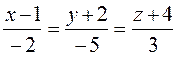
6. Составить уравнение плоскости, проходящей через прямую
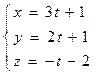 параллельно прямой
параллельно прямой 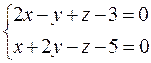
7. Исследовать и решить систему трех уравнений с помощью матричного исчисления: 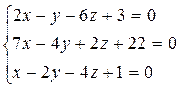 , а также методом Гаусса и по формулам Крамера.
, а также методом Гаусса и по формулам Крамера.
8. Построить тело, ограниченное поверхностями:
z = 0, z = 2x, x + y = 3, x = 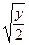
Вариант 21.
1. Упростить уравнение и построить прямую:
3x2 + 3y2 – 4x – 4y – 12 = 0
2. Даны вершины тетраэдра А(2,1,3); В(-2,1,4); С(6,3,8); Д(-8,4,5). Найти длину его высоты, опущенной из вершины Д.
3. Разложить вектор 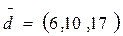 по базису
по базису 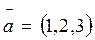 ;
; 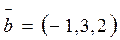 ;
; 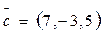
4. Две стороны треугольника заданы уравнениями 5x - 2y – 8 = 0,
3x - 2y – 8 = 0, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны.
5. Найти расстояние от точки (3,4,2) до прямой 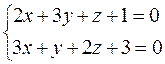
6. Составить уравнение биссекторных плоскостей углов между 2 плоскостями: 7x + y – 6 = 0; 3x + 5y – 4 + 1 = 0
7. Исследовать и решить систему трех уравнений с помощью матричного исчисления, а также методом Гаусса и по формуле Крамера: 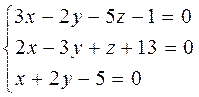
8. Построить тело, ограниченное поверхностями:
x2 + y2 = z2, x + y + z = 2, z = 0
Вариант 22
1. Упростить уравнение и построить кривую:
x2 + y2 – 4x – 4y + 12 = 0
2. Объем тетраэдра V=5, три его вершины находятся в точках А(2,1,-1); В(3,0,1); С(2,-1,3). Найти координаты четвертой вершины Д, если известно, что она лежит на оси OZ.
3. Найти пр 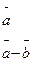 , если
, если 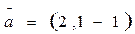 ;
; 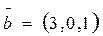 .
.
4. Уравнение одной из сторон квадрата x + 3y – 5 = 0. Составить уравнение трех остальных сторон квадрата (-1,0) – точка пересечения его диагоналей.
5. Найти точку А1 симметричную точке А(3,-1,4) относительно прямой: 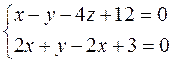
6. На оси OZ найти точку, равноудаленную от точки (2,3,4) и от плоскости 2x + 3y + z – 17 = 0.
7. Исследовать и решить систему уравнений с помощью матричного исчисления: 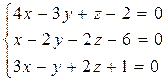 , а также методом Гаусса и по формулам Крамера.
, а также методом Гаусса и по формулам Крамера.
8. Построить тело, ограниченное поверхностями:
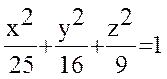 z ≥ 0, x + y + z = 4
z ≥ 0, x + y + z = 4
Вариант 23.
1. Упростить уравнение и построить кривую:
x2 + 2xy + y2 + 4x + 4y + 3 = 0
2. Установить, лежат ли векторы 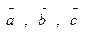 в одной плоскости если:
в одной плоскости если:
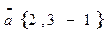 ;
; 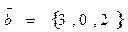 ;
; 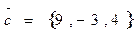
3. Найти пр 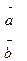 , если
, если 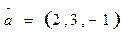
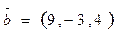
4. Составить уравнения сторон треугольника, зная одну из его вершин А(-4,2) и уравнения 2-х медиан: 3x-2y+2=0 и 3x+5y-12=0.
5. Написать уравнение прямой, проходящей через т. А(2,-1,0) параллельной прямой 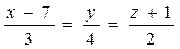
6. Найти расстояние точки (4,3,0) от плоскости, проходящей через М1(1,3,0); М2(4,-1,2) и М3(3,0,1)
7. Исследовать и решить систему уравнений с помощью матричного исчисления, а также по формулам Крамера и методом Гаусса: 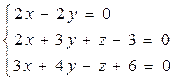
8. Построить тело, ограниченное поверхностями:
 x + y + z = 5
x + y + z = 5
Вариант 24.
1. Упростить уравнение и построить кривую:
x2 + 4y2 – 2x + 4y + 4 = 0
2. Доказать тождество:
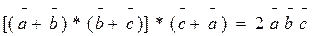
3. Найти площадь треугольника, вершин которого А(3,0,1);  В(4,5,6); С(-2,4,5)
В(4,5,6); С(-2,4,5)
4. Составить уравнения сторон треугольника, зная одну из его вершин А(-3,4) и уравнения 2-х вершин: x-2y-1=0; 2x-7y-6=0
5. Найти точки пересечения с плоскости координат прямой:
x= 6 + 2t, y = -2 – 4t, z = -5t
6. Написать уравнения плоскости, параллельной плоскости
3x-2y+2z+5=0 и удаленных от нее на 3 единицы.