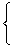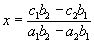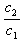В предыдущем разделе мы установили, что как только в линейном пространстве выбран базис, то каждому линейному преобразованию соответствует матрица этого преобразования. Однако если выбрать в пространстве другой базис, то матрица преобразования, как правило, станет другой. Выясним, как эти матрицы связаны между собой.
Пусть  --
-- 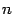 -мерное линейное пространство,
-мерное линейное пространство,  и
и 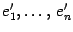 -- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть
-- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть 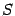 -- матрица перехода 19.1.4 а от старого базиса к новому.
-- матрица перехода 19.1.4 а от старого базиса к новому.
Предложение 19.1 Пусть 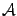 -- линейное преобразование пространства
-- линейное преобразование пространства 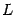 ,
, 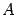 и
и  -- матрицы этого преобразования в старом и новом базисе соответственно. Тогда
-- матрицы этого преобразования в старом и новом базисе соответственно. Тогда

Доказательство. Пусть 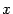 -- произвольный вектор пространства
-- произвольный вектор пространства 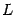 ,
,  -- его образ, то есть
-- его образ, то есть  . Пусть
. Пусть  и
и  -- координатные столбцы векторов
-- координатные столбцы векторов 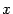 и
и  в старом базисе, а
в старом базисе, а 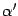 ,
, 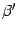 -- в новом. Тогда в силу формулы (19.3)
-- в новом. Тогда в силу формулы (19.3) 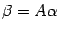 . По предложению 18.5 имеем
. По предложению 18.5 имеем  ,
, 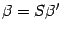 . Подставим эти выражения в предыдущую формулу, получаем
. Подставим эти выражения в предыдущую формулу, получаем 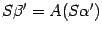 . Откуда
. Откуда 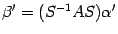 . С другой стороны, в силу формулы (19.3) в новом базисе
. С другой стороны, в силу формулы (19.3) в новом базисе  . Сравнивая это равенство с предыдущим, получаем
. Сравнивая это равенство с предыдущим, получаем 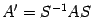 .
.
Определение 19.2 Две квадратных матрицы 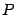 и
и 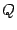 одного порядка называются подобными, если существует такая невырожденная матрица
одного порядка называются подобными, если существует такая невырожденная матрица 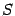 , что
, что  .
.
Следствие 19.1 Матрицы одного линейного преобразования, соответствующие разным базисам, подобны друг другу, и наоборот, если матрицы подобны, то они являются матрицами одного и того же преобразования в разных базисах.
Определение и примеры
Рассмотрим линейное пространство 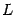 и преобразование
и преобразование 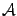 этого пространства, то есть закон, по которому каждому вектору
этого пространства, то есть закон, по которому каждому вектору 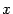 из
из 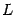 соответствует вектор
соответствует вектор 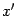 из того же пространства. Вектор
из того же пространства. Вектор 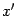 называется образом вектора
называется образом вектора 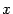 и обозначается
и обозначается  , а вектор
, а вектор 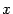 называется прообразом вектора
называется прообразом вектора 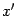 .
.
Определение 19.1 Преобразование 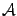 линейного пространства
линейного пространства 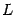 называется линейным, если для любых векторов
называется линейным, если для любых векторов 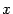 и
и  и любого числа
и любого числа  выполнены равенства
выполнены равенства
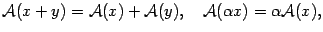
| (19.1) |
то есть образ суммы векторов равен сумме образов слагаемых, образ вектора, умноженного на число, равен произведению этого числа на образ вектора.
Замечание 19.1 В этой главе с каждым линейным преобразованием будет связана матрица, которую мы будем обозначать той же буквой, что и само преобразование. Чтобы их различать, мы для букв, обозначающих преобразование, будем использовать так называемый "каллиграфический" шрифт.
Линейное преобразование пространства 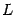 называют также линейным отображением из
называют также линейным отображением из 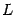 в
в 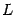 или линейным оператором из
или линейным оператором из 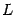 в
в  .
.
Исходя из равенств (19.1) легко проверить, что

то есть образ линейной комбинации векторов равен линейной комбинации их образов.
Рассмотрим несколько примеров линейных преобразований.
Пример 19.1 Пусть 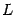 -- двумерное векторное пространство, то есть множество векторов плоскости. Пусть
-- двумерное векторное пространство, то есть множество векторов плоскости. Пусть 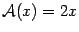 . Это преобразование действует так: каждый вектор оно переводит в вектор такого же направления, но в два раза большей длины. Если считать, что все векторы имеют начало в начале координат, то преобразование
. Это преобразование действует так: каждый вектор оно переводит в вектор такого же направления, но в два раза большей длины. Если считать, что все векторы имеют начало в начале координат, то преобразование 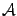 можно представить как растяжение плоскости в два раза (рис. 19.1).
можно представить как растяжение плоскости в два раза (рис. 19.1).
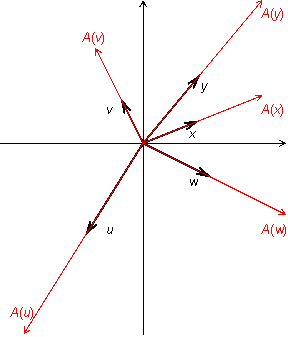
Рис.19.1.Преобразование растяжения
Проверим выполнение равенств (19.1)
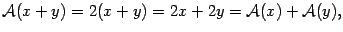
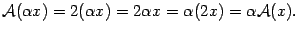
Равенства (19.1) выполнены, следовательно, преобразование  является линейным.
является линейным.
Пример 19.2 Пусть 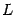 -- двумерное векторное пространство,
-- двумерное векторное пространство, 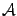 -- поворот вектора по часовой стрелке на угол
-- поворот вектора по часовой стрелке на угол 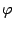 (рис. 19.2).
(рис. 19.2).

Рис.19.2.Преобразование поворота
Покажем, что это -- линейное преобразование.
Пусть 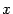 и
и  -- два вектора. Тогда
-- два вектора. Тогда 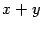 -- это диагональ параллелограмма со стронами
-- это диагональ параллелограмма со стронами 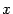 ,
,  (рис. 19.3).
(рис. 19.3).
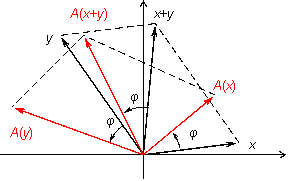
Рис.19.3.Образ суммы векторов
Если параллелограмм повернуть как единое целое на угол 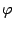 , то его стороны станут векторами
, то его стороны станут векторами  и
и  , диагональ будет вектором
, диагональ будет вектором 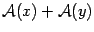 . С другой стороны, диагональ тоже повернулась на угол
. С другой стороны, диагональ тоже повернулась на угол 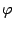 и поэтому является вектором
и поэтому является вектором 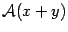 . Следовательно,
. Следовательно, 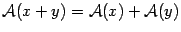 , первое из условий (19.1) выполнено.
, первое из условий (19.1) выполнено.
Пусть  -- число. Из рисунка 19.4 очевидно, что
-- число. Из рисунка 19.4 очевидно, что 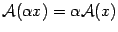 .
.

Рис.19.4.Образ вектора, умноженного на число
Следовательно, преобразование 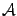 -- линейное.
-- линейное.
Упражнение19.1.1. Пусть 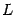 -- двумерное векторное пространство,
-- двумерное векторное пространство, 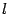 -- некоторая прямая, проходящая через начало координат,
-- некоторая прямая, проходящая через начало координат, 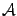 -- преобразование, переводящее каждый вектор
-- преобразование, переводящее каждый вектор 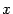 в вектор
в вектор 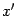 симметричный исходному относительно прямой
симметричный исходному относительно прямой 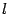 (рис. 19.5). Другими словами,
(рис. 19.5). Другими словами, 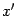 является зеркальным отражением вектора
является зеркальным отражением вектора 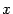 в прямой
в прямой 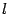 .
.

Рис.19.5.Преобразование отражения
Докажите, что 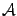 является линейным преобразованием.
является линейным преобразованием.
Упражнение19.1.2. Пусть 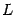 -- двумерное векторное пространство,
-- двумерное векторное пространство, 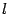 -- некоторая прямая, проходящая через начало координат,
-- некоторая прямая, проходящая через начало координат, 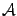 -- преобразование, переводящее каждый вектор
-- преобразование, переводящее каждый вектор 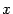 в его проекцию на прямую
в его проекцию на прямую 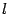 (рис. 19.6).
(рис. 19.6).
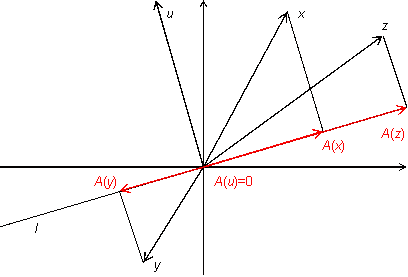
Рис.19.6.Преобразование проектирования
Докажите, что  является линейным преобразованием.
является линейным преобразованием.
Пример 19.3 Пусть  -- пространство всех многочленов,
-- пространство всех многочленов, 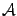 -- преобразование, которое переводит вектор из
-- преобразование, которое переводит вектор из 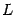 , то есть многочлен, в производную этого многочлена, которая естественно является многочленом, то есть вектором из
, то есть многочлен, в производную этого многочлена, которая естественно является многочленом, то есть вектором из 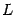 . Пусть
. Пусть 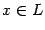 , то есть
, то есть  . Тогда
. Тогда
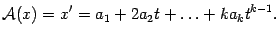
Например, если 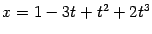 , то
, то 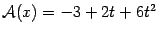 . Покажем, что преобразование
. Покажем, что преобразование 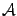 является линейным.
является линейным.
Пусть  ,
,  -- число. Тогда в силу свойства линейности производной получим
-- число. Тогда в силу свойства линейности производной получим

Аналогично,

Следовательно, 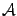 -- линейное преобразование.
-- линейное преобразование.
Пример 19.4 Пусть 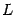 --
-- 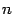 -мерное линейное пространство, Выберем в этом пространстве базис
-мерное линейное пространство, Выберем в этом пространстве базис 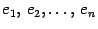 . Тогда у любого вектора
. Тогда у любого вектора 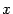 есть его координатный столбец
есть его координатный столбец 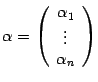 . Пусть
. Пусть 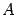 -- квадратная матрица порядка
-- квадратная матрица порядка 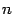 . Определим преобразование
. Определим преобразование 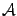 следующим образом:
следующим образом: 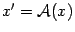 является вектором, координатный столбец которого равен
является вектором, координатный столбец которого равен  (справа стоит произведение матрицы
(справа стоит произведение матрицы 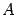 на столбец
на столбец  ). Покажем, что преобразование
). Покажем, что преобразование 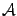 -- линейное.
-- линейное.
Пусть 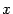 и
и  имеют координатные столбцы
имеют координатные столбцы  и
и  соответственно, а их образы
соответственно, а их образы  и
и  -- координатные столбцы
-- координатные столбцы 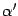 , и
, и 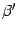 . Тогда
. Тогда
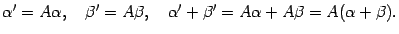
Но выражение в последнем равенстве справа является координатным столбцом образа суммы векторов 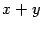 . Следовательно,
. Следовательно,  .
.
Пусть  -- произвольное число. Тогда координатный столбец вектора
-- произвольное число. Тогда координатный столбец вектора 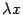 равен
равен 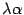 , координатный столбец образа вектора
, координатный столбец образа вектора
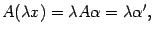
то есть равен числу  , умноженному на координатный столбец образа вектора
, умноженному на координатный столбец образа вектора 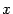 . Поэтому
. Поэтому  . Тем самым мы доказали, что преобразование
. Тем самым мы доказали, что преобразование 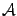 является линейным.
является линейным.
Очевидно, что примерами линейных преобразований могут служить тождественное преобразование, то есть преобразование, переводящее каждый вектор в себя, 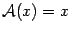 , и нулевое преобразование, переводящее каждый вектор в нуль,
, и нулевое преобразование, переводящее каждый вектор в нуль, 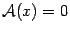 .
.
Легко проверяется, что для любого линейного преобразования 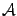 образ нуля равен нулю,
образ нуля равен нулю, 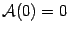 . Действительно, в силу второго из равенств (19.1)
. Действительно, в силу второго из равенств (19.1)
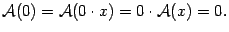
8) геометрический смысл определителя
| |||||||||||||||||||||||||||||||||||||||||||||||||
9)ортогональные матрицы
Ортогональная матрица
Ортогональная матрица — квадратная матрица A с вещественными элементами, результат умножения которой на AT равен единичной матрице:[1]
AAT = ATA = E,
или, что эквивалентно, её обратная матрица равна транспонированной матрице:
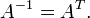
Свойства
· Столбцы и строки ортогональной матрицы образуют системы ортонормированных векторов, то есть:
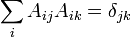
и

где 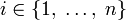 , n — порядок матрицы, а δ jk — символ Кронекера.
, n — порядок матрицы, а δ jk — символ Кронекера.
Другими словами, скалярное произведение строки на саму себя равно 1, а на любую другую строку — 0. Так же и для столбцов.
· Определитель ортогональной матрицы равен 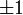 , что следует из свойств определителей:
, что следует из свойств определителей:

· Множество ортогональных матриц порядка n над полем k образует группу по умножению, так называемую ортогональную группу которая обозначается On (k) или 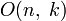 (если k опускается, то предполагается
(если k опускается, то предполагается 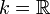 ).
).
· Ортогональные матрицы соответствуют линейным операторам, переводящим ортонормированный базис линейного пространства в ортонормированный.
· Любая вещественная ортогональная матрица подобна блочно-диагональной матрице с блоками вида
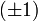 и
и 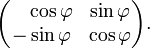
Примеры
· 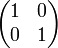 — единичная матрица
— единичная матрица
· 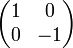
· 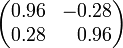 — пример матрицы поворота
— пример матрицы поворота
· 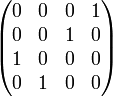 — пример перестановочной матрицы
— пример перестановочной матрицы
Подобная матрица
Квадратные матрицы A и B одинакового порядка называются подобными, если существует невырожденная матрица P того же порядка, такая что:

Подобные матрицы получаются при задании одного и того же линейного преобразования матрицей в разных координатных системах; при этом матрица Р является матрицей перехода от одной системы к другой.
Если две матрицы подобны, то говорят, что одна из матриц может быть получена преобразованием подобия из другой. Если при этом одна из матриц диагональная, то про вторую матрицу говорят, что она может быть диагонализована.
[править]Свойства
Отношение подобности матриц является отношением эквивалентности в пространстве квадратных матриц.
У подобных матриц совпадают многие характеристики, а именно:
§ ранг
§ определитель
§ след
§ собственные значения (но собственные векторы могут не совпадать)
§ характеристический многочлен
§ Жорданова форма с точностью до перестановки клеток
Можно доказать, что любая матрица A подобна AT.
[править]Канонические формы подобных матриц
Часто возникает вопрос, насколько сильно можно упростить вид заданного линейного преобразования путем замены базиса (т.е. системы координат). Поскольку получающиеся при этом матрицы подобны, то это то же самое, что и поиск некоторой канонической формы матрицы в классе эквивалентности матриц, подобных матрице этого линейного преобразования.
Простейшей такой формой была бы, конечно, диагональная матрица, но не все матрицы могут быть приведены к диагональному виду (важное исключение составляют симметричные действительные и эрмитовы матрицы, которые всегда могут быть диагонализованы).
Существует несколько более сложных канонических форм матриц, к которым может быть приведена любая матрица преобразованием подобия:
§ Жорданова нормальная форма
§ Фробениусова нормальная форма
10) диагонализация матрицы
Диагонализация матрицы
Используя тот факт, что матрица X L обратна к X R, из предыдущих формул получаем: X R-1 AX R = diag(l1,...,lN).Это является частным случаем преобразования подобия матрицы A: A -> Z -1 AZ для некоторой трансформирующей матрицы Z. Основную роль в вычислениях собственных значений играют именно преобразования подобия, поскольку они их не меняют. Это легко доказывается: det| Z -1 AZ - l 1 | = det| Z -1(A - l 1) Z | = det| Z | det| A - l 1 | det| Z |-1 = det| A - l 1 |.Видно, что матрица с набором собственных векторов, удовлетворяющим свойству полноты (к таким относятся все нормальные матрицы и "большинство" случаев ненормальных матриц), может быть диагонализирована преобразованием подобия, трансформирующей матрицей которого является матрица, столбцы которой содержат координаты правых собственных векторов; строки же обратной к ней матрицы будут образовывать координаты левых собственных векторов.
Для действительных симметричных матриц собственные векторы действительны и ортонормальны, таким образом, трансформирующая матрица является ортогональной. При этом преобразование подобия является ортогональным преобразованием:
A -> Z T AZ. Хотя действительные несимметричные матрицы и могут быть диагонализированы "почти во всех" случаях, трансформирующая матрица не обязательно будет действительной. Однако выходит так, что "почти" всю работу в этом случае делает также действительное преобразование подобия. Оно может привести матрицу к системе малых блоков (2 x 2), расположенных по диагонали; все остальные элементы будут нулевыми. Каждый из блоков размера (2 x 2) соответствует комплексно - сопряженной паре собственных чисел. Эта идея будет эксплуатироваться в алгоритмах, помещеных ниже.
Главная стратегия почти всех современных методов расчета собственных векторов и собственных значений заключается в том, что матрица A приводится к диагональной формы посредством цепочки преобразований подобия:
A -> P 1-1 AP 1 -> P 2-1 P 1-1 AP 1 P 2 -> P 3-1 P 2-1 P 1-1 AP 1 P 2 P 3 и т.д.
Если эта цепочка приводит в конце концов к диагональной форме, то матрица правых собственных векторов X R будет представлять из себя произведение матриц: X R = P 1 P 2 P 3...Иногда не требуется проводить подобное преобразование до диагональной формы. Например, если нас интересуют только собственные значения, а не собственные вектора, то достаточно привести A к треугольному виду, при котором нулями являются все элементы над диагональю или под ней. В этом случае диагональные элементы преобразованной матрицы уже будут собственными значениями.
Имеется два существенно различных подхода к осуществлению указанной стратегии. Часто они хорошо работают в комбинации друг с другом, так что большинство современных методов используют оба из их. Первый подход заключается в построении индивидуальных матриц P i как явных "элементарных" трансформаторов, расчитанных на специфические задачи, например, для обнуления конкретного внедиагонального элемента (преобразование Якоби) или целого столбца или строки (преобразования Хаусхолдера). В общем случае конечная цепочка подобных преобразований диагонализировать матрицу не может. Имеется выбор: либо использовать конечное число трансформаций для прохода большей части пути к диагонализации (например, приведя к трехдиагональной или Гессенберговской форме), а затем завершить операцию на второй стадии с помощью алгоритмов, которые будут указаны ниже. Либо итерациями свести внедиагональные элементы к пренебрежимо малым. Последний подход концептуально является простейшим и будет обсуждаться в следующем разделе, однако при N больших ~10 он является примерно в 5 раз менее эффективен.
Другой подход, называемый методами факторизации, более тонкий. Предположим, матрица A может быть разложена в произведение правого F R и левого F L факторов. Тогда
A = F L F R, или, что эквивалентно, F L-1 A = F R.Если мы перемножим эти факторы в обратном порядке и используем вышенаписанное тождество, то будем иметь F R F L = F L-1 AF L,что сразу распознается как преобразование подобия матрицы A с трансформирующей матрицей F L. Эту идею использует метод QR-разложения матрицы.
Методы факторизации также не дают сходимость за конечное число шагов. Но лучшие из них сходятся быстро и надежно, и при использовании хорошего начального состояния матрицы, первично преобразованной элементарными операциями, являются главным выбором.
Нормальную (в частности симметричную) матрицу A можно привести к диагональному виду преобразованием подобия —
A = TΛT −1
Здесь Λ = diag(λ1,..., λ N) — это диагональная матрица, элементами которой являются собственные значения матрицы A, а T — это матрица, составленная из соответствующих собственных векторов матрицы A, т.е. T = (v 1,..., v N).
Например,

Рис. 23 Приведение к диагональному виду
12) различные формы уравнения прямой на плоскости
Уравнение прямой, проходящей через точку c координатами (х0;у0) с известным угловым коэффициентом:
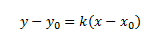
Уравнение прямой проходящей через две точки:

Уравнение прямой в отрезках на координатных осях:
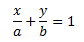
Расстояние от точки c координатами (х0;у0) до прямой Ах+Ву+С=0:
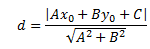
19) свойства сходящихся последовательностей
Иногда удобно записывать определение сходимости последовательности { an }  a в следующих эквивалентных первоначальному видах
a в следующих эквивалентных первоначальному видах
1. an  a, если
a, если 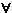

 0
0 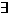 N (
N ( )
) 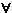 n
n  N (
N ( ): a -
): a - 
 an
an  a +
a + 
2. an  a, если
a, если 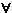

 0
0 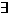 N (
N ( )
) 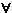 n
n  N (
N ( ): an
): an 
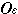 (a)
(a)
3. { an } 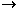 a, если
a, если 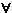

 0 вне окрестности
0 вне окрестности 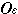 (a) лежит конечное число элементов
(a) лежит конечное число элементов
последовательности { an }.
Свойство 3.2.1 Если последовательность { an } сходится, то ее предел единственный.
Доказательство: (от противного) Пусть

Возьмем 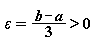
тогда 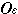 (a)
(a) 
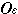 (b) =
(b) = 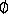 по выбору
по выбору  , с другой стороны, по определению сходимости,
, с другой стороны, по определению сходимости,
по 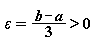
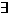 N 1
N 1 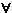 n
n  N 1: xn
N 1: xn 
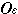 (a)
(a)
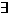 N 2
N 2 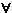 n
n  N 2: xn
N 2: xn 
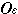 (b)
(b)
Следовательно, для n  max { N 1, N 2 }: xn
max { N 1, N 2 }: xn 
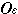 (a)
(a) 
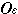 (b), что означает непустоту этого пересечения. Получено противоречие.
(b), что означает непустоту этого пересечения. Получено противоречие.
Последовательность { an } называется ограниченной, если 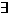 М
М  0
0 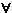 n: | an |
n: | an |  М. Это означает, что
М. Это означает, что
{ an }  [ - M, M ] или, что множество { an } можно накрыть отрезком [ - M, M ].
[ - M, M ] или, что множество { an } можно накрыть отрезком [ - M, M ].
Замечание 3.2.1 Ясно, что последовательность { an } будет ограниченной, если ее можно накрыть отрезком
[ - M, M ], начиная с некоторого номера N. (Вне отрезка [ - M, M ] может лежать лишь конечное число элементов последовательности { an }, следовательно, и всю последовательность можно накрыть некоторым отрезком [ - M, M 1 ], где М  M 1).
M 1).
Свойство 3.2.2 Если последовательность сходится, то она ограничена
Доказательство: Пусть an  a и
a и  = 1. Тогда, по определению сходимости, существует N, что для всех
= 1. Тогда, по определению сходимости, существует N, что для всех
n  N: | an - a |
N: | an - a |  1. Следовательно, | an | - | a |
1. Следовательно, | an | - | a |  | an - a |
| an - a |  1, и, поэтому,
1, и, поэтому, 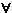 n
n  N: | an |
N: | an |  | a | + 1 = M,
| a | + 1 = M,
итак, по замечанию 3.2.1, последовательность { an } ограничена.
Свойство 3.2.3 Если последовательность { an } сходится к числу a  0, то вся последовательность { an } лежит вне окрестности нуля
0, то вся последовательность { an } лежит вне окрестности нуля 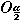 (0), начиная с некоторого номера.
(0), начиная с некоторого номера.
Для доказательства достаточно взять  0 .
0 .
Тогда, по определению предела, найдется N ( ), что для всех n
), что для всех n  N (
N (