Предел произведения нескольких функций равен произведению пределов этих функций:
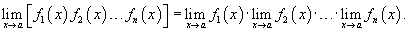
5) Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

23) верхний и нижний предел в точке
Частичным пределом последовательности называется предел какой-либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел. В противном случае, говорят, что у последовательности нет частичных пределов. В некоторой литературе в случаях, если из последовательности удаётся выделить бесконечно большую подпоследовательность, все элементы которой одновременно положительны или отрицательны, её частичным пределом называют соответственно  или
или  .
.
Нижний предел последовательности — это наименьший элемент множества частичных пределов последовательности.
Верхний предел последовательности — это наибольший элемент множества частичных пределов последовательности.
Иногда нижним пределом последовательности называют наименьшую из её предельных точек, а верхним — наибольшую.[1]Очевидно, что эти определения эквивалентны.
[править]Обозначения
Нижний предел последовательности  :
:
§  (в отечественной литературе);
(в отечественной литературе);
§  (в иностранной литературе).
(в иностранной литературе).
Верхний предел последовательности  :
:
§ 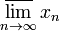 (в отечественной литературе);
(в отечественной литературе);
§  (в иностранной литературе).
(в иностранной литературе).
[править]Примеры
§ 
§ 
§ 
§  (в другой терминологии оба предела равны
(в другой терминологии оба предела равны  )
)
[править]Свойства
§ Частичным пределом последовательности может быть только её предельная точка, и, наоборот, любая предельная точка последовательности представляет собой некоторый её частичный предел. Иными словами, понятия «частичный предел последовательности» и «предельная точка последовательности» эквивалентны.
§ У любой ограниченной последовательности существуют и верхний, и нижний пределы (в множестве вещественных чисел). Если же считать  и
и  допустимыми значениями частичного предела, то верхний и нижний пределы существуют вообще у любой числовой последовательности.
допустимыми значениями частичного предела, то верхний и нижний пределы существуют вообще у любой числовой последовательности.
§ Числовая последовательность 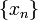 сходится к
сходится к  тогда и только тогда, когда
тогда и только тогда, когда 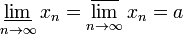 .
.
§ Для любого наперёд взятого положительного числа  все элементы ограниченной числовой последовательности
все элементы ограниченной числовой последовательности  , начиная с некоторого номера, зависящего от
, начиная с некоторого номера, зависящего от  , лежат внутри интервала
, лежат внутри интервала 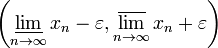 .
.
§ Если за пределами интервала  лежит лишь конечное число элементов ограниченной числовой последовательности
лежит лишь конечное число элементов ограниченной числовой последовательности  , то интервал
, то интервал  содержится в интервале
содержится в интервале  .
.
29)
| Теорема (Дарбу): |
Пусть  дифференцируема на дифференцируема на  . Тогда . Тогда 
|
| Доказательство: |

|
Для определенности считаем, что  , обратный случай доказывается аналогично.
Рассмотрим вспомогательную функцию , обратный случай доказывается аналогично.
Рассмотрим вспомогательную функцию 
 .
По определению производной, .
По определению производной,  При
При  Аналогично рассмотрим
Аналогично рассмотрим 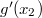 : при : при  Функция
Функция 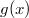 — дифференцируема, а значит, также и непрерывна на — дифференцируема, а значит, также и непрерывна на  , поэтому на этом отрезке существуют минимальное и максимальное значения функции. Из двух предыдущих неравенств следует, что минимальное значение достигается не в граничной точке.
Пусть оно достигается в точке , поэтому на этом отрезке существуют минимальное и максимальное значения функции. Из двух предыдущих неравенств следует, что минимальное значение достигается не в граничной точке.
Пусть оно достигается в точке  , тогда по теореме Ферма в этой точке , тогда по теореме Ферма в этой точке 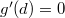 . Значит, . Значит, 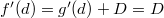 . .
|

|
| Теорема (Ферма): |
Пусть  существует и дифференцируема в существует и дифференцируема в  , и , и  — точка локального экстремума. Тогда — точка локального экстремума. Тогда 
|
| Доказательство: |

|
Рассмотрим случай, когда  — точка локального минимума. Случай с локальным максимумом доказывается аналогично. — точка локального минимума. Случай с локальным максимумом доказывается аналогично.
 ; рассмотрим ; рассмотрим  .
Заметим, что, по определению локального минимума, .
Заметим, что, по определению локального минимума,  .
Возможны 2 случая для .
Возможны 2 случая для  :
1. :
1.  2.
2.  Отсюда,
Отсюда,  . .
|

|
Замечание: обратная теорема не всегда верна, например,  но
но  — не экстремум.
— не экстремум.
| Определение: |
Корень уравнения  называется стационарной точкой. называется стационарной точкой.
|