Вариант № 32374511
Задание 1 № 516262
Установка счётчиков холодной и горячей воды стоит 2100 рублей. До установки счётчиков за водоснабжение платили 1100 рублей ежемесячно. После установки счётчиков ежемесячная оплата стала 700 рублей. Через сколько месяцев экономия впервые превысит затраты на установку счётчиков, если тарифы на воду не изменятся?
Решение.
Установка счетчиков позволяет ежемесячно экономить 1100 − 700 = 400 руб. Значит, они окупятся через 2100: 400 = 5,25 месяца или за 6 полных месяцев.
Ответ: 6
Задание 2 № 514175
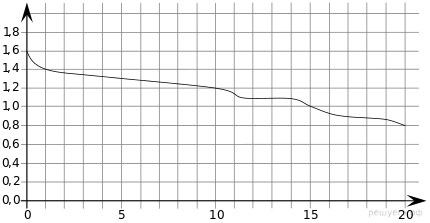
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, за сколько часов напряжение упадёт с 1,4 вольта до 1 вольта.
Решение.
Из графика видно, что напряжение падает с 1,4 вольта до 1 вольта за 15 − 1 = 14 часов.
Ответ: 14.
Задание 3 № 5191
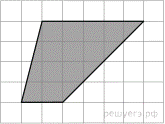Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см 
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту. Поэтому
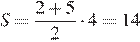см2.
Ответ: 14.
Задание 4 № 508961
В торговом центре два одинаковых автомата продают кофе. Обслуживание автоматов происходит по вечерам после закрытия центра. Известно, что вероятность события «К вечеру в первом автомате закончится кофе» равна 0,25. Такая же вероятность события «К вечеру во втором автомате закончится кофе». Вероятность того, что кофе к вечеру закончится в обоих автоматах, равна 0,15. Найдите вероятность того, что к вечеру дня кофе останется в обоих автоматах.
|
|
Решение.
Рассмотрим события
А = кофе закончится в первом автомате,
В = кофе закончится во втором автомате.
Тогда
A·B = кофе закончится в обоих автоматах,
A + B = кофе закончится хотя бы в одном автомате.
По условию P(A) = P(B) = 0,25; P(A·B) = 0,15.
События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
P(A + B) = P(A) + P(B) − P(A·B) = 0,25 + 0,25 − 0,15 = 0,35.
Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,35 = 0,65.
Ответ: 0,65.
Приведем другое решение.
Вероятность того, что кофе останется в первом автомате равна 1 − 0,25 = 0,75. Вероятность того, что кофе останется во втором автомате равна 1 − 0,25 = 0,75. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,15 = 0,85. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,85 = 0,75 + 0,75 − х, откуда искомая вероятость х = 0,65.
Примечание.
Заметим, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: P(A·B) = 0,25·0,25 = 0,0625, однако, по условию, эта вероятность равна 0,15.
Задание 5 № 513419
Найдите корень уравнения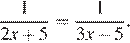 
Решение.
##
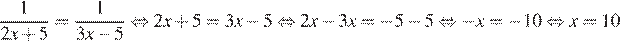
Ответ: 10
Задание 6 № 27793
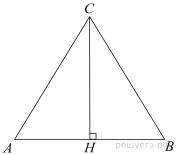В равностороннем треугольнике 
высот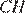а 
равна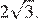 
Найдите стороны этого треугольника.
Решение.
треугольник 
– равносторонний, значит, все углы в треугольнике равны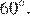 
|
|
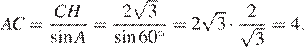
Ответ: 4.
Задание 7 № 120715
Прямая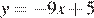 
является касательной к графику функции 
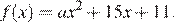Найдите a.
Решение.
Прямая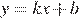 
является касательной к графику функции 
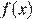в точке 
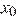тогда и только тогда, когда одновременно 
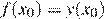и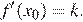 
В нашем случае имеем:
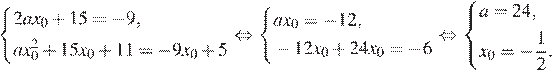
Искомое значение а равно 24.
Ответ: 24.
Приведем другое решение.
По смыслу задачи a ≠ 0, а значит, график заданной функции — парабола. Касательная к параболе (а также и к гиперболе) имеет с ней единственную общую точку. Поэтому необходимо и достаточно, чтобы уравнение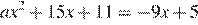 
имело единственно решение. Для этого дискриминант 
уравнения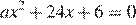 
должен быть равен нулю, откуда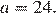 
Задание 8 № 73815
Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в шестнадцать раз?
Решение.
Объёмы подобных тел относятся как куб коэффициента подобия. Поэтому если все ребра увеличить в 16 раз, объём увеличится в 4096 раз.
Ответ: 4096.
Задание 9 № 502305
Найдите значение выражения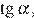 
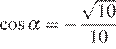если 
и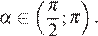 
Решение.
Поскольку угол альфа лежит во второй четверти, его тангенс отрицателен. Поэтому
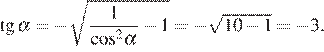
Ответ: −3.
Задание 10 № 42843
Уравнение процесса, в котором участвовал газ, записывается в виде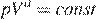 
, где p (Па) — давление в газе, V — объeм газа в кубических метрах, a — положительная константа. При каком наименьшем значении константы a уменьшение в 9 раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 27 раз?
Решение.
Пусть 
и 
– начальные, а 
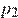и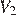 
– конечные значения объема и давления газа, соответственно. Условие 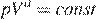означает, что 
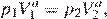откуда 
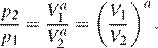Задача сводится к решению неравенства 
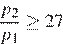, причем по условию 
:
|
|
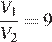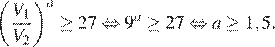
Ответ: 1,5.
Задание 11 № 523398
Первый и второй насосы, работая вместе, наполняют бассейн за 80 минут, второй и третий, работая вместе, — за 90 минут, а первый и третий, работая вместе, — за 240 минут. За сколько минут заполнят бассейн все три насоса, работая вместе?
Решение.
Наименьшее общее кратное чисел 80, 90 и 240 равно 720. За 720 минут первый и второй, второй и третий, первый и третий насосы (каждый учтен дважды) заполнят 9 + 8 + 3 = 20 бассейнов. Следовательно, работая одновременно, первый, второй и третий насосы заполняют 10 бассейнов за 720 минут, а значит, 1 бассейн за 72 минуты.
Ответ: 72.