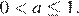За одну минуту первый и второй насосы заполнят 1/80 бассейна, второй и третий — 1/90 бассейна, а первый и третий — 1/240 бассейна. Работая вместе, за одну минуту два первых, два вторых и два третьих насоса заполнят
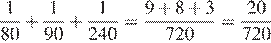бассейна.
Тем самым, они могли бы заполнить бассейн за 720/20 минуты или за 36 минут. Поскольку каждый из насосов был учтен два раза, в реальности первый, второй и третий насосы, работая вместе, могут заполнить бассейн за 72 минуты.
Задание 12 № 524071
Найдите точку минимума функции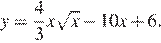 
Решение.
Найдем производную заданной функции:
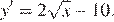
Найдем нули производной:
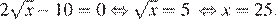
Определим знаки производной функции и изобразим на рисунке поведение функции:
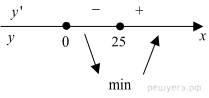
Искомая точка минимума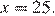 
Ответ: 25.
Задание 13 № 511453
Решите уравнение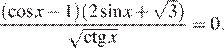 
Решение.
Левая часть уравнения имеет смысл при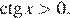 
Приравняем числитель к нулю:
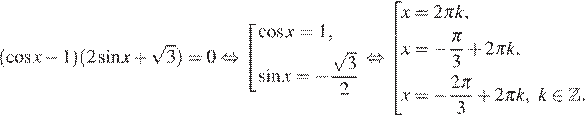
Учитывая условие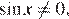 
получаем, что числа 
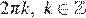не являются решениями данного уравнения. Учитывая условие 
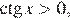получаем, что числа 
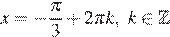не являются решениями данного уравнения. Тогда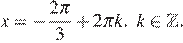 
Ответ: 
Задание 14 № 513259
Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Расстояние между этими хордами равно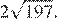 
а) Докажите, что центры оснований цилиндра лежат по одну сторону от этой плоскости.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
Решение.
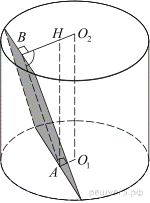
а) Заметим, что хорда длиной 12 находится на расстоянии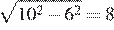 
от центра окружности основания, а хорда длиной 16, аналогично, — на расстоянии 6. Поэтому расстояние между их проекциями на плоскость, параллельную основаниям цилиндров, составляет либо 8 + 6 = 14, либо 8 − 6 = 2. Тогда расстояние между хордами составляет либо 
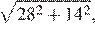либо 
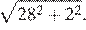По условию реализовался второй случай, в нем проекции хорд лежат по одну сторону от оси цилиндра. Значит, ось не пересекает данную плоскость в пределах цилиндра, то есть основания лежат по одну сторону от нее.
б) Обозначим центры оснований за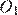 
и 
Проведем из центра основания с хордой длины 12 серединный перпендикуляр к этой хорде (он имеет длину 8, как уже отмечалось) и из центра другого основания — к другой хорде. Они лежат в одной плоскости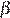 
, перпендикулярной этим хордам. Назовем середину меньшей хорды B, большей A и проекцию A на второе основание —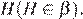 
Тогда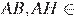 
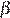и, значит, AB, AH перпендикулярны хорде, то есть прямой пересечения основания с данной плоскостью.
Значит, искомый угол равен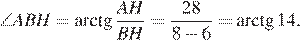 
Ответ: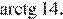 
Задание 15 № 515764
Решите неравенство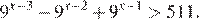 
Решение.
Решим неравенство:
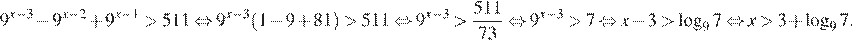
Ответ: 
Задание 16 № 518146
В треугольник ABC, в котором длина стороны AC больше длины стороны BC, вписана окружность с центром O. Точка B 1 симметрична точке B относительно прямой CO.
а) Докажите, что A, B, O и B 1 лежат на одной окружности.
б) Найдите площадь четырёхугольника ABOB 1, если AB = 10, AC = 8 и BC = 6.
Решение.
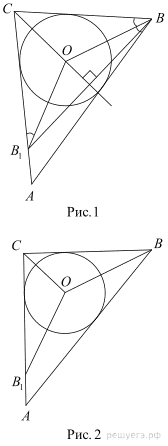
а) Луч CO является биссектрисой угла ACB, поэтому точка B 1 лежит на отрезке AC (рис. 1). Луч BO является биссектрисой угла ABC, поэтому
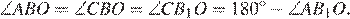
Значит, около четырёхугольника ABOB 1 можно описать окружность.
б) Треугольник ABC прямоугольный (рис. 2), поскольку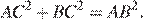 
Радиус r вписанной в него окружности равен
Найдем площади треугольников ABC, BOC и B 1 OC:
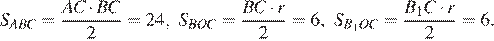
Треугольник ABC составлен из четырёхугольника ABOB 1 и треугольников BOC и B 1 OC. Значит, площадь четырёхугольника ABOB 1 равна
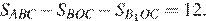
Ответ: б) 12.
Задание 17 № 514725
В июле 2016 года планируется взять кредит в банке на три года в размере S млн рублей, где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 |
| Долг (в млн рублей) | S | 0,7 S | 0,4 S |
Найдите наибольшее значение S, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.
Решение.
Долг перед банком (в млн рублей) на июль каждого года должен уменьшаться до нуля следующим образом:
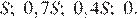
По условию, в январе каждого года долг увеличивается на 25%, значит, долг в январе каждого года равен:
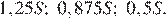
Следовательно, выплаты с февраля по июнь каждого года составляют:
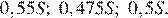
По условию, разность между наибольшей и наименьшей выплатами должна быть меньше 1 млн рублей:
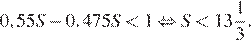
Наибольшее целое решение этого неравенства — число 13. Значит, искомый размер кредита — 13 млн рублей.
Ответ: 13.
Задание 18 № 514388
Найдите все значения a, при каждом из которых система уравнений
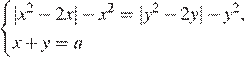
имеет более двух решений.
Решение.
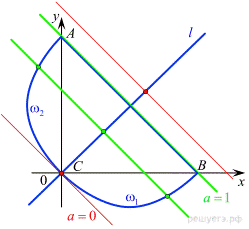
Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы.
Рассмотрим четыре случая:
1) Если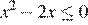 
и 
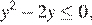то получаем уравнение
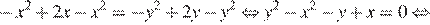
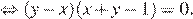
Полученное уравнение задаёт пару прямых 
и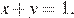 
Случаю удовлетворяют отрезки внутри квадрата 
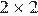с вершиной в начале координат.
2) Если 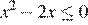и 
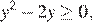то получаем уравнение
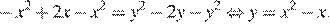
Полученное уравнение задаёт параболу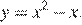 
Случаю удовлетворяет только дуга ниже оси Ox.
3) Если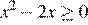 
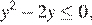и то получаем уравнение
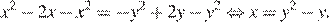
Полученное уравнение задаёт параболу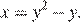 
Случаю удовлетворяет только дуга левее оси Oy.
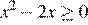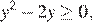4) Если и то получаем уравнение
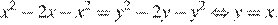
Полученное уравнение задаёт прямую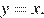 
Случаю удовлетворяют лучи вне квадрата 
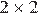с вершиной в начале координат.
Точки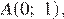 
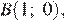
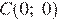являются точками пересечения полученных парабол с полученными прямыми и лежат на прямых 
и/или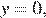 
поэтому искомое множество состоит из прямой l, задаваемой уравнением 
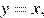отрезка AB прямой 
дуги 
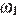параболы 
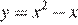с концами в точках B и C и дуги 
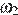параболы 
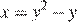с концами в точках A и C (см. рис.)
Рассмотрим второе уравнение системы. Оно задаёт прямую m, параллельную прямую AB или совпадающую с ней.
Заметим, что при a = 0 прямая m касается парабол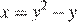 
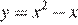и в точке C.
При a = 1 прямая m содержит отрезок AB, то есть исходная система имеет бесконечное число решений.
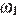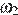При a = 0 прямая m касается дуг и в точке C, пересекает прямую l в точке C и не пересекает отрезок AB, то есть исходная система имеет одно решение.
При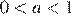 
прямая m не пересекает отрезок AB, пересекает прямую l в точке, отличной от точки C, и пересекает каждую из дуг 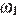и 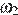в одной точке, отличной от точки C, то есть исходная система имеет три решения.
Пр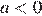и 
или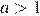 
прямая m пересекает прямую l в одной точке и не пересекает дуги 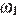и 
и отрезок AB, то есть исходная система имеет одно решение.
Значит, исходная система имеет более двух решений при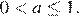 
Ответ: 