| Месяцы | Июль | Август | Сентябрь | Октябрь | Ноябрь | Декабрь |
| Средняя заработная плата за месяц |
Таблица 5.5
Динамика розничных цен на потребительские товары
по г. Находка с 1995-1999 г. (в процентах)
| Годы | |||||
| Динамика розничных цен (%) | 222,3 | 122,3 | 110,1 | 171,2 | 131,8 |
При составлении динамических рядов надо соблюдать следующее правило: уровни рядов должны быть сопоставимыми – это значит однородность показателей по экономическому содержанию, по территории, по кругу охватываемых объектов, по единице измерения. Эти измерения должны рассматриваться по единой методике.
Следовательно, прежде чем анализировать ряд динамики, необходимо исходить из цели исследования, обеспечить сопоставимость уровней ряда дополнительными расчетами, т.е. произвести смыкание рядов динамики.
11. Статические показатели ряда динамики.
При изучении динамики используются различные показатели и методы анализа, как элементарные, более простые, так и более сложные, требующие соответственно применения более сложных разделов математики.
Простейшими показателями анализа, которые используются при решении ряда задач, в первую очередь при измерении скорости изменения уровня ряда динамики, являются абсолютный прирост, темпы роста и прироста, а также абсолютное значение (содержание) одного процента прироста. Расчет этих показателей основан на сравнении между собой уровней ряда динамики. При этом уровень, с которым производится сравнение, называется базисным, так как он является базой сравнения. Обычно за базу сравнения принимается либо предыдущий, либо какой-либо предшествующий уровень, например первый уровень ряда.
Если каждый уровень сравнивается с предыдущим, то полученные при этом показатели называются цепными, так как они представляют собой как бы звенья «цепи», связывающей между собой уровни ряда. Если же все уровни связываются с одним и тем же уровнем, выступающим как постоянная база сравнения, то полученные при этом показатели называются базисными.
Часто построение ряда динамики начинают с того уровня, который будет использован в качестве постоянной базы сравнения. Выбор этой базы должен быть обоснован историческими и социально-экономическими особенностями развития изучаемого явления. В качестве базисного целесообразно брать какой-либо характерный, типичный уровень, например конечный уровень предыдущего этапа развития (или средний его уровень, если на предыдущем этапе уровень то повышался, то понижался).
Абсолютныш прирост показывает, на сколько единиц увеличился (или уменьшился) уровень по сравнению с базисным, т. е. за тот или иной промежуток (период) времени. Абсолютный прирост равен разности между сравниваемыми уровнями и измеряется в тех же единицах, что и эти уровни:
? =yi?yi?1;
? =yi?y0,
где уi – уровень i-го года; yi-1 – уровень предшествующего года; y0 – уровень базисного года. Если уровень уменьшился по сравнению с базисным, то? ‹ 0; он характеризует абсолютное уменьшение уровня.
Абсолютный прирост за единицу времени (месяц, год) измеряет абсолютную скорость роста (или снижения) уровня. Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных приростов равна соответствующему базисному приросту, т. е. общему приросту за весь период.
Более полную характеристику роста можно получить только тогда, когда абсолютные величины дополняются относительными. Относительными показателями динамики являются темпы роста и темпы прироста, характеризующие интенсивность процесса роста.
Темп роста (Тр) – статистический показатель, который отражает интенсивность изменения уровней ряда динамики и показывает, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения – какую часть базисного уровня составляет сравниваемый уровень; измеряется отношением текущего уровня к предыдущему или базисному:

Как и другие относительные величины, темп роста может быть выражен не только в форме коэффициента (простого отношения уровней), но и в процентах. Как и абсолютные приросты, темпы роста для любых рядов динамики сами по себе являются интервальными показателями, т. е. характеризуют тот или иной промежуток (интервал) времени.
Между цепными и базисными темпами роста, выраженными в форме коэффициентов, существует определенная взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста за весь соответствующий период, например: y2/ y1 y3/ y2 = y3/ y1.
Темп прироста (Тпр) характеризует относительную величину прироста, т. е. представляет собой отношение абсолютного прироста к предыдущему или базисному уровню:
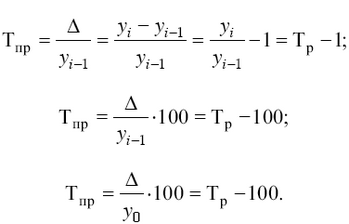
Темп прироста, выраженный в процентах, показывает, на сколько процентов увеличился (или уменьшился) уровень по сравнению с базисным, принятым за 100 %.
При анализе темпов развития никогда не следует упускать из виду, какие абсолютные величины – уровни и абсолютные приросты – скрываются за темпами роста и прироста. Нужно, в частности, иметь в виду, что при снижении (замедлении) темпов роста и прироста абсолютный прирост может возрастать.
В связи с этим важно изучать еще один показатель динамики – абсолютное значение (содержание) 1 % прироста, который определяется как результат деления абсолютного прироста на соответствующий темп прироста:
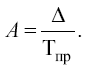
Эта величина показывает, сколько в абсолютном выражении дает каждый процент прироста. Иногда уровни явления за одни годы несопоставимы с уровнями за другие годы из-за территориальных, ведомственных и иных изменений (изменения методологии учета и исчисления показателей и т. п.). Чтобы обеспечить сопоставимость и получить пригодный для анализа временной ряд, нужно произвести прямой пересчет уровней, несопоставимых с другими. Однако иногда нет необходимых для этого данных. В таких случаях можно использовать особый прием, называемый смыканием рядов динамики.
Пусть, например, произошло изменение границ территории, по которой изучалась динамика развития какого-то явления в i-м году. Тогда данные, полученные до этого года, окажутся несопоставимы с данными за последующие годы. Чтобы сомкнуть эти ряды и получить возможность анализа динамики ряда за весь период, примем в каждом из них за базу сравнения уровень i-го года, за который есть данные как в прежних, так и в новых границах территории. Эти два ряда с одинаковой базой сравнения можно затем заменить одним сомкнутым рядом динамики. По данным сомкнутого ряда можно вычислить темпы роста по сравнению с любым годом, можно рассчитать и абсолютные уровни за весь период в новых границах. Тем не менее надо иметь в виду, что результаты, полученные путем смыкания рядов динамики, содержат в себе некоторую погрешность.
Графически динамика явлений наиболее часто изображается в виде столбиковых и линейных диаграмм. Применяются и другие формы диаграмм: фигурные, квадратные, секторные и т. п. Аналитические графики обычно строятся в виде линейных диаграмм
12. Понятие индексов и виды индексов
Важное значение в статистических исследованиях коммерческой деятельности имеет индексный метод. Полученные на основе этого метода показатели используются для характеристики развития анализируемых показателей во времени, по территории, изучения структуры и взаимосвязей, выявления роли факторов в изменении сложных явлений.
Индекс – это относительная величина, показывающая во сколько раз уровень изучаемого явления в данных условиях, отличается от уровня того же явления в других условиях.
Статистический индекс — это относительная величина сравнения сложных совокупностей и отдельных их единиц. При этом под сложной понимается такая статистическая совокупность, отдельные элементы которой непосредственно не подлежат суммированию.
Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям. Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость и достигается единство.
Виды индексов различают по следующим факторам:
§ по степени охвата элементов совокупности:
§ индивидуальные – характеризуют изменение только одного элемента совокупности;
§ сводные (общие) – отражают изменения по всей совокупности элементов сложного явления. Их разновидностью являются групповые индексы.
§ в зависимости от содержания и характера индексируемой величины:
§ индексы количественных показателей (например, индекс физического объема);
§ индексы качественных показателей (например, индекс цен, себестоимости, производительности труда).
§ в зависимости от методологии расчета:
§ агрегатные – могут быть рассчитаны как индексы переменного и постоянного состава;
§ средние из индивидуальных – получаются путем нахождения общих индексов с использованием индивидуальных.
Для удобства восприятия индексов в теории статистики разработана символика:
- q – количество единиц какого-либо вида продукции;
- p – цена единицы какого-либо вида продукции;
- z – себестоимость единицы какого-либо вида продукции;
- t – трудоемкость единицы какого-либо вида продукции
13. Понятие индексного метода и основные виды индексов, используемых в экономических исследованиях.
Индексный метод - метод статистического исследования, позволяющий с помощью индексов соизмерять сложные социально-экономические явления путем приведения анализируемых величин к некоторому общему единству. В роли соизмерителя могут выступать денежная оценка, трудовые затраты и т.п. Метод применяется для изучения динамики явления, позволяет выявлять и измерять влияние факторов на изменение изучаемого явления.
Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям. Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость и достигается единство.
Виды индексов различают по следующим факторам:
по степени охвата элементов совокупности:
индивидуальные – характеризуют изменение только одного элемента совокупности;
сводные (общие) – отражают изменения по всей совокупности элементов сложного явления. Их разновидностью являются групповые индексы.
в зависимости от содержания и характера индексируемой величины:
индексы количественных показателей (например, индекс физического объема);
индексы качественных показателей (например, индекс цен, себестоимости, производительности труда).
в зависимости от методологии расчета:
агрегатные – могут быть рассчитаны как индексы переменного и постоянного состава;
средние из индивидуальных – получаются путем нахождения общих индексов с использованием индивидуальных.
Для удобства восприятия индексов в теории статистики разработана символика:
- q – количество единиц какого-либо вида продукции;
- p – цена единицы какого-либо вида продукции;
- z – себестоимость единицы какого-либо вида продукции;
- t – трудоемкость единицы какого-либо вида продукции
2. Индивидуальные и общие индексы.
Различают следующие индивидуальные индексы:
индекс физического объема – показывает во сколько раз увеличился (уменьшился) объем в натуральных единицах в отчетном периоде по сравнению с базисным
индекс цен – показывает во сколько раз увеличилась (уменьшилась) цена единицы продукции в отчетном периоде по сравнению с базисным;
индекс себестоимости – показывает во сколько раз увеличилась (уменьшилась) себестоимость единицы продукции в отчетном периоде по сравнению с базисным.
Но если необходимо определить общее изменение объема производства или продаж, когда выпускаются различные виды продукции, рассчитывают общие индексы.
Индекс становится общим, когда в расчетной формуле показывается неоднородность изучаемой совокупности. Он может быть рассчитан как агрегатный и как средний из индивидуальных.
Общие индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц, образующих статистическую совокупность и обладают следующими свойствами:
синтетические – посредством индексного метода производится соединение (агрегирование) в целом разнородных единиц статистической совокупности;
аналитические – посредством индексного метода определяется влияние факторов на изменение изучаемого показателя.
3. средние индексы.
Всякий агрегатный индекс может быть преобразован в средний арифметический из индивидуальных индексов. Для этого индексируемая величина отчётного периода, стоящая в числителе агрегатного индекса, заменяется произведением индивидуального индекса на индексируемую величину базисного периода.
4. Индексы структурных сдвигов.
При изучении динамики коммерческой деятельности приходится производить индексные сопоставления более чем за два периода.
Поэтому индексные величины могут определяться как на постоянной, так и на переменной базах сравнения. При этом, если задача анализа состоит в получении характеристик изменения изучаемого явления во всех последующих периодах по сравнению с начальным, то вычисляются базисные индексы. Например, сопоставление объёма розничного товарооборота II, III и IV кварталов с I кварталом.
Но если требуется охарактеризовать последовательно изменения изучаемого явления из периода в период, то вычисляются цепные индексы. Например, при изучении объёма розничного товарооборота по кварталам года сопоставляют товарооборот II квартала c I, III — cо II и IV — с III кварталом.
В зависимости от задачи исследования и характера исходной информации базисные и цепные индексы исчисляются как индивидуальные, так и общие.
Способы расчёта индивидуальных базисных и цепных индексов аналогичны расчёту относительных величин динамики. Общие индексы в зависимости от их вида вычисляются с переменными и постоянными весами — соизмерителями.
Используя индексный ряд за несколько периодов, можно получить динамику стоимости продукции и динамику товарооборота в неизменных ценах, т.е. в ценах какого - то одного прошлого периода. Такие индексные ряды называются индексами с постоянными весами. Для них действует правило: произведение цепных индексов даёт индекс базисный.
Если индексы цен, себестоимости и производительности труда имеют в качестве весов количество продукции отчётного периода, то эти индексы образуют индексные ряды с переменными весами, поскольку в каждом отдельном индексе отчётный период изменяется. Индексы с переменными весами не подчиняются правилу, согласно которому произведение цепных индексов равно базисному.
5. Территориальные индексы
Территориальные индексы представляют собой разновидность относительных величин сравнения, когда сопоставляются сложные показатели, относящиеся к одному и тому же периоду времени, но к разным территориям (городам, районам, областям, государствам). На основе территориальных индексов выполняются международные сопоставления.
Территориальный индекс товарооборота — это отношение суммы выручки от продажи в одном из районов к аналогичному показателю в другом. Один из районов (например, Б) берется за базу сравнения т.е.
Различие объемов товарооборота вызвано различием ассортимента и количества проданных товаров, а также цен.
Условия индексной модели могут нарушаться, хотя и не очень существенно. Использование таких территориальных индексов для анализа абсолютной разницы товарооборотов дает в только приближенный результат.
Территориальные индексы можно также рассчитывать:
с использованием соизмерителей только района А или только района Б;
как среднюю геометрическую из двух территориальных индексов, рассчитанных с разными территориальными весами.
6. Индексы цен.
Индексы цен выполняют роль общего измерителя инфляции в макроэкономических исследованиях и используются для решения следующих задач:
оценка динамики цен на товары производственного и непроизводственного назначения;
для корректировки минимального размера оплаты труда;
для установления ставок налогов;
для обоснования инвестиционных проектов и т.д.
Индекс цен рассчитывается не по всем товарам, а только по товарам представителям, которые составляют товарную корзину. По мере удаления от базисного года эта корзина все менее соответствует по составу и структуре текущему периоду, поэтому состав корзины (а следовательно и весов) должен пересматриваться, особенно в периоды резкого изменения экономических условий. В странах Европы – раз в 5 лет, у нас ежегодно. Увязка индекса, рассчитанного по новым весам, осуществляется с помощью процедуры смыкания динамических рядов.
Различают следующие основные виды индексов цен:
индекс цен Пааше – показывает, во сколько раз товары отчетного периода стали в отчетном же периоде дороже (дешевле), чем в базисном. При этом он имеет тенденцию некоторого занижения темпов инфляции
индекс цен Ласпейреса – показывает, во сколько раз товары базисного периода стали в подорожали (подешевели) из-за изменения цен. При этом он имеет тенденцию некоторого завышения темпов инфляции
индекс потребительских цен (индекс стоимости жизни) – характеризует изменение общего уровня цен на товары и услуги за какой-либо период. Рассчитывается на основе потребительской корзины с недельной, месячной и квартальной периодичностью. Расчет ведется в несколько этапов:
определяются индивидуальные индексы по отдельным товарам и услугам для каждого города;
на их основе и территориальных весов определяются индексы цен тоже отдельных товаров, но по региону (стране). При этом в качестве весов используется численность населения.
На основе этих агрегатных индексов и отдельных весов расходов на приобретение каждого товара потребительских расходов (бюджетов) определяются сводные индексы сначала по группам продовольственных, непродовольственных товаров и услуг, а затем и сводный индекс в целом. А удельный вес расходов определяется по базисному периоду.
индексы дефляторы – используются для пересчета показателей системы национальных счетов из фактических цен в сопоставимые. Дефлятор – коэффициент, переводящий значение стоимостного показателя за отчетный период в стоимостные измерители базисного периода.
14. Агрегатные индексы.
Каждый качественный показатель связан с тем или иным объемным показателем, в расчете на единицу измерения которого он исчисляется (или к единице измерения которого относится). Так, цена единицы товара связана с его количеством (Q); с объемом произведенной продукции связаны такие качественные показатели, как цена (р), себестоимость (z) и трудоемкость (t = T / Q) единицы продукции, а также удельный расход сырья, материалов (m = M / Q).
Сводные индексы качественных показателей должны характеризовать не их изменение вообще применительно к какому-либо произвольному набору товаров или продукции, а изменение цен, себестоимости, трудоемкости или удельных расходов вполне определенного количества произведенной продукции или проданных товаров. Это и достигается путем взвешивания – умножения уровней индексируемого качественного показателя на значения связанного с ним объемного показателя (веса) – и фиксирования весов в числителе и знаменателе индекса на одном и том же уровне. Сопоставление сумм таких произведений дает агрегатный индекс. Аналогично могут быть построены агрегатные индексы динамики себестоимости и трудоемкости единицы продукции, а также индекс удельного расхода сырья или материала.
Основной проблемой при построении этих сводных индексов является экономически обоснованный выбор уровня, на котором нужно зафиксировать веса индекса, т. е. в данном случае объем продукции (или товаров) – Q.
Обычно перед сводным индексом динамики качественного показателя ставится задача измерить не только относительное изменение уровня, но и абсолютную величину того экономического эффекта, который получен в текущем периоде в результате этого изменения: сумму экономии покупателей за счет снижения цен (или сумму их дополнительных расходов, если цены повысились), сумму экономии (или дополнительных затрат) за счет изменения себестоимости и т. п.
Такая постановка задачи приводит к индексам динамики качественных показателей с весами текущего периода:
• во-первых, исследователя интересует изменение себестоимости или трудоемкости той продукции, которая выпущена в настоящее время, а не в прошлом;
• во-вторых, экономический эффект должен быть увязан с фактическими результатами текущего, отчетного, а не предыдущего (базисного) периода.
В качестве примера приведем агрегатный индекс себестоимости:
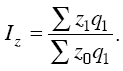
Таким образом, в этом индексе числитель представляет собой сумму фактических затрат на продукцию в отчетном периоде, а знаменатель – условную величину, которая показывает, сколько средств было бы затрачено на продукцию отчетного периода, если бы себестоимость единицы каждого вида продукции сохранялась на базисном уровне.
Реальный экономический эффект, полученный за счет изменения себестоимости единицы продукции, выражается абсолютной величиной, которая вычисляется как разность между суммами в числителе и знаменателе индекса: (? z 1 Q 1?? z 0 Q 1) или (? z 1? z 0 Q 1).
Следовательно, взвешивание по весам отчетного (текущего) периода увязывает индекс качественного показателя с показателем экономического эффекта, который получен за счет изменения индексируемого показателя. Поэтому агре-гатныге индексы! динамики качественный показателей строятся и вычисляются обычно с весами отчетного периода:
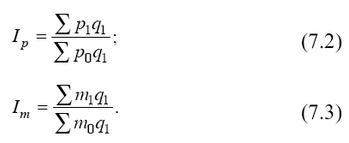
Формула (7.2) представляет собой сводный индекс цен, а формула (7.3) – расчет сводного индекса расхода материалов. В этих индексах разность между числителем и знаменателем характеризует в первом случае уменьшение либо увеличение затрат на приобретение одного и того же набора товаров в зависимости от знака разности; во втором случае – увеличение или уменьшение расхода материалов на производство одного и того же объема продукции.
Задача
Имеются следующие демографические данные по России за 2002-2011 гг.
| Все население на 1.01 млн. чел. | 145,2 | 145,0 | 144,3 | 143,8 | 143,2 | 142,8 | 142,8 | 142,7 | 142,9 | 142,9 |
| Мужчины на 1.01 млн. чел. | 67,6 | 67,5 | 67,0 | 66,7 | 66,3 | 66,0 | 66,0 | 65,9 | 66,1 | 66,1 |
| Женщины на 1.01 млн. чел. | 77,6 | 77,5 | 77,3 | 77,1 | 76,9 | 76,8 | 76,8 | 76,8 | 76,8 | 76,8 |
| Городское на 1.01 млн. чел. | 106,4 | 106,3 | 106,0 | 105,2 | 104,8 | 104,7 | 104,9 | 104,9 | 105,3 | 105,4 |
| Сельское на 1.01 млн. чел. | 38,8 | 38,7 | 38,3 | 38,6 | 38,4 | 38,1 | 37,9 | 37,8 | 37,6 | 37,5 |
| Родилось тыс. чел. | 1397,0 | 1477,3 | 1502,5 | 1457,4 | 1479,6 | 1610,1 | 1717,5 | 1761,7 | 1788,9 | 1796,6 |
| Умерло тыс. чел. | 2332,3 | 2365,8 | 2295,4 | 2303,9 | 2166,7 | 2080,4 | 2081,0 | 2010,5 | 2028.5 | 1925,7 |
| Браки тыс. | 1019,8 | 1091,8 | 979,7 | 1066,4 | 1113,6 | 1262,5 | 1179,0 | 1199,4 | 1215,1 | 1316,0 |
| Разводы тыс. | 853,6 | 798,8 | 635,8 | 604,9 | 640,8 | 685,9 | 703,4 | 699,4 | 639,3 | 669,4 |
Численность населения России на 1.01.2012 – 143,0 млн. чел.; территория РФ 17,1 млн. км2
Рассчитать:
1. Относительные величины структуры:
а) удельный вес мужчин и удельный вес женщин в общей численности населения;
б) удельный вес городского и удельный вес сельского населения в общей численности населения.
2. Относительные величины динамики:
а) числа родившихся – цепным методом; б) числа умерших – базисным методом (к 2002 году).
3. Относительные величины координации:
а) число мужчин на 1000 женщин; б) число разводов на 1000 браков.
4. Относительные величины интенсивности, предварительно рассчитав среднегодовую численность населения
а) рождаемости; б) смертности.
6. Результаты расчетов представить в таблице.
5. Сделать выводы о демографическом состоянии России по результатам расчетов.