Анализ технического задания.

По дисциплине «Информатика»

 

 

Преподаватель: Пряжевская М.В.

Студент: Ксалов Р.М.

Группа: ВМ1-02

 

 

г. Смоленск

2003 г.

Техническое задание.

1. Перевести (тремя способами) заданное число из одной системы счисления в другую по следующей схеме:

 

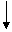
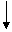
A₁₆ A₈

A₁₀ A₁₀ A₁₀ A₁₀

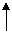
A₂ A₂

 

2. Выполнить действия (двумя способами: в 2 системе счисления и 16 с.с.) над машинными кодами чисел с фиксированной точкой в 16-ти разрядном формате X₁=A+B, X₂=A-B, X₃=-A+B, X₄=-A-B. Произвести проверку.

 

3. Выполнить действия над машинными кодами чисел с плавающей точкой и смешенным порядком в 32-ти разрядном формате Y₁ =C+D, Y₂=C-D, Y₃=-C+D, Y₄=-C-D. Результат Y в 32-ти разрядной двоичной сетке. Произвести проверку.

№ 12
A10	A10	B10	C10	D10
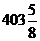
			-512,25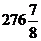

 

Теоретическое введение.

2.1. Системы счисления в ЭВМ

 

В ЭВМ используются позиционные системы счисления: двоичная, восьмеричная шестнадцатеричная и десятичная.

В позиционной системе счисления каждая цифра имеет свой весовой коэффициент , где b – основание системы счисления, i – номер позиции цифры в числе. Общая форма записи чисел в таких системах: . А значение рассчитывается по формуле: .

В ЭВМ используется двоичная система счисления, основание которой равняется 2, и каждая цифра может принимать два значения: 0 и 1. 0000

Кроме двоичной в ЭВМ используется восьмеричная система счисления с основанием 8 (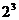) и шестнадцатеричная с основанием 16 ().

Восьмеричная использует цифры: 0, 1, 2, 3, 4, 5, 6, 7.

Шестнадцатеричная использует цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Чтобы перевести целое двоичное число в восьмеричное (шестнадцатеричное), необходимо, двигаясь влево от десятичной точки, делить его на группы по 3 (4) бита. Затем каждая группа заменяется на одну восьмеричную (шестнадцатеричную) цифру. При необходимости к последней группе приписываются нули.

Дробные числа переводятся аналогично, но деление на группы проводится, двигаясь вправо от десятичной точки и записывая недостающие нули, являющиеся значащими.

Для преобразования восьмеричных и шестнадцатеричных чисел в двоичные, необходимо каждую восьмеричную цифру заменить тремя двоичными, шестнадцатеричную – четырьмя.

Преобразование из восьмеричной в шестнадцатеричную возможно с помощью предварительного перевода в двоичную.

Перепишем общую формулу расчёта в позиционной системе счисления в следующем виде

.

Если данную формулу разделить на основание системы счисления b, в остатке получим , а частное примет вид общей формулы, но на одно слагаемое меньше.

Если Q разделить на основание системы счисления, то получим вторую цифру.

 

Общая формула.

Если число в системе C необходимо перевести в систему S, то для этого нужно провести его последовательное деление на основание системы S, выраженное в системе C. На каждом шаге деления получают цифры числа в системе S, начиная с младшей. Процесс деления заканчивается, когда частное станет меньше S.

 

Схема Горнера

.

.

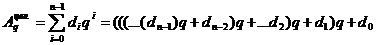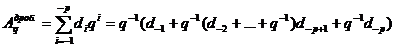Отдельно для целой и дробной части числа в произвольной системе счисления.

При вводе в ЭВМ каждая десятичная цифра заменяется четырьмя двоичными битами. Такая запись десятичных чисел называется двоично-десятичной.

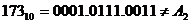- это не двоичный код.

 

Двоичное значение двоично-десятичного числа осуществляется по схеме Горнера.

Аналогично по схеме Горнера можно получить правила перевода дробных чисел из одной системы счисления в другую, но так как там основание системы счисления в отрицательной степени, перевод сводится к ряду последовательных умножений.

Правило1: последовательно умножать переводимое число и полученные дробные части на основание новой системы, выраженное в алфавите исходной, до тех пор, пока дробная часть не станет равной нулю или пока не будет достигнута заданная точность.

Правило2: полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, выразить в алфавите этой системы.

Правило3: записать дробную часть числа в новой системе, начиная с целой части первого произведения.

В частном случае, если знаменатель дробной части представляет целую степень числа, то числитель a переводится как целое b k двоичных бит.

Смешанные числа переводятся по отдельности: целая часть и дробная часть.

Три способа перевода чисел из одной системы счисления в другую:

1) По правилам (триады, тетрады).

2) По степенному ряду.

3) По схеме Горнера.

 

 

2.2. Двоичная арифметика

 

Сложение

 

0+0=0

0+1=1

1+0=1

1+1=0, c_вых = 1

 

X	y

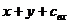
Вычитание

 

0-0=0

0-1=1, b_вых = 1

1-0=1

1-1=0

 

x	Y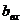

 

В ЭВМ вычитание проводится в виде А-В=А+(-В). Для того отрицаемое слагаемое представляется в дополнительном коде или в коде с дополнением до двух. Чтобы получить дополнительный код двоичного число необходимо проинвертировать его прямой код и к результату прибавить единицу.

При вычитании с помощью прямого кода признаком отрицательного результата является наличие окончательного заёма за пределы разрядной сетки. В этом случае результат получаем в

 

дополнительном коде и для определения его абсолютной величины необходимо перейти к прямому.

При вычитании с помощью дополнительного кода признаком положительного результата является наличие окончательного переноса за пределы разрядной сетки.

Для указания знака числа отводится специальный старший двоичный разряд (или бит). У положительного числа он равен нулю, у отрицательного – единице.

С помощью байта, в котором старший 7-разряд отведён под знак числа, можно представлять числа от –127 до 127.

При сложении двух чисел, в сумме превышающим 127 происходит искажение результата за переполнения разрядной сетки.

Переполнение произошло, если слагаемые имеют одинаковые знаки, а сумма или противоположна.

 

Умножение

 

В начале множимое умножается на младший разряд множителя, получаем первое частичное произведение, затем на второй разряд множителя, получаем второе частичное произведение, но сдвинутое относительно первого на один разряд влево и так далее. Полное произведение получаем суммированием всех частичных.

 

Деление

 

Деление – это последовательное вычитание делителя из делимого, начиная со старших разрядов со сдвигом делителя вправо на один разряд на каждом шаге. На каждом шаге анализируем знак остатка, если он отрицательный, остаток игнорируется, в частное записывается ноль, из делимого снимается следующая цифра, делитель сдвигается на одну позицию вправо.

 

2.3. Формы и форматы представления числовых данных в ЭВМ

 

Естественная форма

 

Естественная форма предназначена для хранения чисел с фиксированной точкой. Для правильных дробей – перед старшим разрядом, для целых чисел – после младшего разряда.

Во всех форматах знак числа занимает место перед старшим разрядом (0 ® +, 1 ® -).

Два формата:

 

Н					…			2 байта
				…
				…

 

 

F					…
				…
				…

 

 

Для сокращения записи можно использовать шестнадцатеричную систему.

 

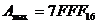
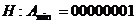
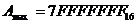
По первой цифре можно определить знак числа. Если оно меньше 8, то число положительное, если больше 8 – отрицательное.

Достоинства форматов: простота и наглядность.

Недостатки: ограниченный диапазон представляемых чисел, возможность переполнения разрядной сетки.

 

Нормальная форма

 

В нормальной форме числа представляются как , где 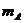– мантисса числа, p – его порядок, q – основание системы счисления.

Для однозначности представления чисел мантисса должна удовлетворять условиям:

Для представления нормальных чисел используются стандартные форматы разной длины. Старший разряд (31) отводится под знак числа, 30 бит отводится под знак порядка, 24-29 – порядок числа, 0-23 – мантисса числа.

 

Знак числа	Знак порядка	Порядок числа ()	Мантисса числа ()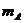
										…

 

Особенности нормальной формы: смещение числовой оси порядков в область положительных значений для облегчения действий над порядками. Не имеющими знака. В формате под порядок отводится 6 бит и седьмой под его знак, следовательно числовая ось лежит в диапазоне

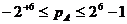
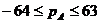
Смещ. порядок, назыв. характеристикой, опред. смещ. порядка вправо на . Если характеристика равн. , то порядок равен нулю, если меньше – порядок отрицательный, если больше – порядок положительный. Если характеристика меньше нуля или больше , произошло переполнение порядка и искажение результатов.

Мантиссы и порядки выраж. в шестнадцатеричной системе счисления в двоичном коде, что позволяет увеличить диапазон представл. чисел в 4 раза.

 

Машинные коды

 

В ЭВМ все арифметические операции сводятся к сложению и сдвигу чисел влево или вправо. При этом учитываются знаки чисел, опред. знак результата и факт наличия и отсутствия переполнения разрядной сетки. Замена вычитания на сложение может проводиться с помощью

 

 

дополнительного и обратного кода. Их суть состоит в том, что отрицательное слагаемое представл. в виде дополнения до

 

некоторой константы K, такой, что K-B>0. Обратный и дополнительный коды отличаются выбором этой константы.

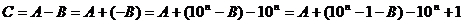, где 10 – основание системы счисления, – const при введении дополнительного, ( -1) – const обратного кода, n – количество разрядов представл. целых чисел в данной системе счисления.

Из полученной суммы необходимо изъять добавленную константу.

В случае дополнительного кода его константа компенсируется ликвидацией ед. переноса из старшего разряда. А в случае обратного кода – ликвидацией единицы и прибавления её к результату, то есть на одну операцию больше. Поэтому для реального вычитания используется дополнительный код, а обратный используется для получения дополнительного.

При сложении чисел с разными знаками единица переноса из старшего разряда является признаком положительного результата, отсутствие переноса – признаком отрицательного результата. При этом код результата находится в дополнительном коде. Чтобы получить его модуль, необходимо скомпенсировать константу дополнительного кода.

При сложении чисел с одинаковыми знаками признаки противоположны. При сложении положительных чисел признаком положительного результата является отсутствие переноса из старшего разряда, признаком отрицательного результата – его наличие. Эти же признаки говорят об отсутствии переполнения разрядной сетки.

Правила построения дополнительного и обратного кода на примере чисел . Старший бит отведён под знак числа.

 

+34
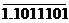
-34	1.0100010	-00100010	-00100010

 

1) Прямой код положительного и отрицательного числа отличаются только знаковыми разрядами.

2) Прямой, дополнительный и обратный коды положительных чисел совпадают.

3) Обратный код отрицательного числа образуется из прямого кода положительного числа путём инверсии кода, включая знаковый разряд.

4) Дополнительный код отрицательного числа образуется дополнением единицы к младшему разряду обратного кода или путём инверсии прямого кода, исключая последнюю единицу и следующие за ней нули.

Числа в естественной форме хранятся в ЭВМ в дополнительном коде, в нормальной форме – в прямом коде.

 

2.5. Действия над числами, представленными в естественной форме

 

1) Числа в естественной форме в памяти хранятся в дополнительном коде.

2) В сумматоре числа складываются вместе со знаками, при этом образуется знак результата.

3) При сложении чисел с разными знаками единица переноса из знакового разряда стирается, то есть компенсируется константа дополнительного кода.

4) При сложении чисел с одинаковыми знаками признаками переполнения разрядной сетки являются:

- знак суммы не соответствует знакам слагаемых;

- переносы из старшего разряда суммы в знаковый и из знакового за пределы разрядной сетки не согласуются.

 

2.6. Действия над числами, представленными в нормальной форме

 

 

1) Числа в нормальной форме хранятся в памяти в прямом коде с нормализованными мантиссами.

2) Сложение чисел проводится путём сложения их мантисс при одинаковых характеристиках слагаемых. За общий выбирается наибольший порядок. Выравнивание порядков слагаемых проводится путём сдвига вправо мантиссы меньшего числа.

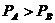
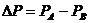
3) При сложении мантисс с одинаковыми знаками возможно переполнение разрядной сетки, что будет являться нарушением нормализации влево. Для его устранения необходим сдвиг мантиссы на один разряд вправо и соответ. увелич. характ. на 1.

4) Результаты в прямом коде нормализуются.

5) Действия в сумматоре выполняются над кодами мантисс, которые поступают из регистров в младшие 24 бита сумматора, знаки мантисс и характеристики заносятся в специальные схемы, которые обеспечивают выравнивание характ., норм. мантиссы рез., формирование знака результата и характеристики результата. Старшие разряды сумматора 24-31 заполняются нулями.

6) Алгоритмы сложения после выравнивания характеристик зависят от знаков слагаемых:

- если знаки одинаковые, модули мантисс (прямые коды) суммируются. Переполнение определяется наличием переноса единицы из старшего разряда мантиссы в 24 бит, что вызывает нарушение нормализации мантиссы влево. Нормализация проводится сдвигом на одну шестнадцатую вправо. Старшая тетрада мантиссы заполняется кодом 0001. Характеристика результата увеличивается на 1. В регистре результата сумматора форм. рез. операции:

схема анализа знака и характеристик

В 31-й заносят знак результата. В 30-24 – характеристика. 23-0 – мантисса в прямом коде;

- если знаки слагаемых различны, отрицательная мантисса преобразуется в дополнительный код и мантиссы суммируются. Признаком положительного результата является перенос из старшего разряда мантиссы в младший характеристики, кот. стирается. Признаком отрицательного результата – его отсутствие. При этом мантисса представляется в дополнительном коде и должна быть преобразована в прямой. При сложении чисел с разными знаками возможно нарушение нормализации мантиссы вправо, тогда старшая 16-ая цифра мантиссы равна нулю. Нормализацию проводят сдвигом на 16-ую цифру влево и уменьшением характеристики на 1. После этого в регистре форм. результат. Знаковый разряд заносят в знаковый разряд большего по модулю слагаемого.

 

Анализ технического задания.

1. Перевести заданное число из одной системы счисления в другую можно следующими тремя способам:

1) По правилам (триады, тетрады).

2) По степенному ряду.

3) По схеме Горнера.

 

2. Чтобы выполнить действия над машинными кодами чисел с фиксированной точкой в 16-ти разрядном формате (двумя способами: в 2 системе счисления и 16 с.с.) X₁=A+B, X₂=A-B, X₃=-A+B, X₄=-A-B, переведём заданные числа в двоичную и шестнадцатеричную системы счисления. Затем найдём А_пк, В_пк, А_дк, В_дк. Выполним требуемые операции. Произведём проверку.

 

3. Чтобы выполнить действия над машинными кодами чисел с плавающей точкой и смешенным порядком в 32-ти разрядном формате Y₁ =C+D, Y₂=C-D, Y₃=-C+D, Y₄=-C-D (результат Y в 32-ти разрядной двоичной сетке), переведём заданные числа в шестнадцатеричную систему счисления. Затем найдём А_пк, В_пк, А_дк, В_дк. Выполним требуемые операции. Произведём проверку.

 

 

Ход работы

Задание 1

A₁₀®A₂

 

а) Переведем целую часть в двоичную систему счисления. Для этого воспользуемся правилом деления на основание системы счисления.

 

_ 403| 2 __

402 201| 2 __

1 200 100| 2 __

1 100 50| 2 __

0 50 25| 2 __

0 24 12| 2 _

1 12 6| 2 _

0 6 3| 2 _

0 2| 1

 

403₁₀ = 110010011₂

Переведем дробную часть в двоичную систему счисления. Для этого воспользуемся правилом умножения на основание системы счисления.

Так как , то

Итак, A₂ = 110010011,101.

 

б) Воспользуемся разложением по степенному ряду.

A₁₀ = = 256 +128+16+2+1+ + 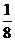= 2⁸ + 2⁷ + 2⁴ + 2¹ + 2⁰ + 2^-1 + 2^-3 = 110010011.101₂ = A₂.

Итак, A₂ = 110010011,101.

 

в) Воспользуемся схемой Горнера.

= 403,0625₁₀ = (0100×1010 + 0000)×1010 + 0011 + (((0101×1010^-1 + 0010)×1010^-1 + 0110)×1010^-1 + 0000)×1010^-1 = 110010011,101₂

Итак, A₂ = 110010011,101.

 

 

А₁₀®А₁₆

 

а) Воспользуемся разложением по степенному ряду.

A₁₀ = = 256 + 9×16 + 3 + 10×16^-1 = 16² + 9×16 + 3×16⁰ + 10×16^-1 = 193,A₁₆ = A₁₆.

Итак, A₁₆ = 193,A

 

б) Воспользуемся правилами умножения и деления на основание системы счисления.

Переведем целую часть в шестнадцатеричную систему счисления.

 

 

_ 403| 16_

400 25| 16

3 16 1

 

 

403₁₀ = 193₁₆

Переведем дробную часть в двоичную систему счисления.

 

0,625

´ 16

10,000

 

0,625₁₀ = 0,A₁₆

Итак, A₁₆ = 193,A.

 

в) Воспользуемся схемой Горнера.

403,0625₁₀ = (4×A + 0)×A + 3×A + 0 + (((5×A^-1 + 2)×A^-1 + 6)×A^-1 + 0)×A^-1 = 193,A₁₆.

Итак, A₁₆ = 193,A.

 

А₁₆®А₂

 

а) Воспользуемся разложением по степенному ряду.

A₁₆ = 193,A = 1×16² + 9×16¹ + 3×16⁰ + A×16^-1 = 2⁸ + (2³ + 1) ×2⁴ + (2 + 1) ×2⁰ + (2³ + 2) ×2^-3 = 2⁸ + 2⁷ + 2⁴ + 2¹ + 2⁰ + 2^-1 + 2^-3 = 110010011,101₂ = A₂.

Итак, A₂ = 110010011,101.

 

б) Воспользуемся правилом тетрады.

A₁₆ = 193,A = 0001’1001’0011.1010₂ = 110010011,101₂ = A₂.

Итак, A₂ = 110010011,101.

 

в) Воспользуемся правилами умножения и деления на основание системы счисления.

Переведем целую часть в двоичную систему счисления.

 

_ 193| 2___

192 C9| 2___

1 C8 64| 2__

1 64 32| 2__

0 32 19| 2__

0 18 C| 2_

1 C 6| 2__

0 6 3| 2_

0 2 |1

 

193₁₆ = 110010011₂

Переведем дробную часть в двоичную систему счисления.

 

0,A

´ 2

1,4

´ 2

0,8

´ 2

1,0

 

0,A₁₆ = 0,101₂

 

Итак, A₂ = 110010011,101.

 

A₁₆ ® A₁₀

а) Воспользуемся разложением по степенному ряду.

A₁₆ = 193,A = 1×16² + 9×16¹ + 3×16⁰ + A×16^-1 = 256 + 9×16 + 3 + 10×16^-1 = = A₁₀.

Итак, A₁₀ = .

б) Воспользуемся правилами умножения и деления на основание системы счисления.

Переведем целую часть в десятичную систему счисления.

 

_ 193| A__

190 28| A_

3 28 4

 

193₁₆ = 403₁₀

Переведем дробную часть в десятичную систему счисления.

 

0,A

´ A

6,4

´ A

2,8

´ A

5,0

 

0,A₁₆ = 0,625₁₀

Итак, A₁₀ = 403,625 = .

в) Воспользуемся схемой Горнера.

A₁₆ = 193,A = ((1×16 + 9)×16 + 3 + 10×16^-1 = 403,625 =

Итак, A₁₀ = 403,625 = .

 

А₂®А₁₀

 

а) Воспользуемся разложением по степенному ряду.

A₂ = 110010011,101 = 2⁸ + 2⁷ + 2⁴ + 2¹ + 2⁰ + 2^-1 + 2^-3 = 256 +128+16+2+1+ + 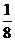= = A₁₀.

 

Итак, A₁₀ = .

 

б)Воспользуемся схемой Горнера.

A₂ = 110010011,101₂ = (((((((1×2+1) ×2+0) ×2+0) ×2+1) ×2+0) ×2+0) ×2+1) ×2+1+((1×2^-1+0) ×2^-1+1) ×2^-1 = = A_{10 .}

Итак, A₁₀ = .

 

в) Воспользуемся правилами умножения и деления на основание системы счисления.

Переведем целую часть в десятичную систему счисления.

 

_ 110010011| 1010__

110010000 101000| 1010

11 101000 |100

 

110010011₂ = 403₁₀

Переведем дробную часть в десятичную систему счисления.

 

0,101

´ 1010

101

110,010

´ 1010

010

010,100

´ 1010

0100

101,000

 

0,101₂ = 0,625₁₀

Итак, A₁₀ = .

 

A₁₀ ® A₈

а) Воспользуемся правилами умножения и деления на основание системы счисления.

Переведем целую часть в двоичную систему счисления.

_ 403| 8 __

400 50| 8 _

3 48 6

 

403₁₀ = 623₈

Переведем дробную часть в двоичную систему счисления.

 

 

0.625

_ _´8

5,000

 

Итак, A₈ = 623.5.

 

б) Воспользуемся разложением по степенному ряду.

A₁₀ = = 6×8² + 2×8¹ + 3×8⁰ + 5×8^-1 = 623.5₈ = A₈.

Итак, A₈ = 623.5.

 

в) Воспользуемся схемой Горнера.

A₁₀ = = 403,625 = (4×12 + 0)×12 + 3 + ((5×12^-1 + 2)×12^-1 + 6)×12^-1 = 623.5₈ = A₈.

Итак, A₈ = 623.5.

 

A₈ ® А₂

 

а) Воспользуемся правилом триады.

A₈ = 623.5₈ = 110’010’011.101₂ = 110010011.101₂ = A₂.

Итак, A₂ = 110010011,101.

 

б) Воспользуемся правилами умножения и деления на основание системы счисления.

Переведем целую часть в двоичную систему счисления.

_ 623| 2___

622 311| 2___

1 310 144| 2__

1 144 62| 2__

0 62 31| 2__

0 30 14| 2_

1 14 6| 2_

0 6 3| 2_

0 2 1

 

623₈ = 110010011₂

Переведем дробную часть в двоичную систему счисления.

 

0.5

´ 2

1.2

´ 2

0.4

´ 2

1,0

 

0,5₈ = 0,101₂

Итак, A₂ = 110010011,101.

 

в) Воспользуемся разложением по степенному ряду.

A₈ = 623.5₈ = 6×8² + 2×8¹ + 3×8⁰ + 5×8^-1 = (2² + 2) ×8² + 2⁴ + 2¹ + 2⁰ + (2² + 2⁰) ×8^-1 = 2⁸ + 2⁷ + 2⁴ + 2¹ + 2⁰ + 2^-1 + 2^-3 = 110010011,101₂ = A₂.

Итак, A₂ = 110010011,101.

A₈ ® A₁₀

а) Воспользуемся разложением по степенному ряду.

A₈ = 623.5₈ = 6×8² + 2×8¹ + 3×8⁰ + 5×8^-1 = = A₁₀

Итак, A₁₀ = .

 

б) Воспользуемся правилами умножения и деления на основание системы счисления.

Переведем целую часть в десятичную систему счисления.

_ 623| 12_

620 50| 12

3 50 4

 

623₈ = 403₁₀

Переведем дробную часть в десятичную систему счисления.

 

0,5

´ 12

6,2

´ 12

2,4

´ 12

5,0

 

0,5₈ = 0,625₁₀

Итак, A₁₀ = .

 

в)Воспользуемся схемой Горнера.

A₈ = 623.5₈ = (6×8+2)×8+3+8^-1×5 = = A₁₀

Итак, A₁₀ = .

 

Задание 2

Переведем числа 268 и -368 в двоичную и шестнадцатеричную системы счисления.

 

_ 268| 2 __

268 134| 2 __

0 134 67| 2 __

0 66 33| 2 _

1 32 16| 2 _

1 16 8| 2 _

0 8 4| 2 _

0 4 2| 2 _

0 2 1

 

268₁₀ = 100001100₂ = 10C₁₆

_ 368| 2 __

368 184| 2 __

0 184 92| 2 __

0 92 46| 2 _

0 46 23| 2 _

0 22 11| 2 _

1 10 5| 2 _

1 4 2| 2 _

1 2 1

-368₁₀ = -101110000₂ = -170₁₆

 

A_пк = 0000000100001100₂ = 010C₁₆

B_пк = 0000000101110000₂ = 0170₁₆

 

Найдем A_дк и B_дк.

 

₊ 1111111011110011

_______________ 1

A_дк =1111111011110100

 

₊ 1111111010001111

_______________ 1

B_дк =1111111010010000

 

A_дк = 1111111011110100₂ = FEF4₁₆

B_дк = 1111111010010000₂ = FE90₁₆

 

1) X₁ = A + B = A_пк + B_дк – сложение чисел с разными знаками.

 

A_пк = 0000000100001100

B_дк = 1111111010010000

A_пк = 010C

B_дк = FE90

FF9C

 

 

Перенос в старший разряд отсутствует, следовательно, результат отрицательный, в дополнительном коде.

 

1111111110011100 FF9C

1 1

1111111110011101 FF9B

0000000001100100 0064

 

|X₁ | = 0000000001100100 = 0064₁₆, X₁< 0.

Проверка. X₁ = A + B = 268₁₀ – 368₁₀ = -100₁₀.

|X₁ | = 100₁₀ = 64 + 32 + 4 = 2⁶ + 2⁵ + 2² = 1100100₂ = 64₁₆.

 

2) X₂ = A – B = A_пк + B_пк – сложение чисел с одинаковыми знаками.

 

A_пк = 0000000100001100

B_пк = 0000000101110000

*)0000001001111100

A_пк = 010С

B_пк = 0170

*)027С

 

Перенос за пределы разрядной сетки отсутствует, следовательно, результат положительный, в прямом коде.

X₂ = 0000001001111100₂ = 027С₁₆

Проверка. X₂ = A - B = 268₁₀ + 368₁₀ = 636₁₀.

X₂ = 636₁₀ = 512 + 64 + 32 + 16 + 8 + 4 = 2⁹ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2² = 1001111100₂ = 27С₁₆.

 

3) X₃ = – A + B = A_дк + B_дк – сложение чисел с одинаковыми знаками.

 

A_дк = 1111111011110100

B_дк = 1111111010010000

1)1111110110000100

A_дк = FEF4

B_дк = FE90

1)FD84

 

Перенос в старший разряд, следовательно, результат отрицательный, в дополнительном коде.

 

1111110110000100 FD84

1 1

1111110110000011 FD83

0000001001111100 027C

 

|X₃| = 0000001001111100₂ = 027C₁₆, X₃< 0.

Проверка. X₃ = - A + B = - 268₁₀ - 368₁₀ = -636₁₀.

|X₃| = 636₁₀ = 512 + 64 + 32 + 16 + 8 + 4 = 2⁹ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2² = 1001111100₂ = 27С₁₆.

 

4) X₄ = – A – B = A_дк + B_пк– сложение чисел с разными знаками.

 

A_дк = 1111111011110100

B_пк = 0000000101110000

1)0000000001100100

A_дк = FEF4

B_пк = 0170

1)0064

 

Перенос в старший разряд, следовательно, результат положительный, в прямом коде.

X₄ = 0000000001100100₂ = 0064₁₆

Проверка. X₄ = - A - B = - 268₁₀ + 368₁₀ = 100₁₀.

X₄ = 100₁₀ = 64 + 32 + 4 = 2⁶ + 2⁵ + 2² = 1100100₂ = 64₁₆.

 

Задание 3

 

Переведем числа - 512,25 и 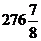в шестнадцатеричную систему счисления.

512₁₀ = 2×256 = 2×16² = 200₁₆

0,25 = 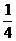= = 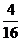0,4₁₆

C₁₆ = -200,4.

m_Cпк =0,2004; p_C = 40+3 = 43;

 

биты: 31 30 29 28 27 26 25 24|23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

С: 1 1 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0

 

C®C3200400.

 

276₁₀ = 256 + 16 + 4 = 16² + 16¹ + 4×16⁰ = 114₁₆

= = 0,E₁₆

D₁₆ =114,E.

m_Dпк = 0,114E; p_D = 40+3 = 43;

биты: 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

D: 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 1 0 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0

 

D®43114E00.

 

Найдём дополнительные коды мантисс.

m_Cпк = 1,0000 – 0,2004 = 0,DFFC

m_Dпк = 1,0000 – 0,114E = 0,EEB2

 

1) Y₁ = C+D, C<0, D>0. Y₁ = C_дк + D_пк

 

m_Cдк = 00’DFFC00 p_C = 43

+

m_Dпк = 00’114E00 p_D = 43

m_Y1дк = 00’F14A00 p_Y1 = 43

 

Переноса нет, следовательно результат отрицательный, в дополнительном коде.

 

1,0000

0,F14A

m_Y1пк = 0,0EB6

 

Нарушения нормализации мантиссы не произошло.

m_Y1 = 00’EB6000 p_Y1 = 43 -1 = 42 Y₁ = - EB,6

Y₁ ® C2EB6000

Y₁ ®11000010111010110110000000000000

Проверка.

Y₁ = - 512,25 + 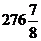= -512,25 + 276,875 = -235,375.

235₁₀ = 15×16 + 11 = EB₁₆

0,375₁₀

Поделиться: