Связь между количественными признаками измеряется через их вариацию. Измерить зависимость (связь) между двумя коррелирующими величинами – значит определить, насколько вариация результативного признака обусловлена вариацией факторного признака.
В качестве показателей тесноты связи между количественными признаками наиболее часто используются линейный коэффициент корреляции, коэффициенты корреляции рангов, эмпирическое корреляционное отношение, теоретическое корреляционное отношение, коэффициент Фехнера.
Линейный коэффициент корреляции
Линейный коэффициент корреляции применим лишь в случае линейной зависимости между признаками.
Если форма связи между х и у не определена, его рассчитывают с целью получить ответ на вопрос, можно ли считать зависимость линейной.
Линейный коэффициент корреляции может быть построен на основе отклонений индивидуальных значений х и у от соответствующей средней величины, причем учитываются не только знаки, но и значения отклонений (
) и (
) (ср. с коэффициентом Фехнера), выраженные для сопоставимости в единицах среднего квадратического отклонения каждого признака, т.е. как нормированные отклонения t:
и 
,
где 
, 
– соответственно среднее квадратическое отклонение в ряду х и у.
Линейный коэффициент корреляции представляет собой среднюю величину из произведений нормированных отклонений для х и у:
(1)
или
. (2)
Величина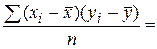 
называется ковариацией, поэтому другое определение r такое:
Линейный коэффициент корреляции представляет собой частное от деления ковариации между х и у на произведение их средних квадратических отклонений.
В литературе встречаются и другие формы записи формулы для r; все они получены путем соответствующих несложных преобразований формулы (1). Эти формулы, в частности, следующие:
, (1, а)
, (1, б)
, (1, в)
, (1, г)
где 
– коэффициент регрессии в уравнении связи.
Линейный коэффициент корреляции может принимать следующие значения:
, (13)
причем знак определяется в ходе решения (см. (11,а)):
а) 
> 
, то r имеет знак «+» – прямая связь между х и у;
б) < , то r имеет знак «– » – обратная связь между х и у;
в) = , то r =0, что означает в одних случаях отсутствие связи между х и у,в других случаях – отсутствие линейной взаимосвязи между х и у;
г) | r | = 1 – функциональная зависимость между х и у (следовательно всякое промежуточное значение | r | от 0 до 1 характеризует степень приближения корреляционной связи между х и у к функциональной).
Проверка коэффициента корреляции на значимость (существенность).
1) n > 50.
Вычисляется средняя ошибка коэффициента корреляции:
, (4)
если 
, то r считается значимым (существенным), а связь – реальной.
При вероятности 0,997, для которой коэффициент доверия t =3, доверительные границы r составят:
.
2) n < 30.
А. Вычисляется средняя ошибка коэффициента корреляции (при n < 30):
(4)
и значимость r проверяется на основе t -критерия Стьюдента. При этом выдвигается и проверяется нуль-гипотеза 
о равенстве r нулю, т.е. об отсутствии связи между х и у в генеральной совокупности.
Б. Определяется расчетное значение критерия:
. (5)
В. Из таблиц с заданными параметрами (с уровнем значимости 
= 0,05 и числом степеней свободы 
= n – 2) находят 
.
Г. Сопоставляют 
с :
– если > , то нулевая гипотеза отвергается и линейный коэффициент r считается значимым, а связь между х и у – реальной;
– если < , то нулевая гипотеза не отвергается и линейный коэффициент r считается незначимым, т.е. считается, что связь между х и у отсутствует, и значение r, отличное от нуля, получено случайно.
Коэффициенты корреляции рангов
Наряду с линейным коэффициентом корреляции r для измерения тесноты связи между двумя коррелируемыми признаками используются менее точные, но более простые по расчету непараметрические показатели: коэффициент Фехнера, коэффициенты корреляции рангов (или ранговые коэффициенты корреляции) Спирмэна 
и Кендэла 
, которые основаны на корреляции не самих значений коррелируемых признаков, а их рангов.
Ранг – это порядковый номер, присваиваемый каждому индивидуальному значению х и у (отдельно) в ранжированном ряду.
Ранжирование – это процедура упорядочения объектов изучения, которая выполняется на основе предпочтения.
Правила ранжирования:
– оба признака необходимо ранжировать (нумеровать) в одном и том же порядке: от меньших значений к большим (и наоборот);
– если встречается несколько одинаковых значений х (или у), то каждому из них присваивается ранг, равный частному от деления суммы рангов (суммы мест), приходящихся на это значение, на число равных значений (например, если за рангом 3 следуют три равных значений признака, то им всем присвоится ранг 5, т.к. (4 + 5 + 6) / 3 = 5);
– ранги признаков х и у обозначаются символами 
и 
(иногда 
и 
).
Суждение о связи между изменениями значений х и у основано на сравнении поведения рангов по двум признакам параллельно:
– если у каждой пары х и у ранги совпадают, это характеризует максимально тесную прямую связь;
– если же наблюдается полная противоположность рангов, т.е. в одном ряду ранги возрастают от 1 до n, а в другом – убывают от n до 1, это максимально возможная обратная связь.
Коэффициент корреляции рангов Спирмэна (
) (применяется обычно на начальном этапе выявления связи между изучаемыми показателями и может быть использован для определения связи как между количественными, так и между качественными признаками при условии, если их значения можно упорядочить или проранжировать).
Коэффициент Спирмэна рассчитывается так:
– значения признаков х и у нумеруют (отдельно) в порядке возрастания от 1 до n, т.е. им присваивают определенный ранг ( и 
) – порядковый номер в ранжированном ряду;
– для каждой пары рангов находят их разность d = – ;
– вычисляют квадраты этих разностей 
;
– вычисляют коэффициент корреляции рангов Спирмэна по одной из формул
или 
. (6)
Коэффициент корреляции рангов Спирмэна может принимать следующие значения:
(7)
(ср. с r). Следует иметь в виду, что, поскольку коэффициент Спирмэна учитывает разность только рангов, он менее точен по сравнению r. Поэтому его крайние значения (1 или 0) нельзя безоговорочно расценивать как свидетельство функциональной связи или полного отсутствия зависимости между х и у.
Коэффициент корреляции рангов Кендэла (
) (может быть использован для определения связи как между количественными, так и между качественными признаками, характеризующими однородные объекты, ранжированные по одному признаку).
или 
, (8)
где S – сумма положительных и отрицательных баллов.
Расчет коэффициента выполняется в следующей последовательности:
1) Ранги х (и ) располагаются строго в порядке возрастания.
2) Значения у располагаются в порядке, соответствующем значениям х.
3) Параллельно записывают соответствующее каждому значению значение (см. пример к вычислению коэффициента ).
4) Устанавливается мера соответствия последовательности 
«правильному» следованию (напоминаем, расположены строго по возрастанию):
а) для каждого последовательно определяют число следующих за ним рангов, превышающих его значение, т.е. определяют «правильное» следование, и они учитываются со знаком «+», а их сумма обозначается буквой P;
б) для каждого последовательно определяют число следующих за ним рангов, меньших по значению, т.е. определяют «неправильное» следование, и они учитываются со знаком «–», а их сумма обозначается буквой Q.
5) Определяется сумма баллов по всем членам ряда, т.е. S=P+Q.
6) Вычисляется по (18).
Преимущества коэффициентов корреляции рангов Спирмэна 
и Кендэла 
:
· они легко вычисляются;
· могут быть использован для определения связи как между количественными, так и между качественными признаками;
· не требуется знать форму связи изучаемых явлений.
Коэффициент конкордации (W – множественный коэффициент ранговой корреляции) применяется в тех случаях, когда число ранжируемых признаков (факторов) больше двух и вычисляется по следующей формуле
, (9)
где S – сумма квадратов отклонений суммы m рангов от их средней
величины;
m – число ранжируемых признаков;
n – число ранжируемых единиц (число наблюдений).
Коэффициент конкордации W может принимать следующие значения:
; (10)
применяется особенно часто в экспертных оценках, например, для того, чтобы определить степень согласованности мнений экспертов о важности того или иного оцениваемого показателя или составить рейтинг отдельных единиц по какому-либо признаку.
Практическая часть
1. Решить задачу:
Имеются данные об объеме основных фондов по 30 промышленным предприятиям, млн. руб.: 380, 320, 290, 240, 320, 210, 245, 350, 250, 200, 308, 475, 274, 382, 290, 385, 465, 485, 476, 464, 378, 240, 262, 212, 215, 258, 185, 192, 201, 185.
Представьте эти данные в сгруппированном виде, объединив предприятия в группы по размеру основных фондов, указав по каждой группе число предприятий.
Решение.
Определим число интервалов по формуле Стреджесса 
групп с равными интервалами.
Определим величину интервала группировки 
млн.руб.
Тогда группировка предприятий по величине основных фондов имеет вид:
| Объем основных фондов, млн.руб. | Число предприятий |
| 185-235 | |
| 235-285 | |
| 285-335 | |
| 335-385 | |
| 385-435 | |
| 435-485 | |
| Итого |
2. Решить задачу:
По приведенным в таблице данным рассчитайте относительные величины интенсивности и сравнения.
| Показатели | Район 1 | Район 2 |
| Численность населения, тыс. чел. | 150,0 | 200,0 |
| Производство обуви, тыс. пар | 420,0 | 450,0 |
Решение.
Относительная величина интенсивности (показатель интенсивности, эффективности) — характеризует степень распространения одного явления в среде другого явления.
Рассчитаем относительную величину интенсивности – производство обуви на 1 человека.
По району 1: 
пар на 1 чел.
По району 2: 
пар на 1 чел.
Относительная величина сравнения (показатель сравнения) — характеризует соотношение между разными совокупностями по одноименным показателям.
Рассчитаем относительные величины сравнения численности населения и производства обуви во втором районе по сравнению с первым.
По численности населения: 
, т.е. численность населения второго района в 1,33 раза больше численности населения второго района.
По производству обуви: 
, т.е. производство обуви второго района в 1,07 раза больше производства обуви второго района.
3. Решить задачу:
В 2017 году численность персонала составила 1380 чел., в 2016 году 1200 чел. Рассчитать темп роста и темп прироста численности персонала.
Решение.
Темп роста = Показатель отчетного периода ∙ 100% / Показатель базисного периода = 
.
Темп прироста = Темп роста – 100% = 
.