Преобразование структурных схем.

Контрольная работа

по дисциплине: «Основы теории управления»

 

 

Исполнитель:

студент группы 8153-21

заочное отделение

№ зачетной книжки 815613

Валиахметов И.Р.

 

Руководитель:

Ягьеева Л.Т.

 

 

Казань, 2018

Содержание

Введение……………………………………………………………………....3

1. Структурная схема АС.........................................................................4

2. Преобразование структурных схем.....................................................5

2.1. Последовательность соединения звеньев..........................................5

2.2. Правила преобразования структурных схем………………………..6

3. Графические метод преобразования структурных схем…………10

4. Методы оценки качества регулирования…………………………….11

4.1. Критериев качества регулирования разделяют…………………….11

5. Коэффициенты ошибок………………………………………………13

Заключение………………………………………………………..........…15

Список использованной литературы……………………………....…...16

 

 

Введение

Структурной схемой системы называется графическое изображение показывающее, из каких элементов состоит система, и каким образом они соединены между собой.

Структурная схема представляет собой математическую модель состоящую из совокупности типовых динамических звеньев, и является очень удобным, информативным и наглядным способом представления системы. необходимо знать математическое описание системы в виде ее общей передаточной функции. Структурные схемы позволяют достаточно просто решить эту проблему путем сворачивания всей совокупности типовых динамических звеньев в одно динамическое звено. Для этого применяются три правила преобразования структурных схем и правила переноса узла и сумматора

В соответствии со структурной схемой всегда можно записать передаточную функцию системы и ее дифференциальное уравнение.

Реальные объекты обладают сложной структурой. Для определения передаточных функций сложных объектов используют упрощение их структурных схем с помощью трех основных типов соединений.

Критерий правильности упрощения схемы заключается в равенстве входных и выходных сигналов упрощаемого участка до и после преобразования.

 

 

Структурная схемы АС

Систему управления можно разбить на блоки, имеющие вход и выход(объект, регулятор, привод, измерительная система). Для того, чтобы показать взаимосвязи этих блоков, используют структурные схемы.
При составлении структурных схем каждое звено системы (группа звеньев) обозначается прямоугольником, в который вписывается его передаточная функция.

Рисунок 1– Операторная запись и запись в изображениях Лапласа

 

Решение большинства задач теории автоматического управления, основано на использовании математических моделей исследуемых систем.

Схема системы, представленная в виде совокупности (соединения) всех её элементов представленных передаточными функциями, называется структурной схемой системы.

Для суммирующих элементов используют специальное обозначение– круг, разбитый на сектора. Если сектор залит черным цветом, поступающий в него сигнал вычитается, а не складывается с другими. Разветвление сигнала обозначается точкой, как и радиотехнике.

Преобразование структурных схем.

Поскольку исследуемый объект в целях упрощения анализа функционирования разбит нами на звенья, то после определения передаточных функций для каждого звена встает задача объединения их в одну передаточную функцию объекта.

2.1Последовательность соединения звеньев:

1) Последовательное соединение.
При последовательном соединении звеньев их передаточные функции перемножаются.

2) Параллельное соединение.

При параллельном соединении звеньев их передаточные функции складываются.

3) Обратная связь (цепь по ходу сигнала (от точки приложения входной переменной до точки съема выходной переменной) называется прямой цепью, против хода сигнала (от выхода к входу)– обратной цепью):
- отрицательная

2.2 Основные правила преобразования структурных схем.

1. Группу последовательного, параллельного соединения звеньев или охваченных обратной связью соединения звеньев можно заменить одним звеном с соответствующей передаточной функцией.

2. Точку приложения или съема воздействия можно переносить через одно или несколько звеньев, добавляя в преобразуемую цепь звено с такой передаточной функцией, чтобы выходной сигнал этой цепи не изменился.

 

№	Операция	Исходная схема	Преобразованная схема
	Перестановка узлов разветвления
	Перестановка сумматоров
	Перенос узла разветвления через звено вперед
	Перенос узла разветвления через звено назад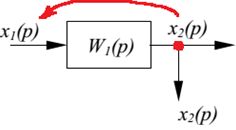
	Перенос сумматора через звено вперед
	Перенос сумматора через звено назад

 

 

Пример, структурной схемы линейной непрерывной системы:

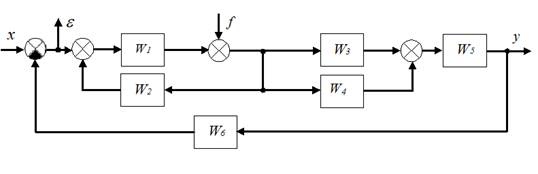
На приведенной схеме стрелками с буквами показаны входные и выходные сигналы относительно которых, можно получить передаточные функции исходной системы.

Например:

 

y

1) Wху -?

 

2) Wfy -?

 

3) Wx -?

 

 

4) Wf -?

 

Указанные передаточные функции системы позволяют установить математические зависимости между соответствующими входными и выходными сигналами.

1

При преобразовании структурных схем используются следующие правила.

1) Объединение последовательно соединенных звеньев:

x y

 

x y Wэкв =

 

2) Объединение параллельно соединённых звеньев:

 

 

Wэкв =

 

3) Замыкание звена обратной связью:

x y

 

«+» - при отрицательной обратной связи

 

«–» - при положительной обратной связи

 

4) Приведение ОС к единичной:

y

x

W1

 

 

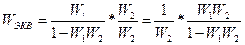
5) Перенос точки съёма через линейное звено против хода сигнала:

		y
	x		y

W

W

x

 

6) Перенос точки съёма через линейное звено по ходу сигнала:

	y

y

W

W

x y x

x

1/W

x

 

y

7) Перенос сумматора через линейное звено против хода сигнала:

		y
	x
			W
		W

 

x

 

y = x·W + x₁ y= (x+x₁·1/W)·W = xW + x₁

 

 

8) Перенос сумматора через линейное звено по ходу сигнала: