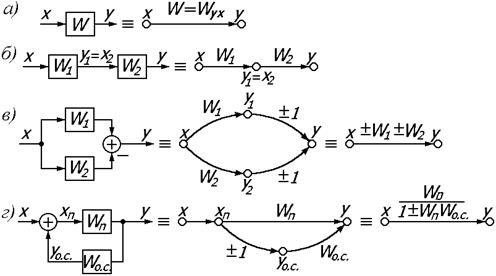
Информация о структуре системы и передаточных свойствах ее элементов может быть задана не только в виде обычной алгоритмической схемы, но и в виде сигнального графа.
Сигнальный граф системы управления представляет собой ориентированный граф – совокупность дуг, изображающих отдельные звенья и указывающих направление передачи сигнала, и вершин, соответствующих входным и выходным сигналам звеньев. Отдельному звену алгоритмической схемы, изображаемому прямоугольником, на сигнальном графе системы соответствует стрелка, соединяющая вершины х и у. Около стрелки указывается передаточная функция звена. Если к вершине подходят несколько дуг, то соответствующий ей сигнал равен сумме всех выходных сигналов этих дуг. Если из вершины исходят несколько дуг, то входные сигналы всех дуг одинаковы и равны сигналу данной вершины.
Методы оценки качества регулирования.
Качество любой системы регулирования определяется величиной ошибки:
x (t)= g (t)− y (t)=Φ x (p) g (t)
Но функцию ошибки x (t) для любого момента времени трудно определить, поскольку она описывается с помощью ДУ системы – Φ x (p) – высокого порядка, и зависит от большого количества параметров системы. Поэтому оценивают качество САР по некоторым ее свойствам, определяют которые с помощью критериев качества.
4.1 Критериев качества регулирования.
Критериев качества регулирования разделяют на 4 группы:
1. Критерии точности – используют величину ошибки в различных типовых режимах.
2. Критерии величины запаса устойчивости – оценивают удаленность САР от границы устойчивости.
3. Критерии быстродействия – оценивают быстроту реагирования САР на появление задающего и возмущающего воздействий.
4. Интегральные критерии – оценивают обобщенные свойства САР: точность, запас устойчивости, быстродействие.
Существует два основных подхода к оценке качества:
1. Первый использует информацию о временных параметрах системы: h (t), w (t); расположение полюсов и нулей ПФ замкнутой системы Φ(s).
2. Второй использует информацию о некоторых частотных свойствах системы: полоса пропускания; относительная высота резонансного пика; и т.д.
Ошибки системы с астатизмом первого порядка.
Если ПФ САР W (s) обладает астатизмом первого порядка, т.е. в области низких частот W (s)| s →0→ Kv / s. Тогда первая составляющая ошибки:
 ,
,
т.е. в астатической системе первого порядка ошибка от задания равного константе равна нулю, ошибка от задания меняющегося с постоянной скоростью равна xv = v / Kv, а ошибка от задания, меняющегося с постоянным ускорением, нарастает до бесконечности.
Ошибки системы с астатизмом второго порядка.
Если ПФ САР W (s) обладает астатизмом второго порядка, т.е. в области низких частот W (s)| s →0→ K ε/ s 2. Тогда первая составляющая ошибки:
 ,
,
т.е. в астатической системе второго порядка ошибки от заданий равного константе и изменяющегося с постоянной скоростью равны нулю, а ошибка от задания меняющегося с постоянным ускорением равна константе x ε=ε/ K ε.
Коэффициенты ошибок.
Пусть известна ПФ по ошибке Φ x (s), тогда:
X (s)=Φ x (s) G (s)=1/(1+ W (s)) G (s)
где: G (s) – изображение функции g (t).
Разложим Φ x (s) в ряд Тейлора:
X (s)=[ c 0+ c 1 s /1!+ c 2 s 2/2!+ c 3 s 3/3!+…] G (s);
перейдем к оригиналу:
x (t)= c 0 g (t)+ c 1 g ′(t)/1!+ c 2 g ′′(t)/2!+ c 3 g ′′′(t)/3!+…
Величины c 0, c 1, c 2,…, cm – называют коэффициентами ошибок. Их можно определять двумя способами:
1. c 0=Φ x (s)| s →0, cm =[ dm Φ x (s)/ dsm ]| s →0
2. Делением числителя Φ x (s) на знаменатель и сравнением с рядом.
Примечания:
1. Коэффициенты ряда (2) непосредственно связанны с коэффициентом усиления САР, добротностями Kv, K ε,…
| Система \ Ошибки | K & c 0 | Kv & c 1 | K ε & c 2 |
| W (s)=1/ s 0×… | K & 1/(1+ K) | 0 &... | 0 &... |
| W (s)=1/ s 1×… | ∞ & 0 | Kv & 1!/ Kv | 0 &... |
| W (s)=1/ s 2×… | ∞ & 0 | ∞ & 0 | K ε & 2!/ K ε |
2. САР астатическая сигналу задания g (t) может быть статической для f (t), поэтому равенство нулю коэффициентов c 0, c 1, c 2,… для сигнала g (t) не обязательно означает равенство нулю коэффициентов c 0, c 1, c 2,… для сигнала f (t).
3. Ограничение количества членов ряда (2) и предположение о постоянстве коэффициентов ошибок c 0, c 1, c 2,… определяет применение метода для плавно меняющихся сигналов g (t) и f (t), когда переходная составляющая в движении системы успевает затухнуть.
Заключение
Применяя рассмотренные правила преобразования структурных схем, можно любую многоконтурную структурную схему, в том числе и с перекрещивающимися контурами, привести к одноконтурному виду и затем свернуть в одно динамическое звено, передаточная функция которого будет являться передаточной функцией исходной многоконтурной системы.
Список литературы
Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 1987.
В.И. Загинайлов, Л.Н. Шеповалова «Основы автоматики», Москва «КОЛОС», 2001.
Кирюшин О.В. Управление техническими системами: Курс лекций [Электронный ресурс]/ О.В. Кирюшин// Управление техническими системами Учебное пособие.-Уфа: Изд-во УГНТУ, 2003.
Гудинов, В.Н., Корнейчук, А.П. Технические средства автоматизации: Конспект лекций [Текст]/ В.Н. Гудинов, А.П. Корнейчук.
Чекрыжов С.Г Основы теории автоматического управления: Краткий конспект лекций [Электронный ресурс]/ С.Г. Чекрыжов.
Автоматизированное проектирование систем автоматического управления. / Под ред. В.В. Солодовникова. – М.: Машиностроение, 1990.