Теорема. Всякое составное число единственным образом представляется в виде произведения простых сомножителей.

Теорема содержит два утверждения:

1. Разложение на простые множители существует.

2. такое разложение единственно.

Существование. Пусть дано составное число с. Следовательно, у него найдется по крайней мере один простой делитель. Пусть таким делителем будет число р₁ с: р₁ с = р₁с₁, где с₁ – частное.

Если с₁ – простое, то теорема доказана, с > с₁.

Если с₁ – составное, то оно имеет так же хотя бы один простой делитель.

Пусть таким делителем будет число р₂, то есть с₁: р₂ с₁ = р₂с₂ с > c₁ > c₂/

Если с₂ – простое, то теорема доказана и с = р₁ р₂ с₂.

Если с₂ составное, то оно так же имеет хотя бы один простой делитель.

Такой процесс деления не может продолжаться бесконечно, так как чисел, меньших с – конечное множество, следовательно, в конце концов последний множитель окажется простым числом.

Таким образом, будет получено разложение числа с на простые множители, то есть с = р₁ р₂ …р_n.

Единственность данного разложения проведем методом от противного.

Пусть с = р₁ р₂ …р_n с = q₁ q₂ …q_m, где все p_i и q_s – простые множители и n m.

По свойству транзитивности отношения «равно» имеем: р₁ р₂ …р_n = q₁ q₂ …q_m (1)

Левая часть равенства (1) делится на р₁ и, следовательно, правая часть так же делится на р₁. По свойству 5 (произведение простых делится на простое, когда один из сомножителей равен делителю). Пусть р₁ = q₁. сократив равенство (1) на p_i = q_s, получим: р₁ р₂ …р_n–1 = q₁ q₂ …q_m–1. Повторив рассуждения еще раз, получим: р₁ р₂ …р_n–2 = q₁ q₂ …q_m–2.

Если n < m, то после n таких рассуждений придем к равенству: 1 = q₁ q₂ …q_m–n, из которого очевидно, что произведение простых множителей равно 1 тогда, когда каждый из множителей произведения равен 1.

Остается, что n = m. Таким образом, количество сомножителей в данных разложениях совпадает, и все сомножители из разных разложений попарно равны. Что и требовалось доказать.

Определение. Если разложение натурального числа а = , где р₁ <_… < p_n 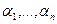– степени соответствующих чисел, то данное разложение называется каноническим разложением натурального числа а.

Например, 840 = 42 × 20 = 2³ × 3 × 5 × 7 840 = 2³ × 3 × 5 × 7 является каноническим разложением числа 840.

Алгоритм Евклида

Чтобы найти наибольший общий делитель чисел а и в, нужно большее число разделить на меньшее; меньшее число разделить на полученный первый остаток; полученный первый остаток разделить на полученный второй остаток и т. д. до тех пор пока не получим деления без остатка; последний делитель, при котором получили деление без остатка есть наибольший общий делитель чисел а и в.

В общем случае процесс нахождения наибольшего общего делителя примет вид:

1. Если а = вq + r НОД (а, в) = НОД (в, r).

2. Если в r НОД (в, r) = r НОД (а, в) = r.

3. Если в = rq₁ + r₁ НОД (r, r₁) = НОД (в, r) = НОД (а, в).

Применяя описанный процесс получим все меньшие и меньшие остатки. В конце концов получим остаток, на который будет делиться на полученный остаток. Этот наименьший, отличный от нуля, остаток и будет наименьшим общим делителем чисел а и в.

Найдем НОД (3075, 60), используя алгоритм Евклида.

3075 60

300 51

75

60

60 15 НОД (3075, 60)

60 4

0

Итак, чтобы найти НОД двух чисел нужно большее число разделить на меньше; меньшее число разделить на полученный первый остаток; полученный первый остаток разделить на полученный второй остаток и т. д. до тех пор, пока не получится деления без остатка. Последний делитель, при котором получилось деление без остатка и есть наибольший общий делитель данных чисел.