Угол с вершиной в центре окружности называется центральным углом.
Градусная мера центрального угла равна градусной мере соответствующей дуги окружности:
∡ AOB= ∪AB.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Вписанный угол измеряется половиной дуги, на которую он опирается:
∡ACB= 
∪AB.
1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
2. Вписанный угол, опирающийся на полуокружность, равен 90°.
Свойство пересекающихся хорд окружности
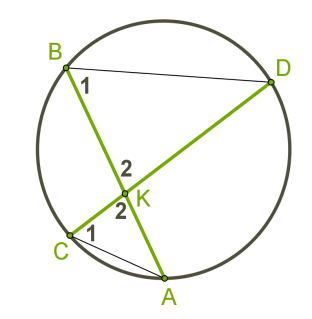
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков второй хорды.
Это свойство легко доказать, дополнив рисунок и рассмотрев подобие ΔCKA∼ΔBKD.
Треугольники подобны, потому что имеют равные углы: ∡1 — вписанные углы, которые опираются на одну и ту же дугу, ∡2 — вертикальные углы.
Если AKKD=CKKB, то AK⋅KB=CK⋅KD.
Задачи
1. Вписанный угол, дана градусная мера дуги
Чему равен вписанный угол, который опирается на дугу,
градусная мера которой равна 115°?
Ответ: вписанный угол равен °.
Шаги решения:
Вписанный угол в два раза меньше дуги, на которую опирается:
∡EDF= ⋅∪EF= ⋅115° = 57,5°.
2. Центральный угол
Чему равен центральный угол, если соответствующий ему вписанный угол равен 137,2°?
Ответ: ∡ FOE = °.
Шаги решения:
Центральный угол в два раза больше соответствующего вписанного угла:
∡ FOE = 2⋅∡EDF= 2⋅137,2° = 274,4°.
3. Градусная мера дуги окружности
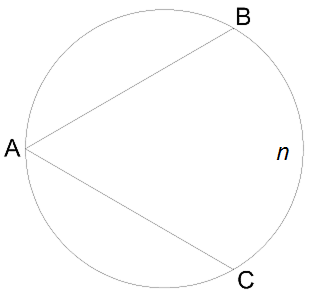
Если угол BAC равен 15°,
то градусная мера дуги BnC равна °.
Шаги решения:
Дуга BnC в два раза больше опирающегося на неё вписанного угла BAC.
|
|
BnC = 2⋅∡BAC;
BnC = 2⋅15°;
BnC = 30°.
4. Вписанный угол
Вычисли угол ASB, если градусная мера дуги ASB равна 258°.
Угол ASB= °.
Шаги решения:
Угол ASB — вписанный, его градусная мера равна половине градусной меры дуги, на которую он опирается.
∢ASB= ∪AkB; ∪AkB=360−258°=102°;∢ASB = 
=51°.
Угол ASB= 51°.
5. Вписанный и центральный угол
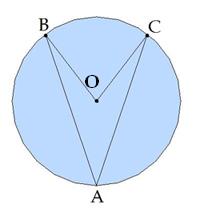
∪AB=107°∪AC=117°
Найти: угол BOC и угол BAC.
Ответ: угол BOC= °, угол BAC= °.
Шаги решения:
Угол BOC опирается на дугу BC, это центральный угол, он равен дуге, на которую опирается.
Угол BOC= ∪ BC=360° − 107° − 117° = 136°;
угол BAC — вписанный угол, который опирается на дугу BC, он равен половине дуги, на которую опирается.
∢BAC= (∪BC); ∢BAC=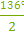 
= 68°
∢BOC=136°, ∢BAC=68°.
6. Хорда окружности
Определи длину хорды CD, если
AM= 2 мм;
MB= 12 мм;
MD = 3 мм.
CM = мм;
CD = мм.
Шаги решения:
1. Чтобы узнать длину хорды CD, надо вычислить длину отрезка CM.
По свойству хорд:
AM⋅MB=CM⋅MD; 2⋅12=3⋅CM;
CM =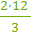 
= 8 мм.
2. CD = CM + MD = 3 + 8 = 11 мм.
Правильный ответ: CD = 11 мм.
7. Центральный угол, углы треугольника
Вычисли углы треугольника AOB, если ∪AnB= 65°, O — центр окружности.
n
∢ ABO= °;
∢ BAO= °;
∢ AOB= °.
Шаги решения:
1. ∢ AOB= ∪ AnB= 65° (т. к. угол AOB — центральный угол, который равен дуге, на которую опирается).
2. Сумма углов треугольника равна 180° и ΔAOB — равнобедренный (т. к. AO=BO как радиусы).
∢ ABO=(180° − 65°):2;
∢ ABO= 57,5° = ∢ BAO.
Правильный ответ: ∢ ABO= 57,5°;
|
|
∢ BAO= 57,5°;
∢ AOB= 65°.
8. Дуги окружности
От точки C на окружности хорда AB видна под углом 57°.
Вычисли градусную меру дуги AB и дуги ACB.
∪AB= °;
∪ACB= °.
Шаги решения:
1. Угол C как вписанный угол равен половине ∪AB:
∪AB=2⋅57°=114°.
2. Так как у обеих дуг общие конечные точки, ∪ACB=360°−∪AB=360°−114°=246°.
9. Угол между хордами
Вычисли угoл ACB, который образуют хорды AC и BC,
если дуга ∪BmC= 17°, дуга ∪AnC= 150°.
Ответ: ∢ ACB= °.
Шаги решения:
Так как хорды имеют общую точку, то обе данные дуги вместе с дугой ∪AB образуют полную окружность с градусной мерой 360°.
Угол ACB между хордами как вписанный угол равен половине дуги, на которую опирается:
∡ACB=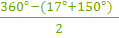 
= 96,5°.
10. Центральный и вписанный в окружность угол
Градусная мера дуги ACB равна 270°.
Найди угол ∡AOB.
Ответ: ∡AOB = °.
Шаги решения:
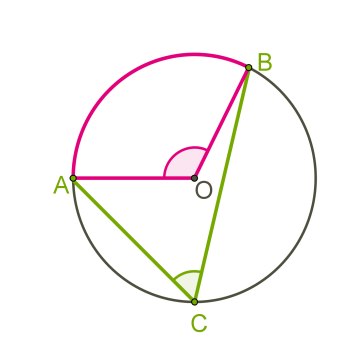
1. ∪AB=360°−270°=90°.
2. Центральный угол равен дуге, на которую опирается.
∡AOB=90°.
11. Отрезки хорды
Две хорды пересекаются. Длина одной хорды равна 5 см, вторая хорда точкой пересечения делится на отрезки 6 см и 1 см. На какие части делится первая хорда?
Введи длину меньшей части (целое число): см.
Введи длину большей части (целое число): см.
Шаги решения:
Дано:
AB и CD — хорды;
M — точка пересечения хорд;
AB= 5 см;
CM= 1 см;
DM= 6 см.
1. Обозначим AM за x. Тогда BM=AB−x= 5 − x.
2. Теорема о пересекающихся хордах: если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков второй хорды.
|
|
AM×MB=CM×MD.
3. Подставляем в данное соотношение обозначенные величины и вычисляем x:
x×(5−x)=1×6;
5x−x2=6;
x2−5x+6=0;
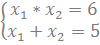
x1=3 см;
x2=2 см.
Так как сумма обоих корней равна 5 см, т. е. длине AB, то можно сделать вывод, что хорда AB делится соответственно на части 3 см и 2 см.
12. Вычисление хорды окружности
Сторона равностороннего треугольника AC длиной 68 см является диаметром окружности. Окружность пересекается с двумя другими сторонами в точках D и E. Определи длину DE.
Ответ: DE= см.
Шаги решения:
1. Проведём DE и радиусы OD и OE.
Треугольники AOD и COE — равнобедренные, так как имеют две равные стороны. Но равнобедренные треугольники с углом 60° (данный треугольник равносторонний) являются равносторонними, то есть все стороны равны и все углы составляют 60°.
2. Следовательно, угол DOE= 60°, что означает, что треугольник DOE — равносторонний.
3. DE= 34 см, так как равен с радиусом окружности (половина диаметра).
13. Отрезки хорды и диаметра
Хорда перпендикулярна диаметру и делит его на отрезки 5 см и 20 см. Определи длину хорды.
Ответ: длина хорды равна см.
Шаги решения:
1. Проведём радиусы OA и OB. Прямоугольные треугольники OAK и OBK равны, у них общий катет OK и равные гипотенузы. Значит, AK=BK.
2. Обозначим AK через x и применим свойство отрезков хорд:
AK⋅BK=CK⋅KD; x2=5⋅20; x= 
; AB= 2x =20 см.
14. Радиус окружности, пропорциональные линии в окружности
Дана окружность (O;OC). Из точки M, которая находится вне окружности, проведена секущая MB и касательная MC.
OD — перпендикуляр, проведённый из центра окружности к секущей MB и равный 5 см.
Найди радиус окружности, если известно, что MB равен 25 см и MC равен 5 см.
Ответ: радиус равен (целое число) см.
Шаги решения:
Дано:
окр. (O;OC);
MB — секущая;
MC — касательная;
OD= 5 см;
MB= 25 см;
MC= 5 см.
1. Квадрат длины отрезка касательной равен произведению секущей, проведённой из той же точки, на её внешнюю часть: MC2=MB⋅MA.
Из этого соотношения выражаем и вычисляем MA:
