Будем считать, что мы поняли, в чем смысл создания расчетных схем, и для дальнейшего решения задач по сопромату необходимо научиться определять реакции опор, иначе приступать к расчету прочности балок нет никакого смысла. Читателям, освоившим эти навыки в курсе теоретической механики (именно освоившим, а не просто сдавшим статику), читать эту главу необязательно. Однако автор настоятельно рекомендует не полениться, и потратить немного времени на изучение этого материала.
Для начала давайте разберемся с самой опорой. Опора – это то, чем балка крепится к чему-либо (или по-другому – это то, на что балка опирается). Вероятнее всего, что само слово пришло в наш обиход из строительства мостов, в более же общем случае это может быть что угодно: деревянная чурка, которую подложили под порог автомобиля при снятии колеса, слесарные тиски, резьбовое соединение и т.д. В теоретической же механике все опоры были классифицированы и разделены на шарнирно-неподвижную, шарнирно-подвижную и глухую заделку. Если теоретическая механика была пройдена и забыта, то знания о данной части статики следует обновить, почитав любой учебник.
Часто студенты «стопорятся» уже на самом понятии реакция, реактивная сила или реактивный момент, поэтому давайте сразу запомним фразу: «Реакция опоры – это СИЛА и (или) МОМЕНТ, которыми опора воздействует на балку». Практически всегда они в начале решения задач для нас неизвестны и их нахождение требует некоторых затрат времени и труда. В то же время решать задачи прочности и жесткости, где есть неизвестные силы невозможно, точнее можно попробовать, только решения не получится.
Рассмотрим уже известную нам двухопорную балку (рисунок 12).

Рисунок 12. Расчетная схема нагружения к рисунку 5.
Здесь F1 и F2 по-прежнему силы, составляющие вес автомобиля на подъемнике. Необходимо определить силы, приходящиеся на опоры балки подъемника, т.е. реакции. Пусть на одно переднее колесо автомобиля приходится F1 =2000Н его веса, на одно заднее F2=3000Н (полная масса автомобиля 1000кг), база автомобиля а=2,5м, b=0,5м,с=0,4м.
Вообще следует разделять понятия массы и веса. Вес – это сила, с которой тело оказывает воздействие на опорную поверхность, и измеряется в Ньютонах, а масса – это мера инертности тела, измеряемая в кг. Эти величины связаны между собой вторым законом Ньютона F=mg, однако в старых учебниках при статических расчетах силы измеряются в кг. В этом нет какой-либо ошибки, и вполне допустимо при условии понимания происходящего, но, возможно, и не очень грамотно в современных условиях.
Вернемся к балке (рисунок 12). Для начала обозначим опоры как “A” и “B”, и их реакции RА и RВ соответственно. Предположим, что реакции направлены вверх. Из курса теоретической механики известно, что для решения подобных задач применяются уравнения статики, а именно: сумма проекций всех сил на каждую из осей и сумма моментов всех сил относительно произвольной точки в плоскости балки. В сопротивлении материалов настоятельно рекомендуется каждую из реакций определять, используя только уравнения моментов. Конечно, можно одну из реакций определить через моменты, а другую через сумму проекций сил, однако этот метод чреват некоторыми опасностями. Так, если при определении первой реакции будет допущена какая-либо ошибка, то она автоматически повторится, при определении второй реакции, поэтому давайте условимся реакции определять только уравнениями суммы моментов, а уравнение суммы сил использовать в качестве проверки.
Итак, составим уравнение суммы моментов относительно опоры А (т.е. учтем все воздействия, которые стремятся повернуть балку вокруг точки А).
ΣМА=0 – в статике все тела находятся в состоянии покоя, т.е. равнодействующая всех сил (и моментов) равна нулю.
Пусть положительное направление будет направлено против хода часовой стрелки
ΣМА=F1b+RВ(a-b-c)-F2(a-b)=0. (1)
Небольшое пояснение. В курсе теоретической механики утверждено правило знаков, где за положительное направление принято вращение против часовой стрелки, за отрицательное - по часовой стрелке. В нашем же случае это не имеет никакого принципиального значения, так как при правильном решении результат будет одинаковым, куда бы мы ни направили положительное направление. А так как мы, решая задачу, работаем ради результата (хотя, есть студенты, которые решают задачи для получения удовольствия J), то положительное направление можно направить куда угодно, предварительно это оговорив.
В результате получилось уравнение (1) с одной неизвестной – непосредственно с реакцией RВ. Решим это уравнение
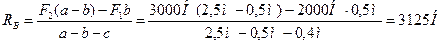 (2)
(2)
Аналогично, составив уравнение суммы моментов относительно точки В, получим реакцию RВ.
ΣМВ=0 (3)
ΣМВ=F1(a-c)-Ra(a-b-c)-F2c=0 (4)
 (5)
(5)
Здесь в обоих случаях значения реакций получились положительными, следовательно, предположения о направлении реакций оказались верными (отрицательные значения реакций говорят о противоположном направлении реакций). Однако следует убедиться в правильности полученных значений, иначе при дальнейшем расчете на прочность балки, обнаружится ошибка, и задачу придется решать заново. Для проверки рекомендуется использовать уравнение суммы сил, действующих на балку, а именно: сумма внешних сил должна быть равна сумме реакций (так как балка находится в покое).
В рассматриваемом случае сумма сил F1+F2=5000Н (половина веса автомобиля), сумма реакций также равна 5000Н, т.е. все внешние силы распределились по опорам. Для проверки реакций можно также составить уравнение суммы моментов относительно любой другой точки балки (не только опор), и она должна быть равна нулю.
Построение эпюр.
Для начала немного о терминах и определениях. Эпюрой называется диаграмма изменения внутренних силовых факторов (ВСФ или просто внутренних сил) по длине балки. Как правило, требуется построить эпюры поперечных (перерезывающих) сил и изгибающих моментов. Не будем останавливаться на их определениях, а приступим к примеру (рисунок 13).
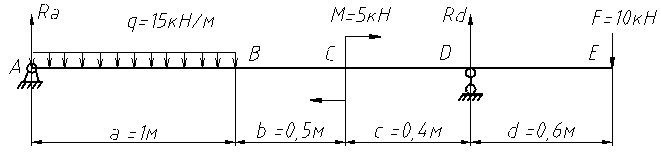
Рисунок 13. Схема нагружения балки.
На данном рисунке изображена некоторая балка, нагруженная распределенной нагрузкой, сосредоточенной силой и сосредоточенным моментом. В общем случае, уравнения, описывающие изменение поперечных сил Q и изгибающих моментов М в зависимости от координат точек балки (Z) на разных участках будут иметь разный вид. Поэтому необходимо разбить балку на участки. Не вдаваясь в теоретические обоснования, можно предложить «чисто техническое» решение этого вопроса: провести вертикальные отрезки через крайние (левую и правую) точки, через точки, в которых находятся опоры, где приложены сосредоточенные силы и моменты, а так же точки, ограничивающие зону действия распределенной нагрузки. Для удобства балка уже разбита на участки, и обозначены реакции опор. Определим значения реакций опор. Составляем уравнение моментов относительно (вокруг) точки А. За положительное направление принимаем «по ходу часовой стрелки».
 ; (6)
; (6)
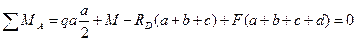 (7)
(7)
В первом слагаемом данного уравнения учтено действие распределенной нагрузки, а именно: распределенная нагрузка заменена сосредоточенной силой (Qa), приложенной посередине участка. Подробно останавливаться на этом не будем. Определим из данного уравнения неизвестную реакцию.
 (8).
(8).
После подстановки числовых значений получим RD=19,7кН.
Найдем реакцию RA, составив уравнение суммы моментов относительно точки D.
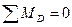 (9)
(9)
 (10)
(10)
 (11)
(11)
Сумма сил, действующих на балку, составляет 25кН, сумма реакций также 25кН, следовательно, реакции определены правильно.
Приступаем, непосредственно, к решению задачи на прочность. Нам необходимо построить эпюры поперечных сил и изгибающих моментов, используя метод сечений.
Итак, рассекаем первый участок балки на некотором расстоянии Z1 от левого конца и рассматриваем только часть балки до места рассечения (рисунок 14). Эта часть балки находится в равновесии, так как вся балка тоже была уравновешена, однако на неё действуют не все внешние нагрузки, следовательно, её уравновешивает внутренняя поперечная сила Q. (Обратите внимание, что на рисунке 14 не изображена опора, так как она была заменена её реакцией). Следовательно, поперечная сила Q равна сумме всех сил, действующих на рассматриваемую часть балки.

Рисунок 14. Отсеченный первый участок
Очень часто студентам тяжело это освоить, так как интуиция (жизненный опыт) многих людей сталкивает на изгиб балки (согласитесь, по рисунку 14 «явно видно, что балку куда-то должно гнуть»). Изгиб этого же участка мы рассмотрим позже, а сейчас чтобы понять происходящие явления, прошу всех посмотреть на рисунок 15. На данном этапе решения задачи мы рассматриваем только равновесие сил, куда бы они ни были приложены, как не имеет значения, на какое место чаши весов кладутся гири и то, что взвешивают.
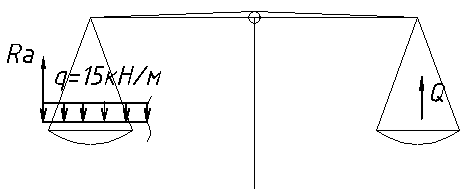
Рисунок 15. Пояснение к определению поперечной силы
Очень часто в учебниках уравнения равновесия участка балки начинают с суммы всех сил, равной нулю, при этом обязательно вспоминая правило знаков. В учебниках, конечно, все написано правильно, однако сейчас давайте без лишних фраз закончим работу с рисунком 14. Согласно этого рисунка поперечная сила будет равна
 (12).
(12).
Следовательно, зная, что координата Z1 в данной ситуации может меняться 0≤Z1≤1м (длина первого участка балки на рисунке 13 составляет 1м), мы можем определить значение поперечной силы в любой точке первого участка балки. Как правило, требуется знать значения внутренних сил в ключевых точках (на концах участка), при условии, что уравнение линейное.
Найдем значение поперечной силы в начале участка, подставив Z1=0 (т.е. силу в точке А), тогда
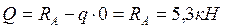 (13).
(13).
Найдем значение силы на конце первого участка (в точке В, Z1=1м)
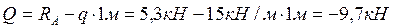 (14).
(14).
Как видим, поперечная сила в какой-то точке участка поменяла знак, т.е. в которой график сил перейдет через ноль. Найдем координату этой точки, так как она будет иметь важное значение при определении изгибающего момента.
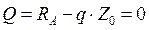 (15);
(15);
Z0=0,35м.
О правиле знаков, которое гласит: «Если рассматриваемый (отсеченный) участок балки под действием сил стремится повернуться по ходу часовой стрелки, то тогда поперечная сила принимает положительное значение, если против часовой стрелки – то отрицательное». Довольно громоздкое правило, если учесть что не всегда удается сразу предположить направление поперечной силы. Поэтому то же самое можно огласить другими словами: «При составлении уравнения поперечных сил Q=f(Z), при рассмотрении балки слева направо, все силы направленные вверх подставляем со знаком «+», силы, направленные вниз, будут иметь отрицательное значение. При рассмотрении справа налево знаки меняются на противоположные». Пользоваться можно любым из этих правил, кому какое больше нравится (или меньше не нравится J).
Рассмотрим второй участок, рисунок 16, 0≤Z2≤0,5м

Рисунок 16. Определение поперечной силы на втором участке
Записываем уравнения равновесия для этого участка
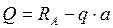 (16).
(16).
Как видно в уравнение равновесия этого участка координата Z2 не входит, следовательно, значение поперечной силы не зависит от места рассечения и на данном участке будет постоянным
 (17).
(17).
Далее будем рассматривать балку с другого конца для упрощения последующих расчетов. Рассечем четвертый участок DE (0≤Z4≤0,6м), рисунок 17. Составим уравнение равновесия этого участка, не забывая о том, что идем справа налево
Q=F=Q=10кН (18).

Рисунок 17. Определение поперечной силы на последнем участке
Как можем видеть, уравнение очень простое, и в него не входит координата Z4, следовательно на всем протяжении участка значение поперечной силы также изменяться не будет.
Рассмотрим третий участок, рисунок 18, (0≤Z3≤0,4м).

Рисунок 18. Определение поперечной силы на третьем участке
По образу и подобию с другими участками определяем значение поперечной силы Q=F-Rd=10кН-19,7кН=-9,7кН. На этом участке значение силы также не зависит от текущей координаты.
На этом определение поперечных сил можно считать завершенным, осталось лишь по найденным значениям построить соответствующую эпюру, рисунок 19.

Рисунок 19. Эпюра поперечной силы.
Рассмотрим изгибающие моменты, действующие в балке. Для этого также рассекаем балку на каждом из участков и пишем уравнения моментов. Рассечем первый участок, рисунок 20. Здесь мы рассматриваем все воздействия, которые балку изгибают, причем рассматриваем все то, что её изгибает относительно (вокруг) точки рассечения.

Рисунок 20. Определение момента на первом участке
Рассмотрим первый участок. Сумма моментов относительно точки рассечения
 (19).
(19).
Внимательно присмотримся к этому уравнению. Начнем с правила знаков, которое гласит: «Рисуй момент со стороны сжатых волокон». На первый взгляд (а кому-то и на второй и на третий) в этой фразе нет никакого смысла. Однако если немного включить фантазию, то выяснится, что при изгибе балки всегда с одной стороны происходит растяжение материала, а с противоположной стороны сжатие. В нашем случае реакция RA стремится согнуть балку вверх, следовательно, сжатые волокна находятся сверху, и соответствующий момент (RAZ1) имеет положительное значение. Распределенная нагрузка сгибает балку вниз, соответственно сжатые волокна от этой нагрузки снизу, и соответствующее слагаемое
( ) (20)
) (20)
имеет отрицательное значение. Повторюсь, что при работе с распределенной нагрузкой необходимо мысленно заменить ее сосредоточенной силой, приложенной к середине участка. Следствием из соответствующих преобразований является вторая степень переменной.
Найдем значения изгибающего момента в начале и конце участка. Момент в точке А, координата Z1=0
 (21).
(21).
Момент в точке В, координата Z1=а=1м
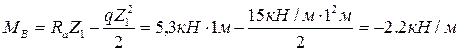 (22).
(22).
Вспомним, что когда строили эпюру поперечных сил, то выяснили, что где-то на первом участке сила переходит через ноль, и мы определили соответствующую координату (тогда мы её обозвали Zx). Определим значение момента в этой точке
 (23).
(23).
Как можно заметить в этой точке значение изгибающего момента больше, чем по краям участка, забегая вперед, скажем, что оно максимальное на этом участке, а может быть и на всей балке.
Так же следует знать, что уравнение моментов на данном участке из-за наличия распределенной нагрузки получилось второй степени, следовательно точки эпюры следует соединять параболой.
Рассмотрим второй участок, рисунок 21. Составим уравнения моментов относительно точки рассечения
 (24).
(24).

Рисунок 21.Определение момента на втором участке
Здесь мы по-прежнему заменяем распределенную нагрузку сосредоточенной, приложенной посередине участка. Найдем значение изгибающего момента по краям участка. В точке B значение момента мы уже нашли при работе с предыдущим участком, и оно равно М=-2,2кН/м. Если кто не верит, то можете подставить в уравнение моментов этого участка Z2=0, и получится уравнение моментов предыдущего участка для правого конца.
Найдем значение изгибающего момента в точке C (Z2=0,5м).
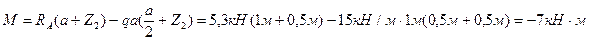 (25).
(25).

Рисунок 22. Определение момента на последнем участке
Далее для упрощения вычислений будем рассматривать балку с другого конца. Рассмотрим четвертый участок, рисунок 22. Составляем уравнение изгибающего момента
 (26).
(26).
Отрицательное значение момента на данном участке обусловлено тем, что сжатые волокна балки здесь находятся снизу. Найдем значения моментов по краям участка. Момент в точке Е будет равен нулю, так как значение переменной здесь Z4=0.
Определим момент в точке D
 (27).
(27).
Все что нам осталось, определить моменты на третьем участке, рисунок 23. Значение момента в точке D нам определять уже не нужно, так как мы его уже определили на предыдущем участке. Кто-то наверняка скажет, что и значение момента в точке C мы тоже определили, когда работали со вторым участком, однако давайте не поленимся и найдем его
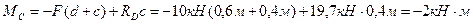 (28)
(28)

Рисунок 23. Определение момента на третьем участке
Почему полученное значение в данной точке не получилось равным значению момента в этой же точке, но на втором участке? Давайте посмотрим, на какую величину различаются значения моментов, а различаются они на 5кН*м. Именно такую величину составляет сосредоточенный момент, приложенный в точке C, и он вызывает такое резкое изменение эпюры. В завершение осталось расставить все полученные точки на эпюре, соединить их линиями, чтобы получилось как на рисунке 24.
Основной целью этих задач является определение максимального значения абсолютной величины изгибающего момента и точки её расположения, так как балки разрушаются от действия максимально момента (ломает не сила, ломает момент). В нашем случае опасной точкой является точка С, потому что на нее приходится максимальное значение момента по модулю – 7кН*м. При дальнейших расчетах на прочность знаки, как правило не учитываются, так как когда балка разрушается, то уже не имеет значения в какую сторону (так же придавленному человеку абсолютно неинтересно в плюс или минус сломалась балка, под которой он лежит L).

Рисунок 24.
Однако возникает вопрос: «Зачем строили эпюру сил»? Её мы строили для быстрой проверки правильности построения эпюры моментов. Дело в том, что функция сил является производной от функции моментов, и все свойства производной, изученные в курсе математики, здесь работают. Следствием из этого являются следующие правила построения эпюр (в подтверждение можно также смотреть на рисунки 24 и 25):
1) На тех участках, где нет распределенной нагрузки, эпюра Q ограничена прямыми, параллельными оси эпюры, а эпюра М, в общем случае, – наклонными прямыми.
2) На тех участках, где к балке приложена равномерно распределенная нагрузка, эпюра Q ограничена наклонными прямыми, а эпюра М – квадратичными параболами. При построении эпюры М на сжатых волокнах, выпуклость параболы обращена в сторону, противоположную действию распределенной нагрузки
3) В тех сечениях, где Q = 0, касательная к эпюре М параллельна оси эпюры. Изгибающий момент в таких сечениях балки экстремален по величине (Мmax, Mmin).
4) На участках, где Q > 0, M возрастает, то есть слева на право положительные ординаты эпюры M увеличиваются, отрицательные – уменьшаются; на тех участках, где Q < 0, M убывает
5) В тех сечениях, где к балке приложены сосредоточенные силы:
а) на эпюре Q будут скачки на величину и в направлении приложенных сил.
б) на эпюре M будут переломы, острие перелома направлено против действия силы.
6) В тех, сечениях, где к балке приложены сосредоточенные моменты, на эпюре M будут скачки на величину этих моментов, на эпюре Q никаких изменений не будет
7) Если на конце консоли или в концевой опоре приложен сосредоточенный
момент, то в этом сечении изгибающий момент равен внешнему моменту
8) Эпюра Q представляет собой диаграмму производной от эпюры M. Значит, ординаты Q пропорциональны тангенсу угла наклона касательной к эпюре M


Рисунок 25. Пояснение к свойствам эпюр.
В заключение стоит добавить следующее. Не смотря на подробное развитие теоретического аппарата для данной темы, без практики невозможно научиться решать такие задачи. Это сродни тому, как невозможно научиться играть на скрипке, только наблюдая как играют другие.
Вопросы для самопроверки
1. На рисунке 26 показан кран-балка. При одинаковом по весу грузе наиболее тяжелый случай нагружения будет в случае когда таль находится в середине балки, либо на краю?

2. Как будет меняться схема нагружения моста, показанного на рисунке 27, в зависимости от количества находящихся на нем кораблей?

Рисунок 27.
3. Как связаны между собой поперечная сила и изгибающий момент в любой точке (сечении балки)?
4. Какое значение принимает изгибающий момент в точке (сечении балки), где поперечная сила меняет знак?
5. Какие изменения происходят на эпюрах поперечных сил в точках (сечениях), где к балке приложены сосредоточенные силы?
6. Какие изменения происходят на эпюрах поперечных сил в точках (сечениях), где к балке приложены сосредоточенные моменты?
7. Как выглядят эпюры поперечных сил и изгибающих моментов на участках где к балке приложена распределенная нагрузка?
8. Как выглядят эпюры поперечных сил и изгибающих моментов на участках, где не действует распределенная нагрузка?
Список литературы
1. Кочетов В.Т. Сопротивление материалов/ В.Т.Кочетов, А.Д. Павленко, М.В. Кочетов. – Ростов –на –Дону: Феникс, 2001.- 368с.
2. Пособие к решению задач по сопротивлению материалов: Учеб. пособие для техн. вузов / Миролюбов И.Н., Енгалычев С.А., Сергиевский Н.Д. и др. – 5-е изд., перераб. И доп. – М.: Высш. шк., 1985. – 399с.
3. Ицкович Г.М. Сопротивление материалов: Учеб. для учащихся машиностроит. техникумов. – 7-е изд., испр. – М.: Высш. шк., 1986. – 352с.: ил.
Индивидуальное задание
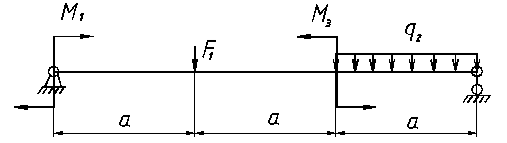
В процессе обучения сопротивлению материалов студенту необходимо выполнить индивидуальное домашнее задание. Вариант задания представляет собой два числа, сообщаемые преподавателем каждому из студентов. Первая цифра – это номер варианта схем, представленных на страницах 30-39. Вторая цифра – номер варианта данных согласно таблице 1. Индивидуальное задание выполняется рукописно на листах бумаги, формата А4.
Таблица 1
Данные для решения задач
| № | а, м | q1=q3, кН/м | q2, кН/м | F1, кН | F2, кН | F3, кН | М1, кН∙м | М2, кН∙м | М3, кН∙м |
| 0,8 | |||||||||
| 1,2 | |||||||||
| 1,4 | |||||||||
| 1,6 | |||||||||
| 1,8 | |||||||||
| 0,8 | |||||||||
| 1,2 | |||||||||
| 1,4 | |||||||||
| 1,6 | |||||||||
| 1,8 | |||||||||
| 0,8 | |||||||||
| 1,2 | |||||||||
| 1,4 | |||||||||
| 1,6 | |||||||||
| 1,8 |
ВАРИАНТ 1
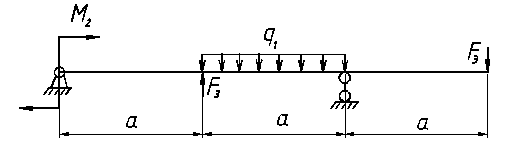




ВАРИАНТ 2
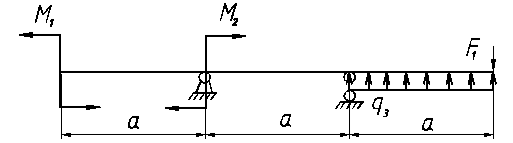

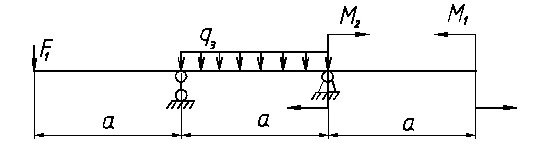
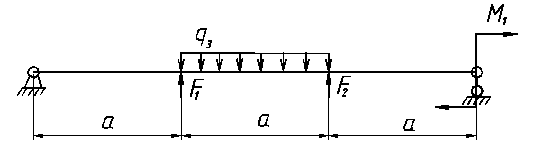


ВАРИАНТ 3
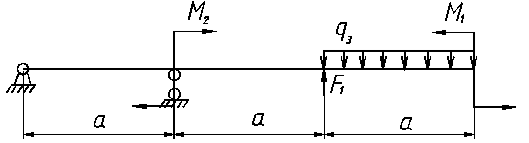



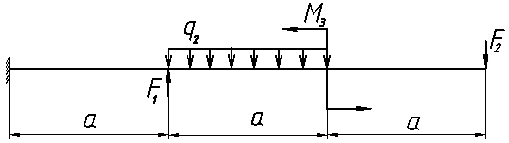

ВАРИАНТ 4
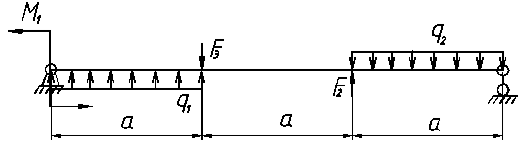




ВАРИАНТ 5





ВАРИАНТ 6



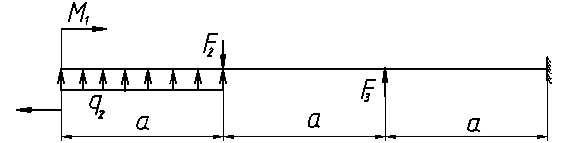
ВАРИАНТ 7

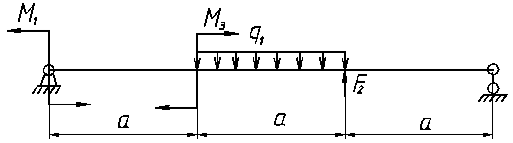




ВАРИАНТ 8
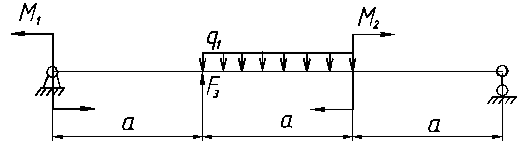



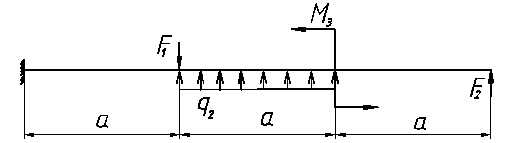

ВАРИАНТ 9




ВАРИАНТ 10




Содержание
Предисловие…………………………………………...…………………………3
С чего начинается сопромат…………………………………………………….4
Определение реакций опор………………………..…………………………...10
Построение эпюр……………………………………………………………….13
Вопросы для самопроверки……………………………………………………26
Список литературы……………………………………………………………..28
Индивидуальное задание………………………………………………………29