Примеры решения расчетных задач

Ход занятия

Для выполнения задания необходимо вспомнить основные характеристики волны и записать в тетради: амплитуда волны, фаза волны. Также следует вывести уравнение стоячей волны, чтобы убедиться в том, что стоячая волна образуется в результате интерференции бегущей и отраженной волны.

Качественные задачи

1. 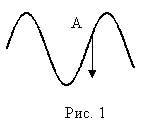В бегущей волне частица А имеет направление скорости, указанное на рис. 1. В каком направлении "движется" волна?

2. Почему не могут быть поперечными упругие волны в газе?

3. При образовании волн частицы воды не перемещаются вдоль направления их распространения, а лишь участвуют в колебательном движении около некоторого среднего положения. Почему же морское волнение часто выбрасывает на берег различные плавающие в море предметы?

4. Может ли существовать в природе плоская гармоническая волна, или это физическая идеализация, лишь приближенно описывающая реальность?

5. Могут ли космонавты при выходе в открытый космос общаться между собой при помощи звуковой речи?

6. В воду погружен вибратор, мембрана которого издает музыкальные звуки. Будет ли находящийся под водой пловец воспринимать мелодию такой же, какой он слышал бы ее в воздухе?

7. Перед игрой инструменты "настраивают". В чем физическая сущность настройки скрипки, мандолины и других струнных инструментов?

Примеры решения расчетных задач

Задача 1. Плоская волна с периодом Т = 1,2 с и амплитудой колебаний a = 2 см распространяется со скоростью v = 15 м/с. Чему равно смещение ξ(x,t) точки, находящейся на расстоянии х = 45 м от источника волн, в тот момент, когда от начала колебаний источника прошло время t = 4 с?

Решение:

Воспользуемся уравнением плоской волны

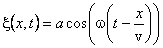. (1)
Частота связана с периодом колебаний соотношением 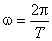. Подставим значение частоты в уравнение (1).

.
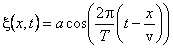Подставляя в последнее выражение численные значения величин, получи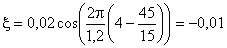м

м.

Ответ: ξ = -0,01 м.

Задача 2. Две точки находятся на расстоянии Δ x = 50 см друг от друга на прямой, вдоль которой распространяется плоская волна со скоростью v = 50 м/с. Период колебаний Т равен 0,05 с. Найдите разность фаз Δφ колебаний в этих точках.

Решение:

Фаза плоской волны равна . Разность фаз в двух точках пространства, охваченного волновым процессом, в момент времени t определяется соотношением

.
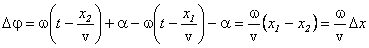Подставляя численные значения и учитывая, что 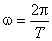, получим

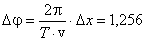рад.

Ответ: Δφ = 1,256 рад.

Задача 3. Звуковые колебания, имеющие частоту ν = 0,5 КГц и амплитуду a, равную 0,25 мм, распространяются в упругой среде. Длина волны λ = 70 см. Найдите:

1. скорость распространения волн;

2. максимальную скорость частиц среды.

Решение:

Скорость распространения волны связана с длиной волны соотношением

λ = v· T, (2)
где Т - период колебаний частиц среды. Период колебаний связан с частотой колебаний ν соотношением

. (3)
Из (2) и (3) получим для скорости распространения волны

v = λ·ν = 350 м/с.
Для ответа на второй вопрос воспользуемся уравнением плоской волны

.
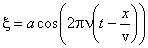Чтобы найти скорость частиц среды, нужно взять производную от смещения по времени

.
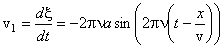Отсюда видно, что максимальная скорость движения частиц среды будет равна

v_1max = 2 π v a = 0,79 м/с.

Ответ: 1) v = 350 м/с; 2)v_1max = 2 π v a = 0,7 м/с.

Задача 4. Две волны ξ ₁ = a sin(ω t-kx) и ξ ₂ = a sin(ω t+kx) с одинаковыми частотами ν = 4 Гц распространяются со скоростью v = 960 см/с. Они интерферируют между собой и образуют стоячую волну. Определите амплитуду точек стоячей волны через каждые l = 20 см, начиная отсчет от узла. Определите величину смещения и скорость этих точек в момент времени 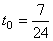с.

Решение:

Стоячая волна возникает в результате интерференции при сложении ξ₁ и ξ₂.

ξ = ξ₁+ξ₂ = 2 a cos(kx)sin(2πν t).
Из уравнения стоячей волны видно, что в каждой точке пространства происходят колебания с частотой ω. При этом амплитуда колебаний в точке х равна

A = 2 a |cos kx |.
Следовательно, в точках, в которых cos kx = 0, колебания отсутствуют. Эти точки являются узлами стоячей волны. Координата первого узла определяется из соотношения 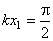. Учитывая, что 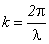, получим 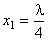. Расстояние между двумя соседними узлами равно см.

Следовательно, между двумя узлами будет находиться n = 5 точек, удовлетворяющих условию задачи. Координаты этих точек будут равны

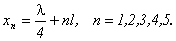
Амплитуда колебаний в этих точках определяется из условия:

.
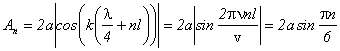Подставляя значения n, получим A ₁ = a, A ₂ = 1,73 a, A ₃ = 2 a, A ₄ = 1,73 a, A ₅ = a.

Смещение найденных точек от положения равновесия можно найти из уравнения стоячей волны.

.
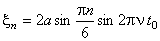Подставляя численные значения, получим ξ₁ = 0,866 a, ξ₂ = 1,5 a, ξ₃ = 1,732 a, ξ₄ = 1,5 a, ξ₅ = 0,866 a.
Чтобы найти скорость этих точек, нужно взять производную от смещения ξ по времени

.
Подставляя численные значения, получим: V ₁ = 1,566 a, V ₂ = 2,174 a, V ₃ = 3,132 a, V ₄ = 2,174 a, V ₅ = 1,566 a.

Ответ: A ₁ = a, A ₂ = 1,73 a, A ₃ = 2 a, A ₄ = 1,73 a, A ₅ = a;
ξ₁ = 0,866 a, ξ₂ = 1,5 a, ξ₃ = 1,732 a, ξ₄ = 1,5 a, ξ₅ = 0,866 a;
V ₁ = 1,566 a, V ₂ = 2,174 a, V ₃ = 3,132 a, V ₄ = 2,174 a, V ₅ = 1,566 a.

Задача 5. В упругой однородной среде распространяются две плоские волны - одна вдоль оси Х, другая вдоль оси Y: ξ ₁ = a cos(ω t-kx), ξ ₂ = a cos(ω t-ky). Найдите характер движения частиц среды в плоскости XY, если обе волны поперечные и направление колебаний одинаково.

Решение:

Воспользуемся принципом суперпозиции волн, тогда результирующий волновой процесс будет описываться уравнением:

.
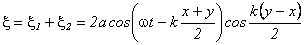Из полученного уравнения видно, что в точках, для которых выполняется условие 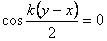, колебания отсутствуют. Координаты этих точек будут удовлетворять условию 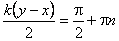, где n = 0, 1, 2, …
Учитывая, что волновое число 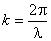, получим, что частицы среды не совершают колебания вдоль прямых, уравнения которых имеет вид

.
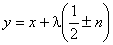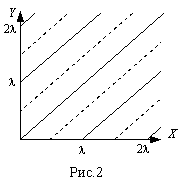
На рис. 2 эти прямые проведены пунктиром.

Если , частицы среды колеблются с максимальным отклонением. Этому условию удовлетворяют точки, координаты которых можно получить из условия 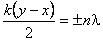, где n = 0, 1, 2, … После подстановки значения 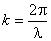получим уравнение прямых y = x ± n λ. На рис. 2 эти прямые проведены сплошными линиями.