Пример 1. Заданы координаты вершин А (1.1), В(2.7), С(3,5) треугольника АВС.
Требуется:
1). Построить треугольник в системе координат Оху.
2). Вычислить его периметр.
3). Найти уравнения сторон треугольника (с проверкой).
Решение.
1) Строим треугольник по координатам его вершин.
2) Периметр треугольника – это сумма длин его сторон. Длина стороны – это расстояние между двумя точками плоскости:
АВ = 
 =
= 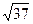

ВС= 
АС= 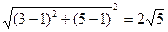
Р= АВ+ВС+АС= 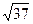 +
+  +2
+2  =
= 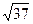 +3
+3 
3) Уравнение сторон – это уравнение прямых, проходящих через две точки:
уравнение прямой АВ:
 =
=  , 6x-y-5=0
, 6x-y-5=0
Проверка: подставим в подчеркнутое уравнение координаты точек А и В
2 2+7-11=0 (верно) 2 3+5-11=0 (верно)
Уравнения остальных сторон треугольника получим аналогично.
Пример 2. Найти точку пересечения прямых и построить прямые
х-3у+2=0 и3х+у-3=0 
Решение. Для нахождения точки пересечения непараллельных прямых следует решить систему двух уравнений с двумя неизвестными х и у
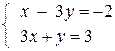
Для этого можно использовать формулы Крамера
х =  , у =
, у =  , где
, где
 0 - главный определитель системы (определитель коэффициентов при неизвестных),
0 - главный определитель системы (определитель коэффициентов при неизвестных), 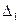 - определитель х, полученный из главного определителя системы заменой первого столбца столбцом правых частей системы,
- определитель х, полученный из главного определителя системы заменой первого столбца столбцом правых частей системы,
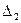 - определитель у, полученный из главного определителя системы заменой второго столбца столбцом правых частей системы
- определитель у, полученный из главного определителя системы заменой второго столбца столбцом правых частей системы
 =1+9=10
=1+9=10 

х =0,7 у=0,9
Подставляя найденные значения х и у в оба уравнения прямых, убеждаемся, что каждое уравнение обращается в тождество
0,7-3 0,9=-2 (верно) 3 0,7+0,9=3 (верно).
Таким образом, х =0,7 у=0,9 - координаты точки пересечения прямых.
Далее следует построить прямые и сравнить графическое решение с полученным результатом. Отметим, что данные прямые взаимно перпендикулярны.
Пример 3. Решить систему линейных уравнений с проверкой методом Крамера. 
Решение. Формулы Крамера имеют вид:
х  =
=  , х
, х  =
=  , х
, х  =
=  , где
, где
 0 - главный определитель системы (определитель матрицы коэффициентов при неизвестных),
0 - главный определитель системы (определитель матрицы коэффициентов при неизвестных),  (i=1,2,3) – определитель, полученный из главного, заменой i столбца столбцом свободных членов.
(i=1,2,3) – определитель, полученный из главного, заменой i столбца столбцом свободных членов.
Для вычисления определителя третьего порядка, используем разложение определителя по элементам первой строки
 1
1  - 2
- 2  + 3
+ 3  =(-6-1)-2 (-4-3)+3(2-9) =-7+14-21=-14
=(-6-1)-2 (-4-3)+3(2-9) =-7+14-21=-14
 =
=  =-14,
=-14, 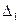 =
=  =-28,
=-28, 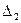 =
=  =0,
=0, 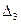 =
=  =14
=14
х  =2, х
=2, х  =0, х
=0, х  =-1.
=-1.
Проверка: подставляем полученные значения переменных в левую часть исходной системы:
2-3=-1 (верно), 4-1=3 (верно), 6+2=8 (верно).
Ответ: х  =2, х
=2, х  =0, х
=0, х  =-1
=-1
4. Решить однородную систему (с проверкой); предварительно вычислить главный определитель системы.

Метод Крамера не является универсальным, поскольку предполагает, что главный определитель системы отличен от нуля.
Универсальным методом решения систем является метод Гаусса
(метод исключения неизвестных). Покажем его реализацию на примере решения однородной системы, главный определитель которой равен нулю. Действительно  =
=  =0
=0
Для реализации метода Гаусса расширенную матрицу системы приводят к ступенчатому виду
А 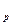 =
= 

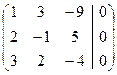




 Последняя матрица соответствует системе, равносильной исходной
Последняя матрица соответствует системе, равносильной исходной
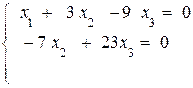
откуда видно, что система имеет бесчисленное множество решений,так как неизвестных три, а уравнений два.
х  полагаем равным произвольному числу t (свободное неизвестное): х
полагаем равным произвольному числу t (свободное неизвестное): х  =t, тогда х
=t, тогда х  =23t/7, х
=23t/7, х  =-6t/7.
=-6t/7.
Проверка: подставляем полученные значения переменных в левую часть исходной системы:
-18t/7+46t/7-4t=0 (верно)
-12t/7-23t/7+5t=0 (верно)
-6t/7+69t/7-9t=0 (верно)
Ответ: х  =-6t/7, х
=-6t/7, х  =23t/7, х
=23t/7, х  =t (t- произвольное число).
=t (t- произвольное число).
Заметим, что однородная система всегда имеет нулевое решение. Если главный определитель однородной системы равен нулю, то она имеет бесчисленное множество решений, то есть решения отличные от нулевого.