Пример 1. Задан ряд распределения случайной величины
Вероятности рi заданы произвольно, исходя из условия: сумма их равна 1
------------------------------------------
хi 1 2 3 4 5 6
------------------------------------------
рi 0,1 0,3 0,2 0,1 0,2 0,1
Требуется:
1). Найти математическое ожидание и дисперсию.
2) Найти вероятности следующих событий: случайная величина примет значение
а) не больше единицы;
б) не меньше своего математического ожидания.
Решение. 1) Здесь используются формулы для математического ожидания
М(X)= х 
р +х 
р +…+х 
р
и дисперсии
D(X)=(х ) 
р +(х ) р +…+(х ) р -(М(X))
Подставляя в формулы значения из таблицы, вычислим
М(X)= 1 0,1+2 0,3+3 0,2+4 0,1+5 0,2+6 0,1= 3,3
D(X)=1 0,1+4 0,3+9 0,2+16 0,1+25 0,2+36 0,1-(3,3) = 2,41
2) а) Р(X 
1)= 0,1; б) Р(X 
3,3)=0,1+0,2+0,1= 0,4
Пример 2. Стрелок делает по мишени n независимых выстрелов. Вероятность попадания при каждом выстреле одинакова и равна р.
Требуется:
1)Построить ряд распределения числа попаданий.
2)Найти математическое ожидание и дисперсию числа попаданий.
3)Найти вероятность хотя бы одного попадания.
Решение. Пусть n=3; p=0,3. При решении задачи следует использовать формулу биномиальное распределения:
P (k)=C 
p 
(1-p) 
, k=0;1;;n
1)Ряд распределения числа попаданий имеет вид таблицы
k 0 1 2 3
-------------------------------------------------
р 0,343 0,441 0,189 0,027
Проверка. 0,343 + 0,441 + 0,189 + 0,027 =1
2) Математическое ожидания и дисперсию числа попаданий можно найти по формулам для биномиального распределения: М(X)=n p; D(X)=n p(1-p)
М(X)=3 0,3= 0,9; D(X)=3 0,3 0,7= 0,63. 3) P (X 1)=1- P (X=0)=1-0,343= 0,657
Пример3. В урне имеются а белых и b черных шаров. Вынимают 2 шара.
Требуется:
1) Построить ряд распределения числа черных шаров среди вынутых.
2) Найти математическое ожидание и дисперсию числа черных шаров.
Решение. Пусть а=3 b=4.
1) Очевидно, что случайное число Х 
черных шаров может принимать значения
0; 1; 2. Найдем вероятности этих значений. Обозначим событие А- вынутый
шар белый, событие В – вынутый шар черный. Индекс 1 означает 1-ый вынутый шар, индекс 2 означает 2-ой вынутый шар.
Р(X=0)=Р(А А 2)= 
= 
,
Р(X=1)=Р(А В + В А )= 
++ 
= 
,
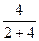Р(X=2)=Р(В1В )= 
= 
.
Ряд распределения числа черных шаров имеет вид 
2). М(X)= 
. D(X)= 
- 
= 
Пример 4. Стрелок ведет независимую стрельбу до первого попадания, имея в запасе n патронов. Вероятность попадания при одном выстреле равна р.
Требуется:
1) Построить ряд распределения числа израсходованных патронов.
2) Найти математическое ожидание числа израсходованных патронов.
(n,p из примера 2)
Решение. n=3, p=0,3. 1). Очевидно, что случайное число израсходованных патронов может принимать значение 1, 2, 3. Найдем вероятности этих значений.
Обозначим события А 
- попадание при i выстреле, 
- промах при i выстреле. События А и независимы.(i=1,2,3).
Р(X=1)=Р(А )=0.3. Р(X=2)=Р( А )=0,7 0,3=0,21. Р(X=3)=Р( )=(0,7) =0,49.
Таким образом, ряд распределения имеет вид
М(X)=1 0,3+2 0,21+3 0,49= 2,19. D(X)=1 0,3+4 0,21+9 0,49-(2,19) = 0,754
5. Дана выборка
| xi |
Требуется:
1) Построить вариационный ряд.
2) Вычислить выборочные среднее, дисперсию, среднеквадратичное отклонение.
Решение
Здесь дана выборка объема n=10.
1). Вариационный ряд- это зависимость абсолютной частоты варианта ni от значения варианта xi. Эту зависимость можно представить в виде таблицы
| xi | |||||
| ni |
2) Выборочное среднее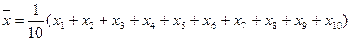 
= 3,1
выборочная дисперсия и среднеквадратичное отклонение
Dв =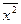 
-( 
) =12,3- 9,61= 2,69, 
= 1,64,
где
= 
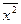=12,3
6. Дана таблица значений х и у.
Требуется:
1)Вычислить выборочные средние, выборочные дисперсии и средние квадратичные отклонения, выборочный коэффициент корреляции.
2) Записать выборочное уравнение линейной регрессии ух=ax+b. Вычислить остаточную дисперсию.
Решение. Здесь дана выборка объема n=5 из двумерной генеральной совокупности (Х, У).
1). Выборочные средние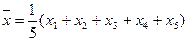 
, 
.
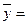
Выборочные дисперсии и среднеквадратичные отклонения
D 
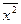= -( ) , D 
= 
-( 
) , 
, 
, где
= 
, = 
.
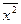Выборочный коэффициент корреляции
r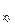 
= 
, где 
= 
(х у +х у +х 
у +х 
у 
+х 
у )
Коэффициент корреляции r 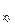любых двух случайных величин удовлетворяет неравенству 
r 
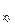
. Значения r 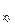близкие к нулю соответствуют отсутствию линейной связи между величинами х и у, а значения близкие по модулю к единице- тесной линейной связи между х и у.
2) Выборочное уравнение линейной регрессии
Последнее уравнение должно быть приведено к виду
ух=ax+b
Все расчеты удобно выполнять в табличной форме.
| n | x | y | x2 | y2 | xy | yx | (y- yx)2 |
| -2 | -2 | -0,33 | 2,79 | ||||
| 7,47 | 0,28 | ||||||
| 9,42 | 2,50 | ||||||
| 11,37 | 0,40 | ||||||
| 25,02 | 1,04 | ||||||
| 7,01 |
1) Для приведенной выборки = 3,6, = 10,6
D = 
17,84; D = 69,44
= 
=73
r = 
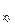0,99
2) Выборочное уравнение регрессии 
или
yх=1,95х+3,57.
По уравнению регрессии вычисляем ух и заполняют седьмой столбик таблицы.
Остаточная дисперсия вычисляется по формуле
Dост.= 
∑(y- yx)2= 
= 2,33