1.В процессе преобразования растрового графического изображения количество цветов уменьшилось с 65536 до 16. Во сколько раз уменьшится объем занимаемой им памяти?
2. В процессе преобразования растрового графического изображения количество цветов увеличилось с 16 до 42 949 67 296. Во сколько раз увеличился объем, занимаемый им в памяти?
3.Для хранения изображения размером 64x32 точек выделено 64 Кбайт памяти. Определите, какое максимальное число цветов допустимо использовать в этом случае.
4. Какой объем видеопамяти необходим для хранения двух страниц изображения при условии, что разрешающая способность дисплея равна 640 х 350 пикселей, а количество используемых цветов - 16?
5. Какой объем видеопамяти необходим для хранения четырех страниц изображения, если битовая глубина равна 24, а разрешающая способность дисплея - 800 х 600 пикселей?
6.. Сколько секунд потребуется модему, передающему сообщения со скоростью 28800 бит/с, чтобы передать цветное растровое изображение размером 640 х 480 пикселей, при условии, что цвет каждого пикселя кодируется тремя байтами? (ЕГЭ_2005, уровень В)
Системы счисления
Решение задач
| 1. | Сколько единиц в двоичной записи десятичного числа 194,5? | ||||||||
| 1) | 2) | 3) | 4) |
Решение:
1. Представим целую часть числа в двоичной системе счисления. 
 19410 = 110000102
19410 = 110000102
- Представим дробную часть числа в двоичной системе счисления.
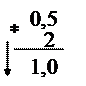
0,510=0,12
Таким образом, 194,510=11000010,12. В двоичной записи 4 единицы.
Ответ: 4
| 2. Дано А = 2478, B = A916. Какое из чисел C, записанных в двоичной системе, отвечает условию A < C < B? | ||||
| 1) С = 101010002 | 2) С = 101010102 | 3) С = 101010112 | 4) С = 101011002 | |
| Решение: Для сравнения необходимо представить числа в одной системе счисления, в данном случае двоичной, т. к. варианты ответа – двоичные числа. Для этого каждую цифру восьмеричного числа заменим триадой (группой из 3 двоичных цифр): 2478® 10100111 2. Аналогично переведем шестнадцатеричное число, заменяя цифры четверкой двоичных цифр: A916® 10101001 2. Далее приступаем к сравнению: 1) 101001112 < 101010002 и 101010002 < 101010012 (A < C < B). (на этом можно остановиться, т.к. решение найдено.) 2) 101001112 < 101010102 и 101010102 > 101010012 (A < B < C). 3) 101001112 < 101010112 и 101010112 > 101010012 (A < B < C). 4) 101001112 < 101011002 и 101011002 > 101010012 (A < B < C). Ответ: 1 Возможен способ решения, при котором сначала все числа переводятся в десятичную систему счисления, а затем сравниваются: 2478 =2 ∙ 82+4 ∙ 8+7=16710, A916=10 ∙ 16+9=16910. 1) 101010002=1 ∙ 27+1 ∙ 25+1 ∙ 23=16810 (A < C < B). 2) 101010102=1 ∙ 27+1 ∙ 25+1 ∙ 23+1 ∙ 2=17010 (A < B < C). 3) 101010112=1 ∙ 27+1 ∙ 25+1 ∙ 23+1 ∙ 2+1=17110 (A < B < C). 4) 101011002=1 ∙ 27+1 ∙ 25+1 ∙ 23+1 ∙ 22=17210 (A < B < C). | ||||
|
|
3. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 17 оканчивается на 2.
Решение.
Последняя цифра в записи числа представляет собой остаток от деления числа на основание системы счисления 17-2 = 15. Найдем делители числа 15, это числа 3, 5,15.
Выполним проверку, записав число 17 в системах счисления с основанием 3, 5, 15:
1710 = 1223 = 325 = 1215.
Ответ: 3, 5, 15.
Задачи для самостоятельного решения
1.Сколько значащих нулей содержится в двоичной записи суммы чисел а = 1058 и
b = С616?
1) 3 2) 4 3) 2 4) 5.
2. (Задание А1 демоверсии 2010 года (сайт fipi.ru))
Дано А=9D16, B=2378. Какое из чисел C, записанных в двоичной системе, отвечает условию A<C<B?
|
|
| 1) 10011010 | |
| 2) 10011110 | |
| 3) 10011111 | |
| 4) 11011110 |
3. Решение неравенств.
Поставьте вместо знака? знак <, > или =.
- 28510? 11D16
- 1111112? 11118
- 6С16? 1010012
- 5516? 1258
4. Расположите числа, записанные в различных системах счисления, в порядке возрастания:
3510, 368, 3А16, 1001012
5.. Перевести данное число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
а) 666(10); б) 305(10); в) 153,25(10);
6.. Перевести данное число в десятичную систему счисления.
а) 1100111011(2); в) 10110101,1(2); д) 671,24(8); е) 41A,6(16).