I. Методика решения задач по курсу общей физики
Физические основы классической механики
Основные формулы
| Скорость мгновенная | 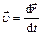
|
| Проекция мгновенной скорости на ось Ох | 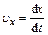
|
| Модуль скорости | 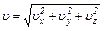
|
| Ускорение: - тангенциальное | 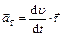
|
| - нормальное (центростремительное) | 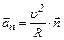
|
| - полное | 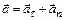 , , 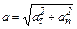
|
| Кинематическое уравнение прямолинейного равнопеременного движения в координатной форме | 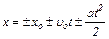
|
| Путь при равнопеременном движении | 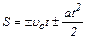
|
| Скорость равнопеременного движения | u = ±uo ± at |
| Угловая скорость | 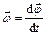
|
| Угловое ускорение | 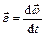
|
| Кинематическое уравнение равнопеременного движения материальной точки по окружности | 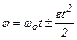
|
| Связь между линейными и угловыми величинами при вращательном движении | S = φR, u = wR, at = εR, an = w2R |
| Второй закон Ньютона | 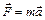 , , 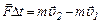
|
| Третий закон Ньютона | 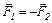
|
| Сила гравитационного взаимодействия | 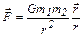
|
| Сила тяжести | 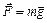
|
| Вес тела | 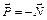
|
| Сила упругости | F = – kx |
| Сила трения скольжения | Fтр = mN |
| Закон сохранения импульса (количества движения) для замкнутой системы двух тел | 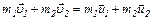
|
| Механическая работа постоянной силы | A = FS cos a |
| Мощность | N = A/t, N = Fu cos a |
| Кинетическая энергия тела при поступательном движении | 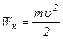
|
| Потенциальная энергия тела, поднятого над поверхностью Земли | WП = mgh |
| Потенциальная энергия упругодеформированного тела | 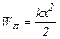
|
| Полная механическая энергия тела | E = Wк + WП |
| Момент инерции материальной точки | J = mr2 |
| Момент инерции тел массой m относительно оси, проходящей через центр масс: – тонкостенного цилиндра (кольца), обруча радиусом R, если ось вращения совпадает с геометрической осью | J = mR2 |
| – сплошного цилиндра (диска) радиусом R, если ось вращения совпадает с осью цилиндра | 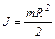
|
| – однородного стержня длиной l, если ось вращения перпендикулярна стержню | 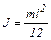
|
| – однородного шара радиусом R | 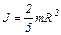
|
| Момент инерции однородного стержня длиной l, если ось вращения перпендикулярна стержню и проходит через один из его концов | 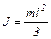
|
| Момент силы | 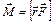 или М = F l или М = F l
|
| Основной закон динамики вращательного движения | 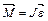
|
| Момент импульса вращающегося тела относительно оси | 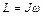
|
| Закон сохранения момента импульса (момента количества движения) для замкнутой системы двух тел | 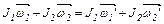
|
| Закон изменения момента импульса | 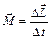
|
| Кинетическая энергия вращающегося тела | 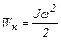
|
Примеры решения задач
Пример 1. Уравнение движения тела вдоль оси Ох имеет вид:
x = 2 + 15 t + 0,4 t2 + 6 t3. Найти: начальную координату хо; координату х, скорость u и ускорение а тела в момент времени t = 2 с; путь, пройденный за 2 с после начала движения.
| Дано: x = 2 + 15 t + 0,4 t2 + 6 t3; t = 2 с. Найти: х0; хt = 2 с; S; ut = 2 с; аt = 2 с. |  Рис. 1 Рис. 1
|
Решение: На рис. 1 показаны начальнаяи конечная координаты, векторы скорости 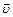 и ускорения
и ускорения 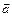 тела, движущегося прямолинейно вдоль оси Ох.
тела, движущегося прямолинейно вдоль оси Ох.
Из уравнения движения тела определим его начальную и конечную координаты: хo = 2 м, хt= 2 с = 81,6 м.
Пройденный путь равен разности значений координат хt = 2 си хo:
S = хt = 2 с – хo. (1)
Отсюда S = 79,6 м.
Мгновенную скорость в произвольный момент времени найдём, продифференцировав координату х по времени:
u = x' = 15 + 0,8 t + 18 t2. (2)
Мгновенное ускорение в произвольный момент времени – производная от скорости по времени:
a = u' = 0,8 + 36 t. (3)
В соответствии с (2) и (3) для момента времени t =2 с:
ut =2с = (15+0,8×2 +18×22) м/с = 88,6 м/с, аt =2с = (0,8 + 36×2) м/с2 = 72,8 м/с2.
Ответ: хo = 2 м; хt =2 с = 81,6 м; S = 79,6 м; ut =2 с = 88,6 м/с; аt =2 с = 72,8 м/с2.
Пример 2. Колесо радиусом R = 50 см вращается равноускоренно
с ускорением ε = 1,26 с-2. Найти линейную скорость u, нормальное аn и тангенциальное аt ускорения точек обода колеса через время t = 20 с после начала вращения.
| Дано: wо = 0; ε = 1,26 с-2; R = 50 см= 0,5 м; t = 20 с. Найти: u; аn; аt. |  Рис. 2 Рис. 2
|
Решение: На рис. 2 изображены векторы, характеризующие вращение колеса по часовой стрелке, в произвольный момент времени. Направления векторов скорости 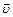 и тангенциального ускорения
и тангенциального ускорения 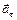 совпадают с касательной в каждой точке колеса. Вектор нормального ускорения
совпадают с касательной в каждой точке колеса. Вектор нормального ускорения 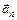 перпендикулярен вектору скорости
перпендикулярен вектору скорости 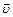 и направлен по радиусу к центру колеса. Вектор
и направлен по радиусу к центру колеса. Вектор 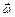 направлен в соответствии с правилом правого винта перпендикулярно плоскости рисунка, от нас. При равноускоренном вращении направление вектора углового ускорения
направлен в соответствии с правилом правого винта перпендикулярно плоскости рисунка, от нас. При равноускоренном вращении направление вектора углового ускорения  совпадает с направлением угловой скорости
совпадает с направлением угловой скорости 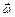 [1].
[1].
Согласно определению угловая скорость w равноускоренного вращательного движения
w =wo+ ε t.
Поскольку wo = 0, то
w = ε t. (1)
Линейная скорость колеса связана с его угловой скоростью
u = w R. (2)
Подставив (1) в (2), получим
u = ε R t. (3)
Откуда u = 1,26∙0,5∙20 м/с = 12,6 м/с.
Нормальное (центростремительное) ускорение находим по формуле
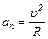 . (4)
. (4)
Следовательно, 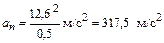 .
.
Тангенциальное (касательное) ускорение
at = ε R. (5)
Числовое значение at = 12,6∙0,5 м/c2 = 0,63 м/с2.
Ответ: u = 12,6м/с; an = 317,5 м/с2; at = 0,63 м/с2.
Пример 3. На гладкой горизонтальной плоскости находится тело массой m1 = 250 г. Тело массой m2 = 400 г подвешено на невесомой и нерастяжимой нити, перекинутой через блок и привязанной к телу массой m1. Пренебрегая массой блока и трением, определить силу натяжения нити Fнат; ускорение а тел; путь S, пройденный телами за время
t = 0,2 с.
| Дано: m1 = 250 г = 0,25 кг; m2 = 400 г = 0,4 кг; t = 0,2 с. Найти: Fнат; а; St = 0,2 с. | 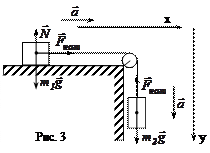
|
Решение: На рис. 3 показаны силы, действующие на тела m1 и m2: 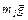 и
и 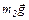 – силы тяжести,
– силы тяжести, 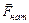 – сила натяжения нити,
– сила натяжения нити, 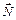 – сила нормальной реакции опоры.
– сила нормальной реакции опоры.
Из условия невесомости и нерастяжимости нити следует, что сила натяжения нити на всех участках одинакова и грузы движутся с одним и тем же ускорением.
Запишем второй закон Ньютона в векторной форме для обоих тел:
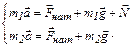 (1)
(1)
Выбираем направление осей Ох и Оy по направлению вектора ускорения 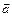 . Проецируем векторы на указанные оси, тогда второй закон Ньютона в скалярной форме примет вид:
. Проецируем векторы на указанные оси, тогда второй закон Ньютона в скалярной форме примет вид:
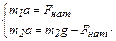 (2)
(2)
Отсюда
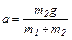 . (3)
. (3)
Числовое значение ускорения 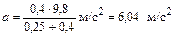 .
.
Из (2) вычислим значение силы натяжения Fнат = 0,25∙6,04 Н = 1,51 Н.
Учитывая, что uo = 0, путь при равноускоренном движении
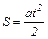 . (4)
. (4)
Таким образом, за время t = 0,2 с пройденный путь
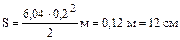 .
.
Ответ: Fнат = 1,51 Н; а = 6,04 м/с2; S = 12 см.
Пример 4. Человек массой m = 70 кг поднимается в лифте, движущемся равномерно (а1 = 0). Определить вес человека Р1. Во сколько раз изменится его вес, если лифт поднимается с ускорением а2 = 1 м/с2?
| Дано: m = 70 кг; а1 = 0; а2 = 1 м/с2. Найти: Р1; Р2 / Р1. | 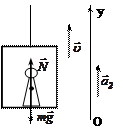 Рис. 4
Рис. 4
|
Решение: На человека, находящегося в движущемся лифте, действуют сила тяжести 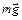 и сила упругости (сила реакции пола)
и сила упругости (сила реакции пола) 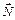 . Записываем второй закон Ньютона в векторной форме:
. Записываем второй закон Ньютона в векторной форме:
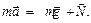 (1)
(1)
В скалярной форме
ma = - mg +N. (2)
При равномерном подъёме (ускорение а1 = 0) уравнение (2) примет вид
N1 = mg, (3)
где N1 – сила реакции опоры, действующая на человека, поднимающегося в лифте равномерно.
На основании третьего закона Ньютона вес человека равен силе реакции опоры
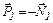 . (4)
. (4)
Вес 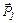 приложен к опоре и направлен противоположно
приложен к опоре и направлен противоположно 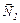 . Из (3) и (4) получаем:
. Из (3) и (4) получаем:
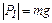 . (5)
. (5)
При равномерном подъёме Р1 = 700 Н.
При равноускоренном подъёме (а2 = 1 м/с2) уравнение (2) запишем в виде
ma2 = – mg + N2, (6)
где N2 – сила реакции опоры при подъёме с ускорением.
Откуда
N2 = m(g +a2). (7)
Вес тела при равноускоренном подъёме
Р2 = N2 = m(g +a2). (8)
Отношение 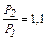 .
.
Ответ: Р1 = 700 Н, при подъёме с ускорением вес тела увеличится в 1,1 раза.
Пример 5. Геостационарный искусственный спутник Земли "висит" над одной точкой экватора и делает полный оборот вокруг Земли за время Т = 24 часа (рис. 5). На какую высоту запущен спутник? Каковы скорость и ускорение его движения на данной высоте? Радиус Земли
R = 6370 км.
| Дано: R = 6370 км = 6,37∙106 м; Т = 24 ч = 8,64∙104 с; go = 9,8 м/с2. Найти: H; u; g. | 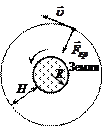 Рис. 5
Рис. 5
|
Решение: Поскольку на спутник действует только гравитационная сила, то второй закон Ньютона для спутника имеет вид
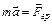 , (1)
, (1)
где 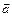 – центростремительное ускорение,
– центростремительное ускорение, 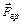 – сила притяжения Земли,
– сила притяжения Земли,
m – масса спутника.
Центростремительное ускорение находим по формуле
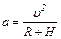 . (2)
. (2)
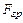 определим из закона всемирного тяготения
определим из закона всемирного тяготения
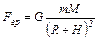 , (3)
, (3)
где М – масса Земли.
Подставляя (2) и (3) в (1), получим:
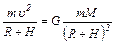 .
.
Отсюда 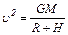 . (4)
. (4)
На основании формулы (3) ускорение свободного падения у поверхности Земли
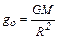 . (5)
. (5)
Преобразуем (5)
GM = goR2. (6)
С учётом (6) выражение (4) принимает вид
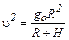 . (7)
. (7)
При равномерном вращении с периодом Т скорость спутника
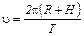 . (8)
. (8)
Из формул (7) и (8) находим высоту спутника Н над Землей
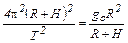 .
.
Откуда
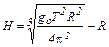 . (9)
. (9)
Следовательно, Н = 35930 км.
Зная Н, по формуле (8) находим u = 3,07 км/с.
Ускорение спутника равно ускорению силы тяжести на высоте Н
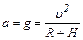 . (10)
. (10)
Соответственно g = 0,22 м/с2.
Ответ: Н = 35930 км; u = 3,07 км/с; g = 0,22 м/с2.
Пример 6. Какую силу F1 нужно приложить к середине бревна в точке А (рис. 6а), чтобы закатить его на ступеньку высотой, равной
0,5 радиуса бревна? Во сколько раз сила F2, позволяющая приподнять бревно на высоту ступеньки, больше силы F1? Масса бревна m = 50 кг.
| Дано: h = ½ R; m = 50 кг. Найти: F; F2 /F1. | 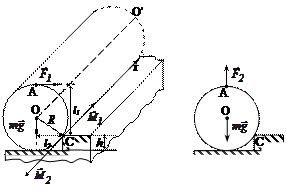 а) б)
Рис. 6 а) б)
Рис. 6
|
Решение: При закатывании бревна на ступеньку сила 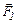 и сила тяжести
и сила тяжести 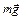 создают вращающие моменты
создают вращающие моменты 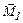 и
и 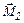 . Направления векторов
. Направления векторов 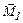 и
и 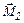 определяются по правилу правого винта (рис. 6а).
определяются по правилу правого винта (рис. 6а).
Модуль момента силы F1 относительно точки С
M1 = F 1 l1, (1)
где 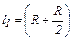 – плечо силы F1.
– плечо силы F1.
Таким образом,
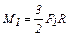 . (2)
. (2)
Модуль момента силы тяжести относительно точки С
M2 = m g l2, (3)
где l2 – плечо силы тяжести.
По теореме Пифагора находим плечо силы тяжести
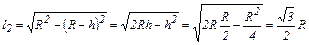 . (4)
. (4)
Условием перекатывания бревна будет равенство моментов М1 и М2, то есть
m g l2 = F1 l1 (5)
или
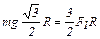 . (6)
. (6)
Откуда
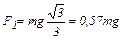 . (7)
. (7)
После расчёта получим: F1 = 0,57∙500 Н = 288,7 Н.
При поднятии груза равномерно вверх сила 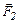 преодолевает силу тяжести
преодолевает силу тяжести 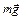 (рис. 6б). По второму закону Ньютона в скалярной форме
(рис. 6б). По второму закону Ньютона в скалярной форме
F2 = mg. (8)
Отсюда F2 = 50∙10 Н = 500 Н.
Ответ: F1 = 288,7 Н; F2 / F1 = 1,73, т.е. бревно легче закатить на ступеньку, чем поднять на высоту самой ступеньки.
Пример 7. Молотильный барабан, момент инерции которого
J = 30 кг∙м2, вращается с частотой no = 20 с-1. Определить момент силы, под действием которого барабан остановится за время ∆ t = 3,3 мин.
| Дано: no = 20 с-1; n = 0; ∆t = 3,3 мин = 198 c; J = 30 кг∙м2. Найти: Mтр. |
 Рис. 7 Рис. 7
|
Решение: На рис. 7 указаны направления векторов, характеризующих равнозамедленное вращение барабана. Замедленное вращение барабана совершается под действием постоянного тормозящего момента 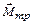 .
.
Согласно закону изменения момента импульса произведение момента силы, действующего на барабан, и времени действия этого момента, равно изменению момента импульса барабана:
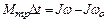 , (1)
, (1)
где wо и w – начальная и конечная угловые скорости.
В момент остановки w = 0, поэтому 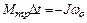 .
.
Отсюда
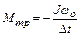 . (2)
. (2)
Поскольку угловая скорость связана с частотой вращения соотношением
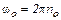 , (3)
, (3)
то получаем расчётную формулу для тормозящего момента
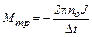 . (4)
. (4)
Следовательно, 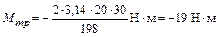 .
.
Знак минус показывает, что момент силы трения оказывает тормозящее действие.
Ответ: Мтр = –19 Н∙м.
Пример 8. На спокойной воде пруда стоит лодка длиной L и массой m2 перпендикулярно берегу, обращённая к нему носом. На носу лодки стоит человек массой m1. На какое расстояние S лодка приблизится к берегу, если человек перейдёт с носа на корму лодки (рис. 8).
| Дано: L; m1; m2. Найти: S. |  Рис. 8
Рис. 8
|
Решение: Считаем, что человек идёт по лодке с постоянной скоростью. Лодка в этом случае также будет двигаться равномерно, но в противоположную сторону. При движении импульс человека
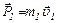 , (1)
, (1)
где 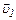 – скорость человека относительно берега.
– скорость человека относительно берега.
Импульс лодки
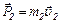 , (2)
, (2)
где 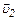 – скорость лодки относительно берега.
– скорость лодки относительно берега.
В системе отсчёта, связанной с берегом, скорость лодки
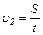 . (3)
. (3)
Учитывая, что человек движется относительно лодки и вместе с лодкой, скорость человека относительно берега
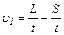 . (4)
. (4)
Система "лодка-человек" является замкнутой, так как внешние силы (сила тяжести и выталкивающая сила) скомпенсированы. Для замкнутой системы тел справедлив закон сохранения импульса. Поскольку до начала перемещения человека импульс системы равен нулю, то закон сохранения импульса запишем в виде
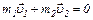 . (5)
. (5)
Проецируем импульсы 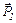 и
и 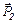 на ось ох и учитываем (3) и (4):
на ось ох и учитываем (3) и (4):
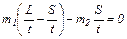 . (6)
. (6)
Получаем искомую расчётную формулу
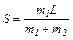 . (7)
. (7)
Ответ: 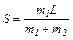 .
.
Пример 9. На краю горизонтальной платформы, имеющей форму диска, стоит человек массой m2 = 80 кг. Масса платформы m1 = 240 кг, её радиус R = 2 м. Платформа может вращаться вокруг вертикальной оси, проходящей через её центр. Пренебрегая трением, найти, с какой частотой будет вращаться платформа, если человек пойдёт вдоль её края со скоростью u =1 км/ч.
| Дано: m1 = 240 кг; m2 = 80 кг; u = 1 км/ч = 0,28 м/с; R = 2 м. Найти: n1. |  Рис. 9
Рис. 9
|
Решение: Система "человек – платформа"является замкнутой, так как моменты внешних сил (силы тяжести и силы реакции опоры), действующих на эту систему относительно оси ОО¢, являются уравновешенными. Для такой системы выполняется закон сохранения момента импульса
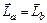 , (1)
, (1)
где 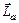 и
и 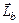 – моменты импульсов системы до и после начала движения человека по платформе соответственно.
– моменты импульсов системы до и после начала движения человека по платформе соответственно.
До начала движения человека момент импульса системы относительно неподвижной оси ОО', связанной с полом,
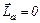 . (2)
. (2)
При движении человека вдоль края платформы момент импульса всей системы
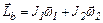 , (3)
, (3)
где J1 и J2 – моменты инерции платформы и человека, 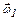 и
и 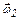 – их угловые скорости относительно ОО¢.
– их угловые скорости относительно ОО¢.
Угловые скорости 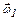 и
и 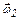 направлены в противоположные стороны, так как при движении человека платформа вращается в противоположном направлении.
направлены в противоположные стороны, так как при движении человека платформа вращается в противоположном направлении.
На рис. 9 показаны векторы моментов импульсов платформы 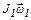 и человека
и человека 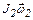 .
.
Момент инерции платформы находим по формуле
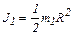 . (4)
. (4)
Считая, что масса человека сосредоточена в точке касания с платформой, его момент инерции
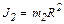 . (5)
. (5)
Человек движется относительно платформы и вместе с ней, поэтому его угловая скорость относительно оси ОО¢, связанной с полом,
w2 = (wo2 – w1), (6)
где 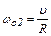 – угловая скорость человека относительно платформы.
– угловая скорость человека относительно платформы.
Следовательно,
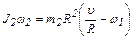 . (7)
. (7)
Согласно закону сохранения момента импульса (1) для системы "человек – платформа" и формулам (2), (3)
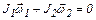 . (8)
. (8)
Спроецируем векторы 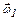 и
и 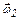 на ось ОО':
на ось ОО':
I1w1 – I2w2 = 0.
С учётом выражений (4) и (8) имеем
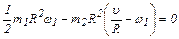 . (9)
. (9)
Отсюда
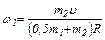 . (10)
. (10)
Используя связь между угловой скоростью w и частотой n
(w = 2 π n), получим формулу для частоты вращения платформы n1:
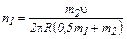 . (11)
. (11)
Подставив числовые значения в (11), найдём
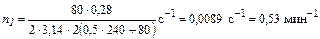 .
.
Ответ: n1 = 0,53 мин–1.
Пример 10. Молот массой m = 200 кг падает с высотой h = 20 см на заготовку, масса которой вместе с наковальней составляет М = 2500 кг. Найти: кинетическую энергию молота в момент удара Wк1; энергию Wк2, переданную системе "молот – заготовка – наковальня"; полезную энергию, необходимую для деформации заготовки Е д; коэффициент полезного действия удара η. Удар молота о заготовку рассматривать как неупругий.
| Дано: m = 200 кг; M = 2500 кг; h = 20 см = 0,2 м. Найти: Wк1; Wк2; Е д; η. |
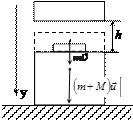 Рис. 10 Рис. 10
|
Решение: Если пренебречь силами сопротивления, то систему "молот– Земля" можно считать замкнутой. Падение молота происходит под действием силы тяжести, следовательно, к системе "молот – Земля" можно применить закон сохранения механической энергии. Потенциальная энергия молота mgh в конце падения с высоты h переходит в его кинетическую энергию Wк1.
mgh= Wк1. (1)
Подставляя числовые значения, получаем: Wк1 = 200∙10∙0,2 Дж = 400 Дж.
Система "молот – заготовка – наковальня" является замкнутой, но неконсервативной, поэтому можно считать, что энергия, затраченная на деформацию заготовки, равна разности значений механических энергий до и после удара. Во время удара изменяется только кинетическая энергия тел, так как незначительным перемещением тел по вертикали во время удара пренебрегаем. Тогда полезная энергия, затраченная на деформацию (ковку),
Е д = Wк1 – Wк2, (2)
где Wк2 – кинетическая энергия системы после удара.
Для определения кинетической энергии, переданной системе, необходимо знать её скорость после удара. Применим закон сохранения импульса для этой системы в момент удара:
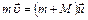 , (3)
, (3)
где 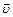 – скорость молота до удара,
– скорость молота до удара, 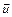 – скорость наковальни, заготовки и молота после удара.
– скорость наковальни, заготовки и молота после удара.
Уравнение (3) запишем в скалярной форме
mu = (m+M) u. (4)
Отсюда
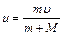 . (5)
. (5)
Кинетическая энергия системы после удара
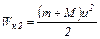 . (6)
. (6)
Из выражений (5) и (6) получим формулу для Wк2:
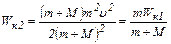 . (7)
. (7)
Отсюда 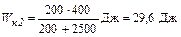 .
.
Согласно формуле (2) энергия, затраченная на деформацию (ковку), Е д = (400 – 29,6) Дж = 370,4 Дж.
Коэффициент полезного действия определим как отношение полезной энергии, затраченной на деформацию, к полной энергии Wк1:
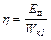 . (8)
. (8)
Соответственно, кпд 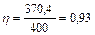 или η = 93%.
или η = 93%.
Ответ: Wк1 = 400 Дж; Wк2 = 29,6 Дж; Е д = 370,4 Дж; η = 93 %.
Пример 11. Шар, катившийся со скоростью u1 = 3 м/с, ударился о стену и покатился назад со скоростью u2 = 2 м/с (рис. 11). Масса шара m = 3 кг. На сколько изменилась кинетическая энергия шара? Какая часть энергии шара перешла во внутреннюю энергию стены?
| Дано: m = 3 кг; u1 = 3 м/с; u2 = 2 м/с. Найти: ∆ Wк;∆ Wк / Wк1. |
 Рис. 11 Рис. 11
|
Решение: Кинетическая энергия шара при качении складывается из кинетической энергии поступательного и вращательного движения.
Кинетическая энергия поступательного движения
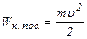 , (1)
, (1)
где u – скорость поступательного движения центра масс шара.
Кинетическая энергия вращательного движения
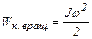 , (2)
, (2)
где w – угловая скорость вращения относительно центра масс.
Момент инерции шара
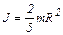 . (3)
. (3)
Линейная u и угловая w скорости связаны соотношением
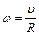 . (4)
. (4)
Используя формулы (1), (2), (3) и (4), выразим кинетическую энергию катящегося шара
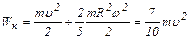 . (5)
. (5)
Кинетические энергии шара до и после удара соответственно равны:
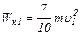 и
и 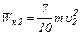 .
.
Изменение кинетической энергии
∆ Wк = Wк2 – Wк1. (6)
Подставив в (6) выражения для Wк1 и Wк2 , получим
.
Отсюда ∆ Wк = 0,7∙3∙(22 – 32) Дж = –10,5 Дж. Знак "–" указывает на уменьшение кинетической энергии.
Во внутреннюю энергию, связанную с неупругой деформацией стенки, перешла энергия ∆Wк.
Вычислим кинетическую энергию шара до удара:
Wк1 = 0,7×3×32 Дж = 18,9 Дж
Следовательно: 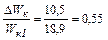 или
или 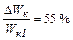 .
.
Ответ: ∆ Wк = –10,5 Дж; 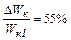 .
.
Молекулярная физика. Термодинамика
Основные законы и формулы
| Уравнение состояния идеального газа (уравнение Клапейрона–Менделеева) | pV = nRT |
| Масса молекулы | m0 = M/NA |
| Количество вещества | ν = m/ M, ν = N / NA |
| Средняя кинетическая энергия молекулы | 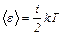
|
| Основное уравнение молекулярно-кине-тической теории | 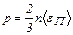
|
| Внутренняя энергия идеального газа | 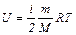
|
| Наиболее вероятная скорость | 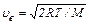
|
| Средняя квадратичная скорость молекулы | 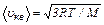
|
| Средняя арифметическая скорость молекулы | 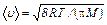
|
| Количество теплоты, необходимое для нагревания тела | Q = c×m ×∆ T |
| Удельная теплоёмкость газа при постоянном объёме | 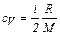
|
| Удельная теплоёмкость газа при постоянном давлении | 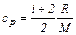
|
| Среднее число соударений молекулы в единицу времени | 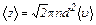
|
| Средняя длина свободного пробега молекулы | 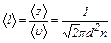
|
| Закон диффузии (закон Фика) | 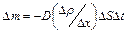
|
| Закон теплопроводности (закон Фурье) | 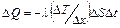
|
| Работа газа при изобарном расширении | 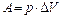
|
| Работа газа при изотермическом расширении | 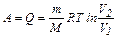
|
| Работа газа при адиабатном расширении | 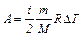
|
| Уравнения адиабатного процесса (уравнения Пуассона) | 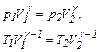
|
| Изменение энтропии | 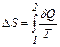
|
| Термический КПД тепловой машины | η = (Q1–Q2) / Q1 |
| Термический КПД идеальной тепловой машины (цикла Карно) | η = (T1–T2) / T1 |
| Высота подъёма жидкости в капиллярной трубке | 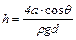
|
Примеры решения задач
Пример 1. Определить число атомов N, содержащихся в 1 кг гелия. Найти массу m0 одного атома гелия.
| Дано: m = 1 кг; М = 4·10-3 кг/моль. Найти: N; mo. |
Решение: Поскольку гелий – одноатомный газ, то число атомов в данной массе газа
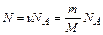 , (1)
, (1)
где n = m /М – количество молей вещества, М – молярная масса, m – масса газа, NА – число Авогадро.
Найдём искомое число атомов 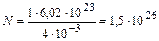 .
.
Для определения массы m0 одного атома массу m газа разделим на число атомов N в нём: 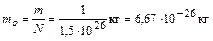 .
.
Ответ: N = 1,5·1026; mo = 6,67·10–26 кг.
Пример 2. Считая водород в солнечной фотосфере (внешней видимой оболочке Солнца) идеальным газом, определить среднюю кинетическую энергию 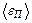 поступательного движения атомов водорода. Концентрация атомов водорода в фотосфере n = 1,6∙1021 м–3, давление
поступательного движения атомов водорода. Концентрация атомов водорода в фотосфере n = 1,6∙1021 м–3, давление
Р = 1,25∙102 Па.
Дано: n = 1,6∙1021 м–3;
Р = 1,25∙102 Па.
Найти: 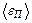 . .
|
Решение: Связь между давлением р идеального газа, концентрацией n и средней кинетической энергиейтеплового движения частиц 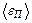 выражается основным уравнением молекулярно-кинети-ческой теории:
выражается основным уравнением молекулярно-кинети-ческой теории:
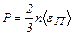 , (1)
, (1)
Отсюда
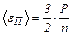 . (2)
. (2)
Следовательно, 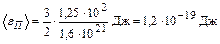 .
.
Ответ: 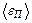 = 1,2∙10–19 Дж.
= 1,2∙10–19 Дж.
Пример 3. Найти наиболее вероятную υв, среднюю арифметическую 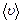 и среднюю квадратичную
и среднюю квадратичную 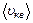 скорости молекул водорода при температуре 27 oС.
скорости молекул водорода при температуре 27 oС.
Дано: t = 27 oC; Т = 300 К;
МН2 = 2∙10-3 кг/моль.
Найти: υв; 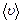 ; ; 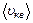 . .
|  Рис. 1 Рис. 1
|
Решение: В газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется статистическому распределению Максвелла.
Распределение Максвелла (рис. 1) позволяет определить относительное число молекул ∆ N(υ)/N, скорости которых лежат в интервале от υ до υ+∆υ.
Скорость υв, которой соответствует максимум кривой распределения Максвелла, называют наиболее вероятной скоростью. Этой скоростью и близкой к ней при данной температуре обладает наибольшее число молекул.
Наиболее вероятную скорость найдем по формуле
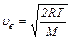 , (1)
, (1)
где R – молярная газовая постоянная, Т – абсолютная температура,
М – масса одного моля газа.
Произведём вычисления: 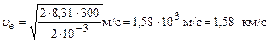 .
.
Средняя арифметическая скорость 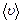 по определению равна отношению суммы скоростей всех молекул к числу молекул:
по определению равна отношению суммы скоростей всех молекул к числу молекул:
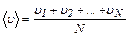 . (2)
. (2)
Из закона распределения Максвелла средняя арифметическая скорость молекул определяется следующим образом:
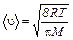 . (3)
. (3)
Следовательно, 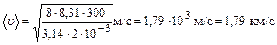 .
.
Если газ в объёме V содержит N молекул, движущихся со скоростями u1, u2,..., uN, то средняя квадратичная скорость
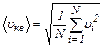 . (4)
. (4)
Средняя квадратичная скорость 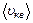 определяет среднюю кинетическую энергию движения молекулы. Средняя кинетическая энергия поступательного движения
определяет среднюю кинетическую энергию движения молекулы. Средняя кинетическая энергия поступательного движения 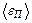 связана с температурой Т формулой
связана с температурой Т формулой
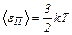 . (5)
. (5)
С другой стороны 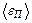 может быть определена по формуле
может быть определена по формуле
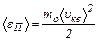 . (6)
. (6)
Сравнивая (5) и (6), находим