Задание 8.1. Решить задачу на определение вероятности случайного события.
8.1.1 Студент разыскивает нужную ему формулу в трёх справочниках. Вероятности того, что формула содержится в первом, во втором и в третьем справочниках соответственно равны: 0,6; 0,7; 0,8. Найти вероятность того, что нужная формула окажется: а) только в одном справочнике; б) хотя бы в одном справочнике; в) во всех справочниках.
8.1.2 Рабочий обслуживает 3 станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02; для второго – 0,03; для третьего – 0,04. Производительность первого станка в два раза больше, чем второго и в три раза меньше, чем третьего. Определить вероятность того, что взятая наудачу деталь изготовлена на третьем станке, если известно, что она годная.
8.1.3 На искусственном спутнике Земли установлено два различных прибора для измерения одной и той же величины. Для первого вероятность его безотказной работы в течении месяца равна 0,9; для второго – 0,7. Определить вероятности следующих событий: а) все приборы выйдут из строя в течении месяца; б) один прибор выйдет из строя; в) ни один прибор не выйдет из строя.
8.1.4 В трех группах была проведена контрольная работа. В первой группе из 15 человек трое написали на 5, во второй группе из 20 человек четверо написали на 5, в третьей группе из 22 человек двое написали на 5. Какова вероятность того, что случайно отобранная отличная работа написана студентом из второй группы?
8.1.5 Петя купил по одному лотерейному билету трех различных лотерей. Вероятности хоть какого-либо выигрыша в этих лотереях соответственно равны: 0,2; 0,3; 0,25. Найти вероятность того, что у Пети: а) все билеты выигрышные; б) только один билет выигрышный; в) хотя бы один билет выигрышный.
|
|
8.1.6 Станок обрабатывает 3 вида деталей, причем все его время распределяется между ними в отношении 1: 5: 4. При обработке детали 1-го вида он работает с максимальной для него нагрузкой в течение 70% времени, при обработке детали 2-го вида – в течение 50% и 3-его – 20% времени. В случайно выбранный момент времени станок работал с максимальной нагрузкой. Определить вероятность того, что он в это время обрабатывал деталь 2-го вида.
8.1.7 В студии 3 телекамеры. Для первой камеры вероятность того, что она включена в данный момент, равна 0,7; для второй – 0,8; для третьей – 0,6. Найти вероятность того, что в данный момент: а) включены все камеры; б) включена только одна камера; в) включена хотя бы одна камера.
8.1.8 Не склад поступает продукция трёх фабрик. Первая фабрика поставляет 1000 изделий, вторая – 2500, третья – 1500. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй – 2%, для третьего – 1%. Найти вероятность того, что наудачу взятое изделие произведено на первой фабрике, если оно оказалось стандартным.
8.1.9 Четыре стрелка стреляют по мишени. Вероятность попадания в «десятку» для первого стрелка равна 0,7; для второго – 0,8; для третьего – 0,6, для четвертого – 0,9. Какова вероятность того, что при одновременном залпе: а) в «десятку» попадет только один стрелок; б) никто не попадет в «десятку», в) хотя бы один попадет в «десятку».
8.1.10 В ОТК поступают детали с двух автоматов. С первого – 300 деталей, из них 250 годных; со второго 150 деталей, из них 120 годных. Найти вероятность того, что наудачу взятая деталь изготовлена первым автоматом, если она при проверке оказалась годной.
|
|
Задание 8.2. Решить задачу на определение вероятности случайного события.
8.2.1 Вероятность отказа каждого прибора при испытании равна 0,2. Приборы испытываются независимо друг от друга. Что вероятнее: отказ 10 приборов из 80, или отказ 15 при испытании 120?
8.2.2 Отмечено, что в городе N, в среднем, 10% заключенных браков в течении года заканчиваются разводом. Какова вероятность того, что из 8 случайно отобранных пар, заключивших брак, в течении года: а) ни одна пара не разведется; б) разведутся 2 пары?
8.2.3 Вероятность дозвониться в справочную вокзала равна 0,7. Найти вероятность того, что из 100 абонентов не менее 68 дозвонятся до справочной.
8.2.4 Вероятность выигрыша по облигации равна 0,25. Найти вероятность того, что из 8 облигаций выиграют не менее 2?
8.2.5 Вероятность «сбоя» в работе рации при каждом вызове равна 0,1. Поступило 112 вызовов. Определить вероятность не более 15 «сбоев».
8.2.6 Тест содержит 8 вопросов, на которые следует отвечать, используя одно из двух слов: да, нет. Какова вероятность получить не менее 6 правильных ответов?
8.2.7 Какова вероятность, что из 630 служащих компании не более ста родились в понедельник?
8.2.8 Бригада посадила 9 деревьев. Найти вероятность того, что приживутся не менее 7 деревьев, если вероятность приживания одного дерева равна 0,7.
8.2.9 Всхожесть семян составляет 90%. Чему равна вероятность того, что из 500 семян взойдут более 400?
8.2.10 Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность, что среди 9 случайно отобранных деталей непроверенными окажутся не более трех.
|
|
Задание 8.3. Дискретная случайная величина Х задана законом распределения. Требуется:
1) построить многоугольник распределения;
2) найти функцию распределения F (x) и построить ее график;
3) найти числовые характеристики случайной величины Х (математическое ожидание М (Х),дисперсию D (Х), среднее квадратическое отклонение σ (Х)).
| 8.3.1 |
| 8.3.2 |
| ||||||||||||||||||||
| 8.3.3 |
| 8.3.4 |
| ||||||||||||||||||||
| 8.3.5 |
| 8.7.6 |
| ||||||||||||||||||||
| 8.3.7 |
| 8.3.8 |
| ||||||||||||||||||||
| 8.3.9 |
| 8.3.10 |
|
Задание 8.4. Непрерывная случайная величина задана интегральной функцией распределения F (x). Требуется найти:
1) дифференциальную функцию распределения f (x) (плотность вероятности);
2) математическое ожидание М (Х);
3) дисперсию D (Х) и среднее квадратическое отклонение σ (Х);
4) вероятность попадания заданной случайной величины Х в заданный интервал P(α<X<β);
5) построить график интегральной функции распределения;
6) построить график дифференциальной функции распределения.
| 8.4.1 | 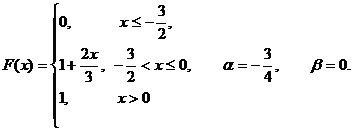
|
| 8.4.2 | 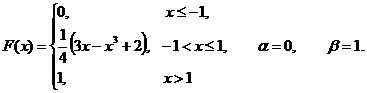
|
| 8.4.3 | 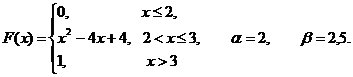
|
| 8.4.4 | 
|
| 8.4.5 | 
|
| 8.4.6 | 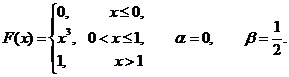
|
| 8.4.7 | 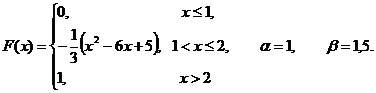
|
| 8.4.8 | 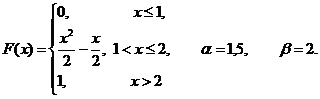
|
| 8.4.9 | 
|
| 8.4.10 | 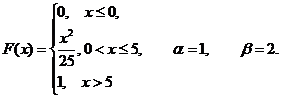
|