Для вычисления мгновенных значений при действии при действии источников сигнала e(t) и j(t) произвольной формы нужно упростить схему, исключив ток 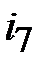 .
.
Рисунок 2 – Модель цепи для мгновенных значений при действии источников сигнала e(t) и j(t) произвольной формы
В результате модель цепи будет имеет 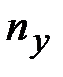 =4 узла,
=4 узла,  =7 ветвей,
=7 ветвей,  ;
;
 =
= 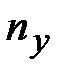 – 1 = 3 уравнения по первому закону Кирхгофа;
– 1 = 3 уравнения по первому закону Кирхгофа;
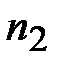 =
= 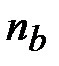 –
–  -
- 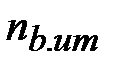 = 3 уравнения по второму закону Кирхгофа.
= 3 уравнения по второму закону Кирхгофа.
Количество уравнений должно быть равно количеству неизвестных токов:

Выбираем 3 узла и составляем уравнения по первому закону Кирхгофа:
Узел 1: 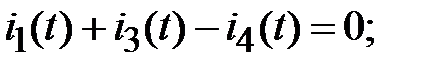
Узел 2: 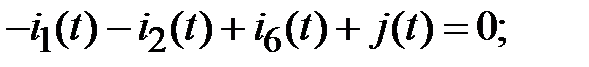
Узел 3: 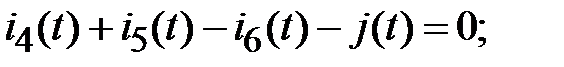
Для трех элементарных контуров составляем уравнения по второму закону Кирхгофа:
1к: 
2k: 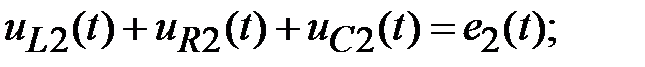
3k: 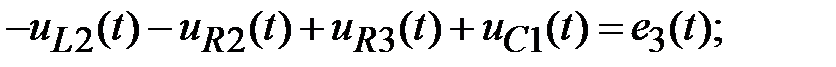
Введем компонентные уравнения для перехода к мгновенным значениям

После подстановки компонентных уравнений (КУ) получим систему, позволяющую найти токи ветвей:
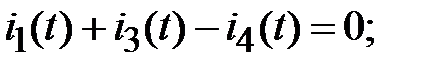
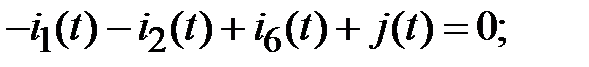
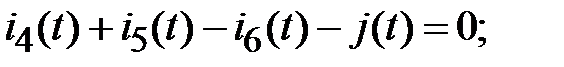
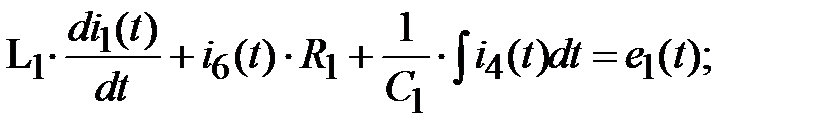
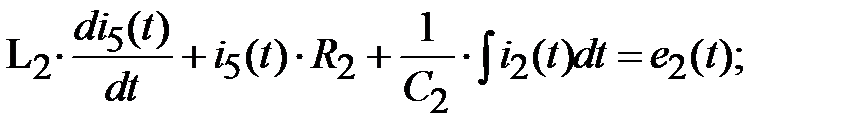
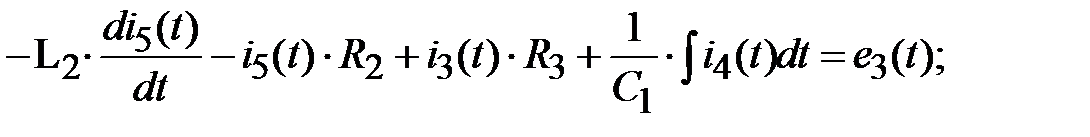
ММЦ для комплексных значений при действии источников гармонических сигналов
Рисунок 3 – Модель цепи для комплексных значений при действии источников гармонических сигналов
В результате модель цепи будет имеет 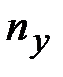 =4 узла,
=4 узла,  =7 ветвей,
=7 ветвей,  ;
;
 =
= 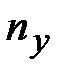 – 1 = 3 уравнения по первому закону Кирхгофа;
– 1 = 3 уравнения по первому закону Кирхгофа;
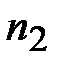 =
= 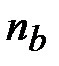 –
–  -
- 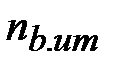 = 3 уравнения по второму закону Кирхгофа.
= 3 уравнения по второму закону Кирхгофа.
Количество уравнений должно быть равно количеству неизвестных токов:

Выбираем 3 узла и составляем уравнения по первому закону Кирхгофа:
Узел 1: 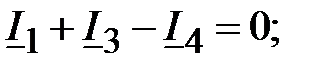
Узел 2: 
Узел 3: 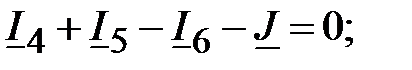
Для трех элементарных контуров составляем уравнения по второму закону Кирхгофа:
1к: 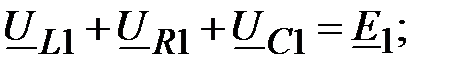
2k: 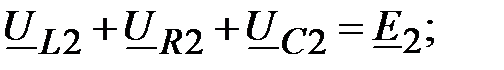
3k: 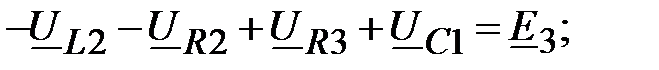
Преобразуем уравнения по второму закону Кирхгофа:
1к: 
2k: 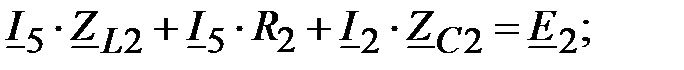
3k: 
Учтем, что
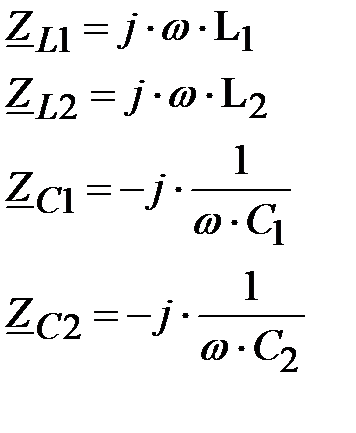
Получаем следующую систему уравнений:
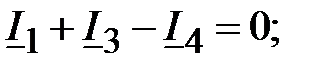

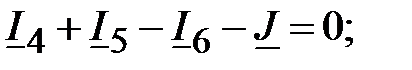
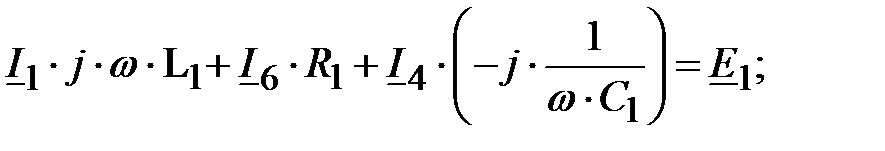
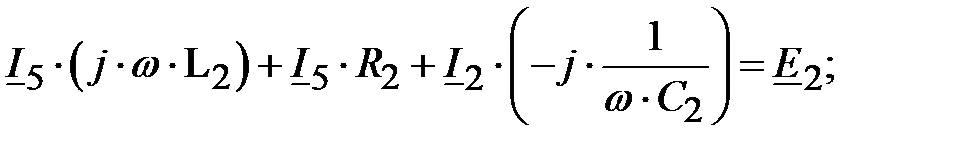

ММЦ для постоянных значений при действии источников постоянных сигналов
|
|
При действии источников постоянного сигнала, сопротивление катушки индуктивности становиться равным нулю, а сопротивление емкостного элемента – бесконечности. С учетом этого модель цепи имеет следующий вид:
Рисунок 4 – Модель цепи для постоянных значений при действии источников постоянных сигналов
Рисунок 5 – Вспомогательная модель цепи для постоянных значений при действии источников постоянных сигналов
В результате модель цепи будет имеет 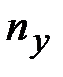 =2 узла,
=2 узла,  =3 ветвей,
=3 ветвей,  ;
;
 =
= 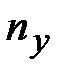 – 1 = 1 уравнения по первому закону Кирхгофа;
– 1 = 1 уравнения по первому закону Кирхгофа;
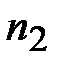 =
= 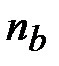 –
–  -
- 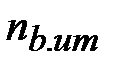 = 1 уравнения по второму закону Кирхгофа.
= 1 уравнения по второму закону Кирхгофа.
Количество уравнений должно быть равно количеству неизвестных токов:
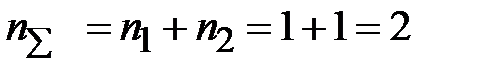
Выбираем узел и составляем уравнение по первому закону Кирхгофа:
Узел 1: 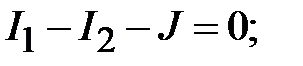
Для элементарного контура составляем уравнение по второму закону Кирхгофа:
1к: 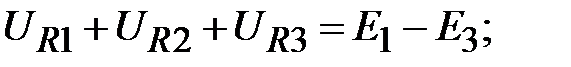
Преобразуем уравнения по второму закону Кирхгофа:
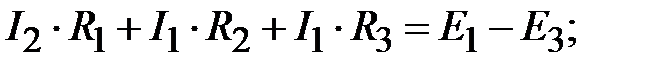
Полученная система уравнений имеет следующий вид:
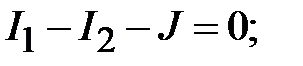
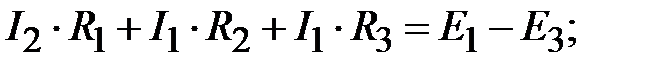
Уравнения баланса мощности для комплексных значений
Для записи уравнений баланса вырабатываемой и потребляемой комплексной мощности воспользуемся рисунком 3:
Вырабатываемая комплексная мощность:
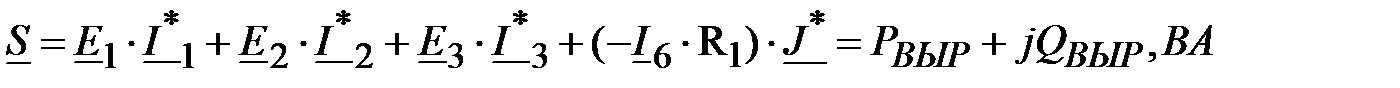
Потребляемая активная мощность:
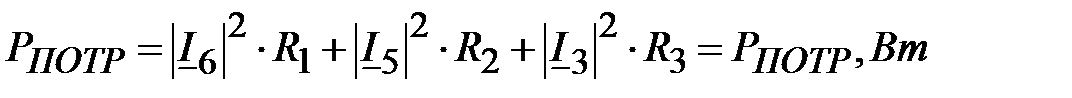
Потребляемая активная мощность:
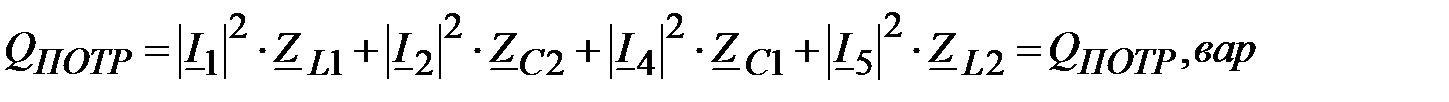
При правильном расчете токов и напряжений в модели цепи потребляемая и вырабатываемая мощность должны быть равны, т.е. баланс должен сойтись.