1. Пользуясь определением двойного интеграла, доказать, что
 ,
,
если  и
и 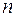 - натуральные числа, и, по меньшей мере, одно из них нечетно.
- натуральные числа, и, по меньшей мере, одно из них нечетно.
2. С помощью теоремы о среднем найти
 ,
,
где 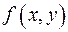 - непрерывная функция.
- непрерывная функция.
3. Оценить интеграл
 ,
,
т.е. указать, между какими значениями заключена его величина.
4. Вычислить двойной интеграл
 ,
,
если область  - прямоугольник {
- прямоугольник {  }, а
}, а 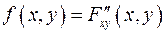 .
.
5. Доказать равенство
 б
б
если область  - прямоугольник {
- прямоугольник {  }.
}.
6. Доказать формулу Дирихле
 ,
,  .
.
7. Пользуясь формулой Дирихле, доказать равенство
 .
.
8. Какой из интегралов больше
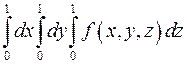 или
или 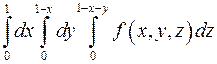 ,
,
если  ?
?
Расчетные задания
Задача 1. Изменить порядок интегрирования.
1.1.  . 1.2.
. 1.2.  .
.
1.3.  . 1.4.
. 1.4.  .
.
1.5.  . 1.6.
. 1.6.  .
.
1.7.  . 1.8.
. 1.8.  .
.
1.9. 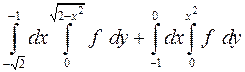 . 1.10.
. 1.10.  .
.
1.11.  . 1.12.
. 1.12.  .
.
1.13.  . 1.14.
. 1.14.  .
.
1.15.  . 1.16.
. 1.16.  .
.
1.17.  . 1.18.
. 1.18.  .
.
1.19.  . 1.20.
. 1.20. 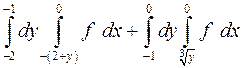 .
.
1.21. 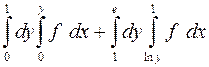 . 1.22.
. 1.22.  .
.
1.23.  . 1.24.
. 1.24.  .
.
1.25.  . 1.26.
. 1.26.  .
.
1.27.  . 1.28.
. 1.28.  .
.
1.29.  . 1.30.
. 1.30. 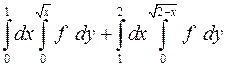 .
.
1.31.  .
.
Задача 2. Вычислить.
2.1. 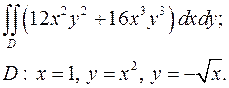 2.2.
2.2. 
2.3.  2.4.
2.4. 
2.5.  2.6.
2.6. 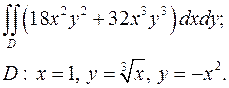
2.7.  2.8.
2.8. 
2.9.  2.10.
2.10. 
2.11.  2.12.
2.12. 
2.13.  2.14.
2.14. 
2.15.  2.16.
2.16. 
2.17. 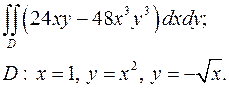 2.18.
2.18. 
2.19.  2.20.
2.20. 
2.21.  2.22.
2.22. 
2.23.  2.24.
2.24. 
2.25.  2.26.
2.26. 
2.27.  2.28.
2.28. 
2.29.  2.30.
2.30. 
2.31. 
Задача 3. Вычислить.
3.1.  3.2.
3.2. 
3.3.  3.4.
3.4. 
3.5.  3.6.
3.6. 
3.7.  3.8.
3.8. 
3.9.  3.10.
3.10. 
3.11.  3.12.
3.12. 
3.13. 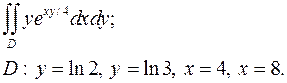 3.14.
3.14. 
3.15.  3.16.
3.16. 
3.17. 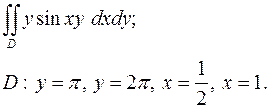 3.18.
3.18. 
3.19.  3.20.
3.20. 
3.21.  3.22.
3.22. 
3.23.  3.24.
3.24. 
3.25.  3.26.
3.26. 
3.27.  3.28.
3.28. 
3.29.  3.30.
3.30. 
3.31. 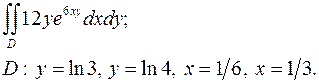
Задача 4. Вычислить.
4.1.  4.2.
4.2. 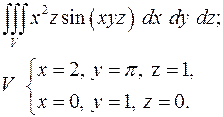
4.3.  4.4.
4.4. 
4.5.  4.6.
4.6. 
4.7.  4.8.
4.8. 
4.9.  4.10.
4.10. 
4.11.  4.12.
4.12. 
4.13.  4.14.
4.14. 
4.15.  4.16.
4.16. 
4.17.  4.18.
4.18. 
4.19. 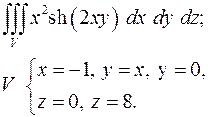 4.20.
4.20. 
4.21.  4.22.
4.22. 
4.23.  4.24.
4.24. 
4.25. 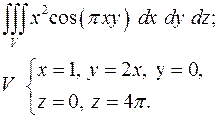 4.26.
4.26. 
4.27.  4.28.
4.28. 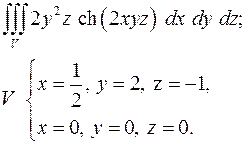
4.29. 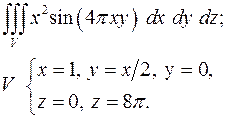 4.30.
4.30. 
4.31. 
Задача 5. Вычислить.
5.1.  5.2.
5.2. 
5.3.  5.4.
5.4. 
5.5.  5.6.
5.6. 
5.7. 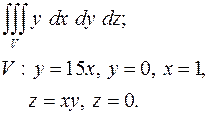 5.8.
5.8. 
5.9.  5.10.
5.10. 
5.11.  5.12.
5.12. 
5.13.  5.14.
5.14. 
5.15. 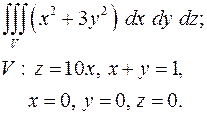 5.16.
5.16. 
5.17.  5.18.
5.18. 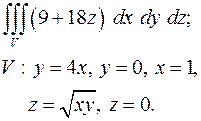
5.19.  5.20.
5.20. 
5.21.  5.22.
5.22. 
5.23.  5.24.
5.24. 
5.25.  5.26.
5.26. 
5.27.  5.28.
5.28. 
5.29.  5.30.
5.30. 
5.31. 
Задача 6. Найти площадь фигуры, ограниченной данными линиями.
6.1. 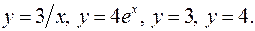
6.2. 
6.3. 
6.4. 
6.5. 
6.6. 
6.7. 
6.8. 
6.9. 
6.10. 
6.11. 
6.12. 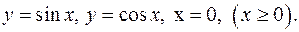
6.13. 
6.14. 
6.15. 
6.16. 
6.17. 
6.18. 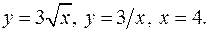
6.19. 
6.20. 
6.21. 
6.22. 
6.23. 
6.24. 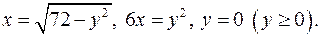
6.25. 
6.26. 
6.27. 
6.28. 
6.29. 
6.30. 
6.31. 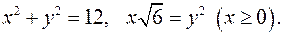
Задача 7. Найти площадь фигуры, ограниченной данными линиями.
7.1.  7.2.
7.2. 
7.3.  7.4.
7.4. 
7.5.  7.6.
7.6. 
7.7.  7.8.
7.8. 
7.9.  7.10.
7.10. 
7.11. 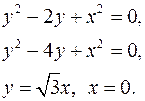 7.12.
7.12. 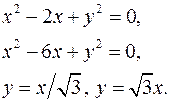
7.13.  7.14.
7.14. 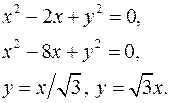
7.15. 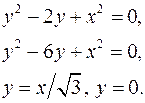 7.16.
7.16. 
7.17.  7.18.
7.18. 
7.19.  7.20.
7.20. 
7.21.  7.22.
7.22. 
7.23.  7.24.
7.24. 
7.25. 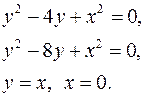 7.26.
7.26. 
7.27.  7.28.
7.28. 
7.29. 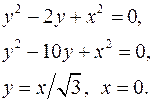 7.30.
7.30. 
7.31. 
Задача 8. Пластинка  задана ограничивающими ее кривыми,
задана ограничивающими ее кривыми,  - поверхностная плотность. Найти массу пластинки.
- поверхностная плотность. Найти массу пластинки.
8.1.  8.2.
8.2. 
8.3.  8.4.
8.4. 
8.5.  8.6.
8.6. 
8.7.  8.8.
8.8. 
8.9.  8.10.
8.10. 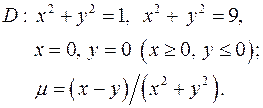
8.11.  8.12.
8.12. 
8.13.  8.14.
8.14. 
8.15.  8.16.
8.16. 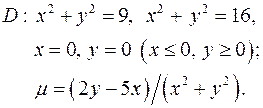
8.17.  8.18.
8.18. 
8.19.  8.20.
8.20. 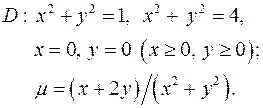
8.21.  8.22.
8.22. 
8.23. 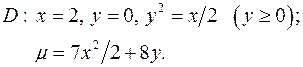 8.24.
8.24. 
8.25.  8.26.
8.26. 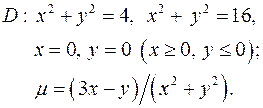
8.27.  8.28.
8.28. 
8.29. 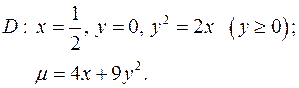 8.30.
8.30. 
8.31. 
Задача 9. Пластинка D задана неравенствами, m - поверхностная плотность. Найти массу пластинки.
9.1.  9.2.
9.2. 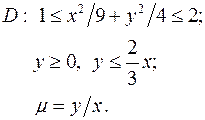
9.3.  9.4.
9.4. 
9.5. 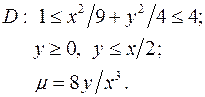 9.6.
9.6. 
9.7. 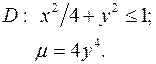 9.8.
9.8. 
9.9.  9.10.
9.10. 
9.11.  9.12.
9.12. 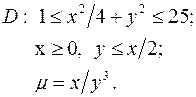
9.13.  9.14.
9.14. 
9.15.  9.16.
9.16. 
9.17.  9.18.
9.18. 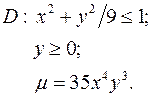
9.19. 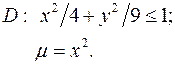 9.20.
9.20. 
9.21.  9.22.
9.22. 
9.23.  9.24.
9.24. 
9.25.  9.26.
9.26. 
9.27.  9.28.
9.28. 
9.29.  9.30.
9.30. 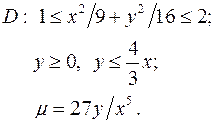
9.31. 
Задача 10. Найти объем тела, заданного ограничивающими его поверхностями.
10.1. 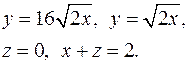 10.2.
10.2. 
10.3.  10.4.
10.4. 
10.5.  10.6.
10.6. 
10.7.  10.8.
10.8. 
10.9. 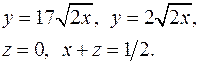 10.10.
10.10. 
10.11.  10.12.
10.12. 
10.13.  10.14.
10.14. 
10.15. 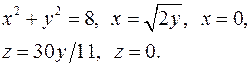 10.16.
10.16. 
10.17. 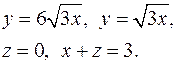 10.18.
10.18. 
10.19. 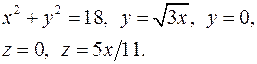 10.20.
10.20. 
10.21.  10.22.
10.22. 
10.23.  10.24.
10.24. 
10.25. 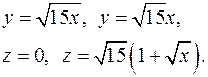 10.26.
10.26. 
10.27.  10.28.
10.28. 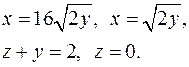
10.29.  10.30.
10.30. 
10.31. 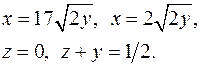
Задача 11. Найти объем тела, заданного ограничивающими его поверхностями.
11.1.  11.2.
11.2. 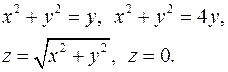
11.3.  11.4.
11.4. 
11.5.  11.6.
11.6. 
11.7. 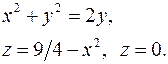 11.8.
11.8. 
11.9. 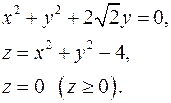 11.10.
11.10. 
11.11.  11.12.
11.12. 
11.13. 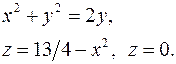 11.14.
11.14. 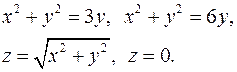
11.15.  11.16.
11.16. 
11.17.  11.18.
11.18. 
11.19. 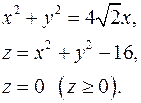 11.20.
11.20. 
11.21.  11.22.
11.22. 
11.23.  11.24.
11.24. 
11.25.  11.26.
11.26. 
11.27.  11.28.
11.28. 
11.29.  11.30.
11.30. 
11.31. 
Задача 12. Найти объем тела, заданного ограничивающими его поверхностями.
12.1.  12.2.
12.2. 
12.3.  12.4.
12.4. 
12.5.  12.6.
12.6. 
12.7.  12.8.
12.8. 
12.9.  12.10.
12.10. 
12.11.  12.12.
12.12. 
12.13. 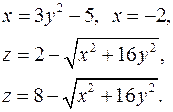 12.14.
12.14. 
12.15.  12.16.
12.16. 
12.17.  12.18.
12.18. 
12.19.  12.20.
12.20. 
12.21.  12.22.
12.22. 
12.23.  12.24.
12.24. 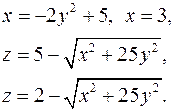
12.25.  12.26.
12.26. 
12.27.  12.28.
12.28. 
12.29.  12.30.
12.30. 
12.31. 
Задача 13. Найти объем тела, заданного ограничивающими его поверхностями.
13.1.  13.2.
13.2. 
13.3.  13.4.
13.4. 
13.5.  13.6.
13.6. 
13.7. 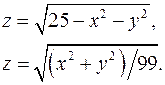 13.8.
13.8. 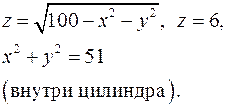
13.9.  13.10.
13.10. 
13.11. 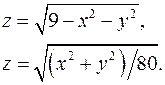 13.12.
13.12. 
13.13. 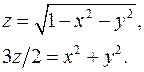 13.14.
13.14. 
13.15.  13.16.
13.16. 
13.17.  13.18.
13.18. 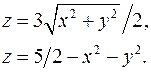
13.19.  13.20.
13.20. 
13.21.  13.22.
13.22. 
13.23.  13.24.
13.24. 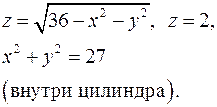
13.25.  13.26.
13.26. 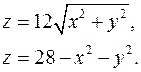
13.27.  13.28.
13.28. 
13.29. 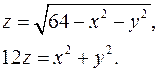 13.30.
13.30. 
13.31. 
Задача 14. Найти объем тела, заданного ограничивающими его поверхностями.
14.1. 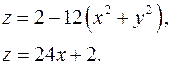 14.2.
14.2. 
14.3.  14.4.
14.4. 
14.5.  14.6.
14.6. 
14.7.  14.8.
14.8. 
14.9. 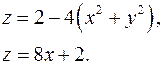 14.10.
14.10. 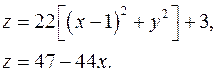
14.11.  14.12.
14.12. 
14.13.  14.14.
14.14. 
14.15. 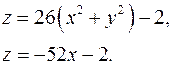 14.16.
14.16. 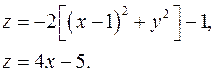
14.17.  14.18.
14.18. 
14.19.  14.20.
14.20. 
14.21.  14.22.
14.22. 
14.23.  14.24.
14.24. 
14.25.  14.26.
14.26. 
14.27.  14.28.
14.28. 
14.29.  14.30.
14.30. 
14.31. 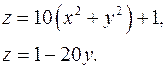
Задача 15. Найти объем тела, заданного неравенствами.
15.1.  15.2.
15.2. 
15.3.  15.4.
15.4. 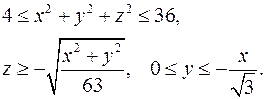
15.5.  15.6.
15.6. 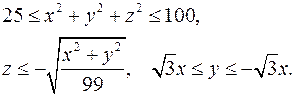
15.7.  15.8.
15.8. 
15.9. 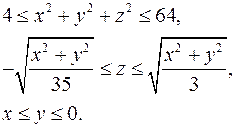 15.10.
15.10. 
15.11.  15.12.
15.12. 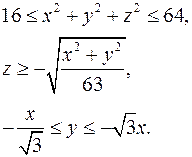
15.13.  15.14.
15.14. 
15.15.  15.16.
15.16. 
15.17.  15.18.
15.18. 
15.19.  15.20.
15.20. 
15.21.  15.22.
15.22. 
15.23.  15.24.
15.24. 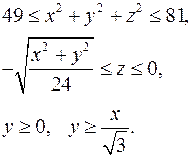
15.25.  15.26.
15.26. 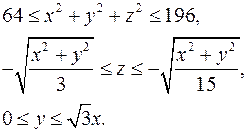
15.27.  15.28.
15.28. 
15.29.  15.30.
15.30. 
15.31. 
Задача 16. Тело V задано ограничивающими его поверхностями, m - плотность. Найти массу тела.
16.1. 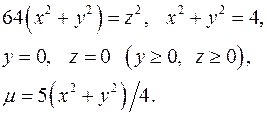
16.2. 
16.3. 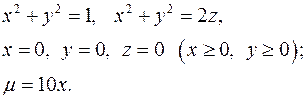
16.4. 
16.5. 
16.6. 
16.7. 
16.8. 
16.9. 
16.10. 
16.11. 
16.12. 
16.13. 
16.14. 
16.15. 
16.16. 
16.17. 
16.18. 
16.19. 
16.20. 
16.21. 
16.22. 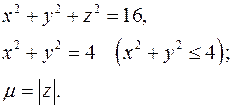
16.23. 
16.24. 
16.25. 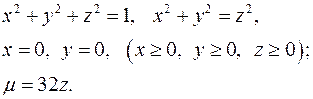
16.26. 
16.27. 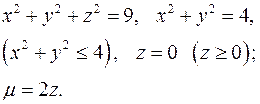
16.28. 
16.29. 
16.30. 
16.31. 
VIII. ВЕКТОРНЫЙ АНАЛИЗ
Теоретические вопросы
1. Скалярное поле. Производная по направлению.
2. Градиент, его свойства. Инвариантное определение градиента.
3. Векторное поле. Поток векторного поля через поверхность, его физический смысл.
4. Формула Остроградского.
5. Дивергенция векторного поля, ее физический смысл. Инвариантное определение дивергенции. Свойства дивергенции.
6. Соленоидальное поле, его основные свойства.
7. Линейный интеграл в векторном поле, его свойства и физический смысл.
8. Циркуляция векторного поля, ее гидродинамический смысл.
9. Формула Стокса.
10. Ротор векторного поля, его свойства. Инвариантное определение ротора.
11. Условия независимости линейного интеграла от формы пути интегрирования.
12. Потенциальное поле. Условия потенциальности.