Т2. Определители квадратных матриц и их свойства.
Каждой квадратной матрице поставим в соответствие число, которое назовём определителем или детерминантом матрицы. Определитель матрицы 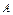 обозначают
обозначают 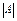 ,или
,или 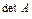 , или
, или 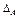 .
.
Определитель матрицы – число, равное алгебраической сумме всех произведений её элементов, взятых по одному из каждой строки и каждого столбца.
Знак произведения определяется расположением вторых индексов его элементов.
Число множителей в каждом произведении равно 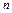 , а число этих произведений
, а число этих произведений 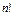 =
= 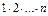 .
.
Определитель матрицы второго порядка – число, равное разности произведения элементов главной диагонали матрицы и произведения элементов побочной диагонали матрицы.
Т.е., если 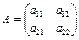 , то
, то 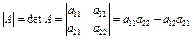
Определитель матрицы третьего порядка – число, вычисляемое по формуле:
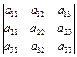 =
= 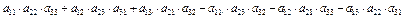
Способы вычисления определителя третьего порядка: метод треугольников и правило Саррюса.
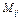 - минор первого порядка, равный определителю матрицы (n-1)-го порядка, состоящей из всех строк и столбцов матрицы А, за исключением i-ой строки и j – го столбца этой матрицы.
- минор первого порядка, равный определителю матрицы (n-1)-го порядка, состоящей из всех строк и столбцов матрицы А, за исключением i-ой строки и j – го столбца этой матрицы.
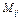 - дополнительный минор для элемента
- дополнительный минор для элемента 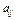 матрицы А.
матрицы А.
Алгебраическое дополнение 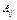 элемента
элемента 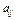 матрицы А –число, равное дополнительному минору этого элемента, взятого со знаком «+», если (
матрицы А –число, равное дополнительному минору этого элемента, взятого со знаком «+», если (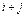 ) - чётное, или со знаком «-», если (
) - чётное, или со знаком «-», если (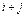 ) – нечётно.
) – нечётно.
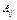 = = 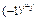 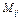
|
Разложение определителей по элементам ряда.
Определитель любой матрицы можно вычислить как сумму произведений элементов какого – либо ряда матрицы (её строки или столбца) на их алгебраические дополнения.
Например, 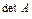 =
= 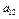
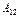 +
+ 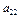
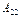 +
+ 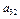
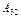 +
+ 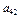
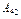 - разложение определителя матрицы четвёртого порядка по элементам её второго столбца, а
- разложение определителя матрицы четвёртого порядка по элементам её второго столбца, а 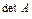 =
= 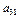
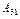 +
+ 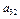
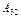 +
+ 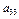
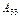 +
+ 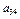
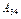 - разложение определителя той же матрицы по элементам третьей строки.
- разложение определителя той же матрицы по элементам третьей строки.
Определитель третьего порядка также можно вычислить, представив его как сумму трёх определителей второго порядка, например, разложив его по элементам первого столбца:
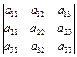 =
= 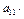 (-1)
(-1) 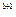
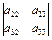 +
+ 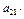 (-1)
(-1) 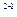
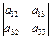 +
+ 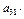 (-1)
(-1) 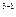
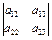 .
.
Свойства определителей квадратных матриц.
1. Если строка (столбец) матрицы состоит из одних нулей, то её определитель равен нулю.
2. Определитель матрицы с двумя одинаковыми строками (столбцами) равен нулю.
3. Если все элементы строки (столбца) определителя содержат общий множитель, то его можно вынести за знак определителя.
4. Следствие из 2 и 3 свойства: определитель, содержащий два ряда, соответствующие элементы которых пропорциональны друг другу, равен нулю.
5. Если два определителя отличаются друг от друга только элементами одного какого-либо ряда, то их сумма равна такому же определителю, в котором вместо отличающихся друг от друга рядов определителей помещён ряд, составленный из сумм элементов этих рядов.
6. Значение определителя не изменится, если к элементам любого его ряда прибавить соответствующие элементы другого ряда, умноженные на произвольное число.
7. Определитель матрицы равен нулю тогда и только тогда, когда её строки (столбцы) линейно зависимы.
8. При перестановке двух строк (столбцов) матрицы, её определитель меняет знак на противоположный.
9. При транспонировании матриц её определитель не меняется.
10. Определитель равен сумме произведений элементов какого – либо ряда на их алгебраические дополнения.
11. Сумма произведений элементов какого – либо ряда на алгебраические дополнения элементов другого ряда равна нулю.
12. Если в определители все элементы какого-либо ряда кроме одного равны нулю, то определитель равен произведению этого элемента на его алгебраическое дополнение.
13. Определители диагональной и треугольной матрицы равны произведению элементов главной диагонали этих матриц.
Ранг матрицы.
Ранг матрицы – число r, равное максимальному числу линейно независимых векторов-строк или векторов -столбцов этой матрицы.
Невырожденная матрица - квадратная матрица n-го порядка, ранг которой равен её порядку. (n=r).