Задание на курсовой проект
Построить математическую модель системы автоматического регулирования расхода пара. Кран с электроприводом.
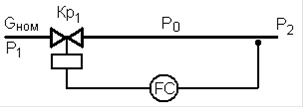
Рисунок 1 - Объект регулирования
Заданные значения:
заданное значение давления после крана -P0 = 1 МПа;
температура рабочей среды до крана -U = 303 8К;
номинальный расход рабочей среды -G = 3.5 кг/с;
номинальное давление до крана -Р1 = 1.3 МПа.
Введение
Химическое производство состоит из целого ряда взаимосвязанных единичных процессов химической технологии и представляет собой сложную систему, характеризующуюся большим объемом информации. Изучение и разработка химико-технологической системы направлены на создание высокопродуктивных, высококачественных и экономических производств и в настоящее время ведутся на основе метода математического моделирования.
Моделирование - метод экспериментально-теоретического исследования сложных систем, позволяющий в качестве объекта рассматривать не подлинное явление, а некую его модель. Под моделью подразумевается такая упрощенная система, которая отражает совокупность свойств объекта, соответствующих представленной задаче моделирования, и дает возможность получить новые сведения об объекте.
В частности по математической моделью химико-технологического процесса следует понимать совокупность качественных представлений и математических соотношений, характеризующих отдельные, ограниченные в нужном направлении явления моделируемого процесса, а также взаимодействию этих явлений с учетом возмущающих факторов. Математические соотношения, составленные в результате теоретического анализа моделируемого процесса, представляют собой математическое описание.
Изучение объекта моделирования (химико-технологического процесса, отдельного аппарата, физико-химического явления и т.д.) сводится к анализу его математического описания в явном виде, т.е. к анализу зависимостей между определяющими и определяемыми переменными процесса. Эти зависимости можно получить только в результате решения уравнений математического описания. Для решения даже относительно простого математического описания, не говоря уже о сложных математических моделях, обычно требуются большие объемы вычислительных операций. Поэтому практическая реализация математических моделей невозможна без современных средств вычислительной техники.
Содержательное описание объекта регулирования
Имеется участок трубопровода по которому осуществляется подача пара.

Рисунок 2 - Трубопровод с участком регулирования расхода
Объект регулирования - участок трубопровода от измерительного устройства до регулирующего органа.
Рабочее тело - перегретый пар (удельный вес γ=(9,81*10,83)=106,24, [Н/м3]).
Регулируемый параметр - расход пара 1,477 м3/с.
Заданные значения:
заданное значение давления после крана -P0 = 1 МПа;
температура рабочей среды до крана -U = 303 8К;
номинальный расход рабочей среды -G = 3.5 кг/с;
номинальное давление до крана -Р1 = 1.3 МПа.
Аналитическое описание модели объекта регулирования
Для составления аналитической модели, необходимо:
определить время разгона объекта;
определить коэффициент самовыравнивания на линиях притока и оттока. Объект регулирование будем рассматривать как типовой одноемкостной объект, динамика которого может быть описана дифференциальным уравнением 1-го порядка:
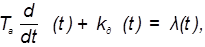 (1)
(1)
где Ta - время разгона, с; кд - степень самовыравнивания; l(t) - относительная величина возмущающего воздействия; j(t) - относительная величина регулируемого параметра.
Относительная величина возмущающего воздействия
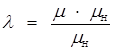 (2)
(2)
Относительная величина регулируемого параметра
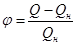 (3)
(3)
Степень самовыравнивания кд=1, т. к. расход на притоке равен расходу на оттоке.
Время разгона объекта
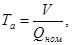 (4)
(4)
где Qн - номинальный расход, м3/с; V - объем участка трубопровода, м3.
Номинальный расход
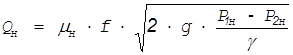 (5)
(5)
где  - площадь сечения трубопровода, м2.
- площадь сечения трубопровода, м2.
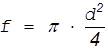 (6)
(6)
Подставив численные значения, найдем

Объем участка трубопровода
 (7)
(7)
Время разгона
 (8)
(8)
В данном случае коэффициент самовыравнивания 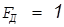 , т.к.
, т.к. 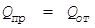
Тогда дифференциальное уравнение, описывающее объект:
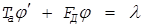 ,(9)
,(9)
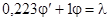 ,
,
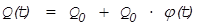 (10)
(10)
Тогда дифференциальное уравнение, описывающее объект во временных координатах, будет иметь вид
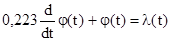 .(11)
.(11)
Приведем уравнение к канонической форме (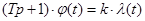 ):
):
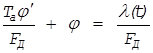 ,(12)
,(12)
где - 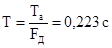 ,
, 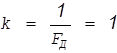
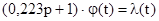
Запишем передаточную функцию объекта
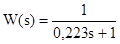 (13)
(13)