ВАРИАНТЫКОНТРОЛЬНОЙ РАБОТЫ
По дисциплине «Математический анализ и
Линейная алгебра»
для слушателей факультета непрерывного обучения
Ниже приводятся только варианты контрольных работ по данной дисциплине и указания по их выполнению, взятые из пособия: Математический анализ и линейная алгебра. Учебно-методическое пособие для слушателей факультета непрерывного обучения / Под ред. проф. Н.Ш. Кремера. – М.: ВЗФЭИ, 2010.
Полностью указанное пособие приводится в Интернет-репозитории института (https://repository.vzfei.ru). В этом пособии, кроме приведенных здесь вариантов контрольных работ и указаний по их выполнению, представлены методические рекомендации по изучению дисциплины, типовые задачи (с решениями и для самоподготовки) и вопросы для самопроверки.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
В соответствии с учебным планом по дисциплине «Математический анализ и линейная алгебра» каждый студент должен выполнить две домашние контрольные работы № 1 и № 2 (по приведенным в данной брошюре вариантам) в сроки, установленные учебным графиком.
По каждой контрольной работе и студенты вечерних и дневных групп проходят собеседование. На собеседовании выясняется, насколько глубоко усвоен пройденный материал и соответствуют ли знания студента и его навыки в решении задач качеству представленной работы. Зачет по каждой контрольной работе студенты получают лишь успешного прохождения собеседования.
Номер варианта контрольной работы определяется по последней цифре номера личного дела студента, который совпадает с номером его зачетной книжки и студенческого билета.
Сроки представления домашних контрольных работ на проверку указаны в индивидуальном графике студента, а также сообщаются во время осенней установочной сессии. Однако эти сроки являются крайними. Чтобы работа была своевременно проверена, а при необходимости доработана и сдана повторно, ее надлежит представить значительно раньше указанного срока. Студентам дневных групп рекомендуется свои домашние контрольные работы выполнять во время сессии (контрольную работу № 1 – во время осенней установочной, № 2 – во время зимней экзаменационной). Это даст возможность студенту использовать свое пребывание в институте для консультаций по всем возникшим при выполнении работы вопросам. После окончания сессии в течение двух недель работу необходимо окончательно завершить, а затем представить на проверку.
|
|
Если в ходе написания работы у студента появятся вопросы или затруднения в решении задач контрольного задания, он может обратиться в институт за устной или письменной консультацией (например, по электронной почте на форум кафедры).
При изучении учебного материала и подготовке к контрольным работам рекомендуется использовать учебники и учебные пособия, Интернет-ресурсы, приведенные выше в разделе «Литература», а также данную брошюру.
После проверки контрольная работа студента получает оценку «Допускается к собеседованию» или «Не допускается к собеседованию».
Каждая контрольная работа содержит набор заданий, при выполнении которых необходимо соблюдать следующие правила.
1. Работа должна быть выполнена в школьной тетради, имеющей широкие (не менее 3 см) поля для замечаний рецензента.
|
|
2. Перед решением каждой задачи нужно привести полностью ее условие.
3. Следует придерживаться той последовательности при решении задач, в какой они даны в задании, строго сохраняя при этом нумерацию примеров (задач).
4. Не допускается замена задач контрольного задания другими.
5. Решения задач должны сопровождаться развернутыми пояснениями, нужно привести в общем виде используемые формулы с объяснением употребляемых обозначений, а окончательный ответ следует выделить.
6. Чертежи к задачам № 5, 6 контрольных работ № 1 и 2 должны быть выполнены в прямоугольной системе координат в полном соответствии с данными условиями задач и теми результатами, которые получены.
7. В конце работы приводится список использованной литературы (указывают автора, название, издательство, год издания), ставится дата окончания работы и подпись.
8. Если вычисления, выполняемые при решении задач, приближенные, то следует придерживаться правил приближенных вычислений, которые приведены в данном учебно-методическом пособии.
9. На обложке тетради следует указать фамилию, имя, отчество (полностью), факультет, специальность, курс, номер личного дела, вариант и номер контрольной работы, место работы, занимаемую должность и точный домашний адрес.
Если работа получила в целом положительную оценку («Допускается к собеседованию»), но в ней есть отдельные недочеты (указанные в тетради), то нужно сделать соответствующие исправления и дополнения в той же тетради (после имеющихся решений и записи «Работа над ошибками») и предъявить доработку на собеседовании. Если работа «не допускается к собеседованию», ее необходимо в соответствии с требованиями преподавателя частично или полностью переделать. Повторную работу надо выполнить в той же тетради (если есть место) или в новой с надписью на обложке «Повторная», указав фамилию преподавателя, которым работа была ранее не зачтена. Вместе с незачтенной работой и рецензией повторную работу направить снова в институт.
|
|
Контрольная работа не зачитывается, если ее вариант не совпадает с последней цифрой номера личного дела студента или она выполнена по вариантам прошлых лет.
Студенты, не получившие зачета хотя бы по одной из двух контрольных работ, к экзамену не допускаются. Зачтенные работы предъявляются на экзамене и не подлежат возвращению после успешной сдачи экзамена.
ВАРИАНТЫКОНТРОЛЬНЫХ РАБОТ [1]
ВАРИАНТ 1
(для студентов, номера личных дел которых
Оканчиваются цифрой 1)
Контрольная работа №1
1. Найти ранг матрицы:
.
2. Найти предел:
3. Найти производную функции:
4. Найти два положительных числа, сумма которых равна 6, а сумма их кубов является наименьшей.
5. Составить уравнение касательных к графику функции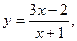 
параллельных прямой, проходящей через точки (1; 8) и (–1; –2). Сделать чертеж.
6. Исследовать функцию 
и построить схематично ее график.
Контрольная работа № 2
1. Найти неопределенный интеграл:
Вычислить определенные интегралы:
2. 
3. 
4. Решить дифференциальное уравнение:
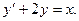
5. Вычислить площадь фигуры, ограниченной линиями:
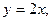
6. Экспериментальные данные о значениях переменных х и y приведены в таблице:
| 1,5 | 2,5 | 3,5 | |||
|
В результате их выравнивания получена функция 
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью 
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
7. Вычислить приближенно определенный интеграл
взяв три члена разложения подынтегральной функции в ряд Маклорена. Оценить погрешность.
ВАРИАНТ 2
(для студентов, номера личных дел которых
Оканчиваются цифрой 2)
Контрольная работа №1
1. По формулам Крамера решить систему линейных уравнений:
2. Найти предел:
3. Найти производную функции:
4. Какую наибольшую площадь может иметь прямоугольный треугольник, сумма квадратов катетов которого равна 18?
5. Составить уравнения касательных к графику функции 
проведенных в точках ее пересечения с прямой 
Сделать чертеж.
6. Исследовать функцию 
и построить схематично ее график.
Контрольная работа № 2
1. Найти неопределенный интеграл:
Вычислить определенные интегралы:
2. 
3. 
4. Решить дифференциальное уравнение:
5. Вычислить площадь фигуры, ограниченной линиями:
6. Экспериментальные данные о значениях переменных х и y приведены в таблице:
| |||||
|
В результате их выравнивания получена функция 
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
7. Найти область сходимости степенного ряда:
ВАРИАНТ 3
(для студентов, номера личных дел которых
Оканчиваются цифрой 3)
Контрольная работа №1
1. Методом обратной матрицы решить систему линейных уравнений:
2. Найти предел:
3. Найти производную функции:
4. Внутреннюю поверхность резервуара емкостью 4 м3 с квадратным основанием, открытого сверху, нужно покрыть оловом. Каковы должны быть размеры резервуара, чтобы расход олова оказался минимальным. (Толщиной стенок пренебречь).
5. Составить уравнения касательных к графику функции 
образующих с осью Ох угол 
. Сделать чертеж.
6. Исследовать функцию 
и построить схематично ее график.
Контрольная работа № 2
1. Найти неопределенный интеграл:
Вычислить определенные интегралы:
2. 
3. 
4. Решить дифференциальное уравнение:
5. Вычислить площадь фигуры, ограниченной линиями:
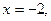
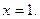
6. Экспериментальные данные о значениях переменных х и y приведены в таблице:
| ||||||
|
| 1,3 | 1,8 | 2,2 | 2,3 | 2,6 |
В результате их выравнивания получена функция 
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью 
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
7. Используя разложение функции 
в степенной ряд, вычислить ln 1,12 с точностью до 0,001.
ВАРИАНТ 4
(для студентов, номера личных дел которых
Оканчиваются цифрой 4)
Контрольная работа №1
1. Методом Гаусса решить систему линейных уравнений:
2. Найти предел:
3. Найти производную функции:
4. Под посевы элитных культур выделили земельный участок прямоугольной формы площадью 324 м2 и вдоль всей границы окопали рвом. Найти такие длину и ширину участка, при которых стоимость рва является наименьшей.
5. Составить уравнения касательных к графику функции 
, перпендикулярных прямой, проходящей через точки (1; 1) и (–1; 0). Сделать чертеж.
6. Исследовать функцию 
и схематично построить ее график.
Контрольная работа № 2
1. Найти неопределенный интеграл:
Вычислить определенные интегралы:
2. 
3. 
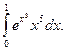
4. Решить дифференциальное уравнение:
5. Вычислить площадь фигуры, ограниченной линиями:
6. Экспериментальные данные о значениях переменных х и y приведены в таблице:
| 4,5 | 5,5 | |||
| 0,8 | 0,5 | 0,2 | 0,4 | 0,9 |
В результате их выравнивания получена функция 
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью 
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
7. Найти область сходимости степенного ряда:
ВАРИАНТ 5
(для студентов, номера личных дел которых
Оканчиваются цифрой 5)
Контрольная работа №1
1. Решить матричное уравнение 
, где 
.
2. Найти предел:
3. Найти производную функции:
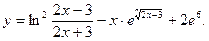
4. Из всех прямоугольных участков с диагональю 8 дм найти размеры участка, имеющего наибольшую площадь.
5. Хорда параболы 
соединяет точки с абсциссами 
и 
. Составить уравнение касательной к параболе, параллельной этой хорде. Сделать чертеж.
6. Исследовать функцию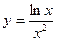 
и построить схематично ее график.
Контрольная работа № 2
1. Найти неопределенный интеграл:
Вычислить определенные интегралы:
2. 
3. 
4. Решить дифференциальное уравнение:
5. Вычислить площадь фигуры, ограниченной линиями:
6. Экспериментальные данные о значениях переменных х и y приведены в таблице:
| –2 | –1 | |||
| 0,5 | 0,2 |
В результате их выравнивания получена функция 
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
7. Найти область сходимости степенного ряда:
ВАРИАНТ 6
(для студентов, номера личных дел которых
оканчиваются цифрой 6)
Контрольная работа №1
1. Найти ранг матрицы 
, где 
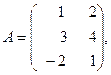
2. Найти предел:
3. Найти производную функции:
4. Требуется изготовить ящик с крышкой, объем которого 1800 дм3, а стороны основания относятся как 2:3. Каковы должны быть размеры ящика, чтобы расход материала оказался наименьшим?
5. Составить уравнения касательных к графику функции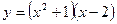 
в точках ее пересечения с осями координат. Сделать чертеж.
6. Исследовать функцию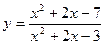 
и построить схематично ее график.
Контрольная работа № 2
1. Найти неопределенный интеграл:
Вычислить определенные интегралы:
2. 
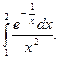
3. 
4. Решить дифференциальное уравнение:
5. Вычислить площадь фигуры, ограниченной линиями:
6. Экспериментальные данные о значениях переменных х и y приведены в таблице:
| –4 | –3 | –2 | –1 | ||
|
| –1,2 | –0,71 | –0,01 | 0,53 | 0,82 | 0,92 |
В результате их выравнивания получена функция 
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью 
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
7. Исследовать ряд на сходимость:
В случае сходимости ряда установить ее характер (абсолютная или условная).
ВАРИАНТ 7
(для студентов, номера личных дел которых
оканчиваются цифрой 7)
Контрольная работа №1
1. По формулам Крамера решить систему линейных уравнений:
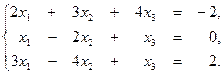
2. Найти предел:
3. Найти производную функции:
4. Число 49 представить в виде произведения двух положительных множителей, сумма квадратов которых является наименьшей.
5. Составить уравнение касательной к графику функции 
перпендикулярной прямой 
. Сделать чертеж.
6. Исследовать функцию 
и построить схематично ее график.
Контрольная работа № 2
1. Найти неопределенный интеграл:
Вычислить определенные интегралы:
2. 
3. 
4. Решить дифференциальное уравнение:
.
5. Вычислить площадь фигуры, ограниченной линиями:
6. Экспериментальные данные о значениях переменных х и y приведены в таблице:
|
| –3 | –2 | –1 | ||||
|
|
В результате их выравнивания получена функция 
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
7. Исследовать ряд на сходимость:
.
В случае сходимости ряда установить ее характер (абсолютная или условная).
ВАРИАНТ 8
(для студентов, номера личных дел которых
оканчиваются цифрой 8)
Контрольная работа №1
1. Методом обратной матрицы решить систему линейных уравнений:
2. Найти предел:
3. Найти производную функции:
4. Прямоугольный участок земли, примыкающий к стене заводского здания, нужно обнести забором. Часть забора, параллельная стене, должна быть каменной, а остальная часть – деревянной. Площадь участка – 90 м2. Стоимость 1 м каменного забора 10 тыс. руб., а 1 м. деревянного – 8 тыс. руб.
Найти такие размеры участка, чтобы стоимость забора была наименьшей. Какова эта стоимость?
5. Составить уравнения касательных к графику функции 
которые параллельны прямой 
. Сделать чертеж.
6. Исследовать функцию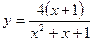 
и построить схематично ее график.
Контрольная работа № 2
1. Найти неопределенный интеграл:
Вычислить определенные интегралы:
2. 
3. 
4. Решить дифференциальное уравнение:
5. Вычислить площадь фигуры, ограниченной линиями:
6. Экспериментальные данные о значениях переменных х и y приведены в таблице:
| –3 | –1 | |||
| –1,3 | –2,6 | 3,3 | 0,8 | 0,8 |
В результате их выравнивания получена функция 
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью 
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
7. Используя разложение функции 
в степенной ряд, вычислить 
с точностью до 0,001.
ВАРИАНТ 9
(для студентов, номера личных дел которых
оканчиваются цифрой 9)
Контрольная работа №1
1. Методом Гаусса решить систему линейных уравнений:
2. Найти предел:
3. Найти производную функции:
4. Какова наибольшая площадь прямоугольного участка земли, который можно огородить забором, имеющим длину 56 м?
5. Составить уравнения касательных к графику функции 
в точках ее пересечения с прямой, проходящей через точки с координатами (1; 5) и (–1; –5). Сделать чертеж.
6. Исследовать функцию 
и построить схематично ее график.
Контрольная работа № 2
1. Найти неопределенный интеграл:
Вычислить определенные интегралы:
2. 
3. 
4. Решить дифференциальное уравнение:
5. Вычислить площадь фигуры, ограниченной линиями
6. Экспериментальные данные о значениях переменных х и y приведены в таблице:
|
| |||||
|
| 0,91 | 1,02 | 1,26 | 1,30 | 1,41 |
В результате их выравнивания получена функция 
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
7. Исследовать сходимость числового ряда:
ВАРИАНТ 10
(для студентов, номера личных дел которых
оканчиваются цифрой 0)
Контрольная работа №1
1. Найти матрицу 
, где
2. Найти предел:
3. Найти производную функции:
4. Требуется изготовить открытый цилиндрический бак емкостью 1000 см2. При каком радиусе основания на изготовление бака уйдет наименьшее количество материала?
5. Составить уравнения касательных к графику функции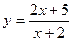 
, перпендикулярных прямой, проходящей через точки (0; 3) и (1; 7). Сделать чертеж.
6. Исследовать функцию 
и схематично построить ее график.
Контрольная работа № 2
1. Найти неопределенный интеграл:
Вычислить определенные интегралы:
2. 
3. 
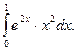
4. Решить дифференциальное уравнение:
5. Вычислить площадь фигуры, ограниченной линиями:
6. Экспериментальные данные о значениях переменных х и y приведены в таблице:
|
| 1,5 | 2,5 | |||
| 2,2 | 3,9 | 5,8 | 8,8 | 12,3 |
В результате их выравнивания получена функция 
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью 
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
7. Найти область сходимости степенного ряда:
[1] Для определения варианта, по которому надо выполнить контрольные работы №1 и 2, напоминаем, что номер личного дела студента совпадает с номером его зачетной книжки или студенческого билета